Graniastosłup Prosty O Podstawie Rombu

Drodzy nauczyciele matematyki! Ten artykuł poświęcony jest jednemu z fascynujących zagadnień geometrii przestrzennej – graniastosłupowi prostemu o podstawie rombu. Omówimy, jak w przystępny sposób wprowadzić ten temat na lekcjach, jakie pułapki czyhają na uczniów i jak uczynić naukę bardziej angażującą. Graniastosłup prosty o podstawie rombu to specyficzny typ graniastosłupa, który łączy w sobie cechy zarówno graniastosłupa prostego, jak i rombu, co stwarza ciekawe możliwości edukacyjne.

Definicja i Podstawowe Własności

Zacznijmy od podstaw. Graniastosłup prosty to bryła, której ściany boczne są prostokątami prostopadłymi do podstaw. W przypadku graniastosłupa prostego o podstawie rombu, podstawa jest rombem. Romby charakteryzują się tym, że mają wszystkie boki równe, ale kąty nie muszą być proste (w przeciwieństwie do kwadratu). Ważne jest, aby podkreślić tę różnicę już na początku. Uczniowie często mylą romb z kwadratem, co prowadzi do błędnych wniosków podczas obliczeń.

Podstawowe własności, które należy omówić z uczniami:

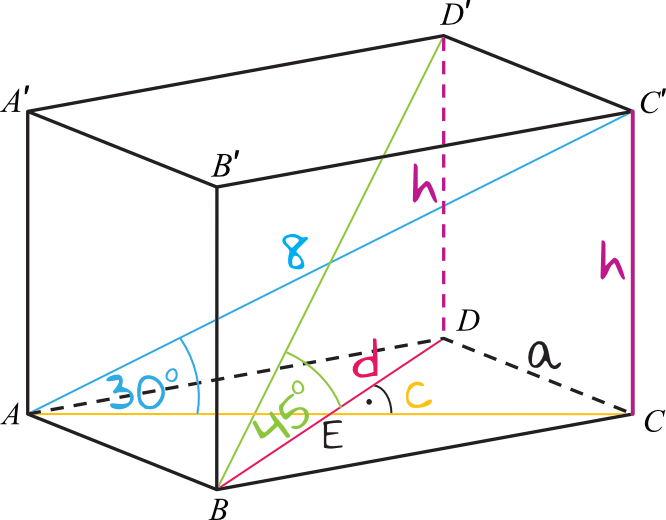
Podstawa: Romb (cztery boki równej długości, przekątne przecinają się pod kątem prostym i dzielą na połowy).
Ściany boczne: Prostokąty (prostopadłe do podstawy).
Wysokość: Odległość między podstawami (równa długości krawędzi bocznej).
Krawędzie: 8 wierzchołków i 12 krawędzi (4 krawędzie w podstawie, 4 w górnej podstawie i 4 krawędzie boczne).

Wprowadzenie Tematu w Klasie - Metody i Narzędzia

1. Rozpocznij od wizualizacji: Najlepszym sposobem na wprowadzenie nowego tematu jest pokazanie uczniom konkretnych modeli. Można wykorzystać gotowe modele graniastosłupów prostych o podstawie rombu, zbudować je samodzielnie z papieru lub kartonu, albo skorzystać z interaktywnych aplikacji i symulacji 3D.

2. Nawiąż do znanych brył: Porównaj graniastosłup prosty o podstawie rombu z innymi graniastosłupami prostymi, np. o podstawie kwadratu lub prostokąta. Podkreśl podobieństwa i różnice. Pokaż, że zmiana kształtu podstawy wpływa na własności całej bryły.

3. Rozbij na elementy: Rozłóż model graniastosłupa na poszczególne ściany (podstawy i ściany boczne). Uczniowie zobaczą, z jakich figur składa się ta bryła. To pomoże im zrozumieć, jak obliczyć pole powierzchni całkowitej i objętość.

4. Zadawaj pytania naprowadzające: Zamiast podawać gotowe definicje, zadawaj uczniom pytania, które skłonią ich do samodzielnego formułowania wniosków. Na przykład: "Jakie figury tworzą ściany boczne?", "Co wiesz o rombie?", "Jaki kąt tworzą ściany boczne z podstawą?".

5. Wykorzystaj przedmioty z życia codziennego: Poszukaj przedmiotów, które przypominają graniastosłup prosty o podstawie rombu (np. pewne rodzaje opakowań, elementy architektoniczne). Dzięki temu uczniowie zobaczą, że geometria jest obecna w otaczającym ich świecie.

Wzory i Obliczenia

Kluczowe wzory, które uczniowie powinni znać:

Pole powierzchni rombu (podstawy): P = a * h (gdzie 'a' to długość boku, 'h' to wysokość rombu) lub P = (d1 * d2) / 2 (gdzie d1 i d2 to długości przekątnych)
Pole powierzchni bocznej: Pb = 4 * a * H (gdzie 'a' to długość boku rombu, 'H' to wysokość graniastosłupa)
Pole powierzchni całkowitej: Pc = 2 * P + Pb (gdzie P to pole rombu, Pb to pole powierzchni bocznej)
Objętość: V = P * H (gdzie P to pole rombu, H to wysokość graniastosłupa)

Wskazówki dotyczące obliczeń:

Zwróć uwagę na jednostki: Upewnij się, że wszystkie wymiary są wyrażone w tej samej jednostce.
Podkreśl znaczenie rysunku pomocniczego: Zachęć uczniów do rysowania schematycznych rysunków, aby lepiej zrozumieć zadanie i zidentyfikować potrzebne dane.
Rozwiązuj zadania krok po kroku: Pokaż uczniom, jak rozkładać zadanie na mniejsze etapy. Najpierw oblicz pole podstawy, potem pole powierzchni bocznej, a na końcu pole powierzchni całkowitej i objętość.

Typowe Błędy i Jak Ich Unikać

1. Mylenie rombu z kwadratem: Jak już wspomniano, uczniowie często zakładają, że romb ma kąty proste. Przypominaj im, że jedynym rombem, który jest jednocześnie kwadratem, jest ten, który ma kąty proste.

2. Błędy w obliczaniu pola rombu: Uczniowie mogą zapominać o podzieleniu iloczynu przekątnych przez 2 lub mylić wysokość rombu z wysokością graniastosłupa.

3. Problem z orientacją w przestrzeni: Niektórzy uczniowie mają trudności z wyobrażeniem sobie bryły w przestrzeni i zidentyfikowaniem jej poszczególnych elementów. Pomagają w tym modele i wizualizacje 3D.

4. Zapominanie o wzorach: Regularne powtarzanie wzorów i rozwiązywanie zadań utrwala wiedzę. Można wykorzystać karty pracy, quizy online lub gry edukacyjne.

"Kluczem do sukcesu jest cierpliwość i systematyczna praca. Nie oczekuj, że uczniowie od razu wszystko zrozumieją. Daj im czas na przyswojenie wiedzy i zadawaj pytania, które sprawdzą ich zrozumienie."

Angażujące Metody Nauczania

1. Praca w grupach: Podziel uczniów na grupy i poproś ich o zbudowanie modelu graniastosłupa prostego o podstawie rombu z dostępnych materiałów (np. papier, karton, patyczki do szaszłyków). Następnie każda grupa prezentuje swój model i omawia jego własności.

2. Gry edukacyjne: Wykorzystaj gry planszowe, karciane lub online, które sprawdzają wiedzę uczniów na temat graniastosłupów. Można również zorganizować konkurs z nagrodami.

3. Projekty: Zaproponuj uczniom realizację projektu, w którym będą musieli zaprojektować i zbudować model budynku lub innego obiektu, który ma kształt graniastosłupa prostego o podstawie rombu. W ten sposób połączą teorię z praktyką.

4. Wykorzystanie technologii: Aplikacje do geometrii interaktywnej pozwalają na obracanie brył, analizowanie ich przekrojów i eksperymentowanie z różnymi parametrami. To bardzo angażujący sposób na naukę.

Przykładowe Zadania Aktywizujące

Zadanie praktyczne: "Zaprojektuj opakowanie na czekoladki w kształcie graniastosłupa prostego o podstawie rombu. Oblicz, ile papieru będziesz potrzebować na jego wykonanie, jeśli wiesz, że romb ma bok długości 5 cm i wysokość 4 cm, a wysokość graniastosłupa wynosi 10 cm."
Zadanie problemowe: "Masz do dyspozycji pręt o długości 1 metra. Chcesz z niego zbudować szkielet graniastosłupa prostego o podstawie rombu. Jakie powinny być wymiary rombu i wysokość graniastosłupa, aby objętość bryły była jak największa?"
Zadanie z wykorzystaniem technologii: "Użyj aplikacji do geometrii interaktywnej, aby zbadać, jak zmiana kąta ostrego w rombie wpływa na pole powierzchni bocznej graniastosłupa."

Pamiętajmy, że nauczanie geometrii przestrzennej wymaga od nauczyciela kreatywności i umiejętności angażowania uczniów. Wykorzystując różnorodne metody i narzędzia, możemy uczynić ten temat fascynującym i przystępnym dla każdego ucznia. Powodzenia!