Graniastosłup Prosty Ma W Podstawie Romb Krawędź Podstawy Ma 3m

Dobrze, przygotuję artykuł, który wyjaśni zagadnienie graniastosłupa prostego o podstawie w kształcie rombu, gdzie krawędź podstawy ma 3 metry. Postaram się, aby był on napisany prostym językiem, bez zbędnych definicji i zawierał minimalną liczbę matematycznych oznaczeń.

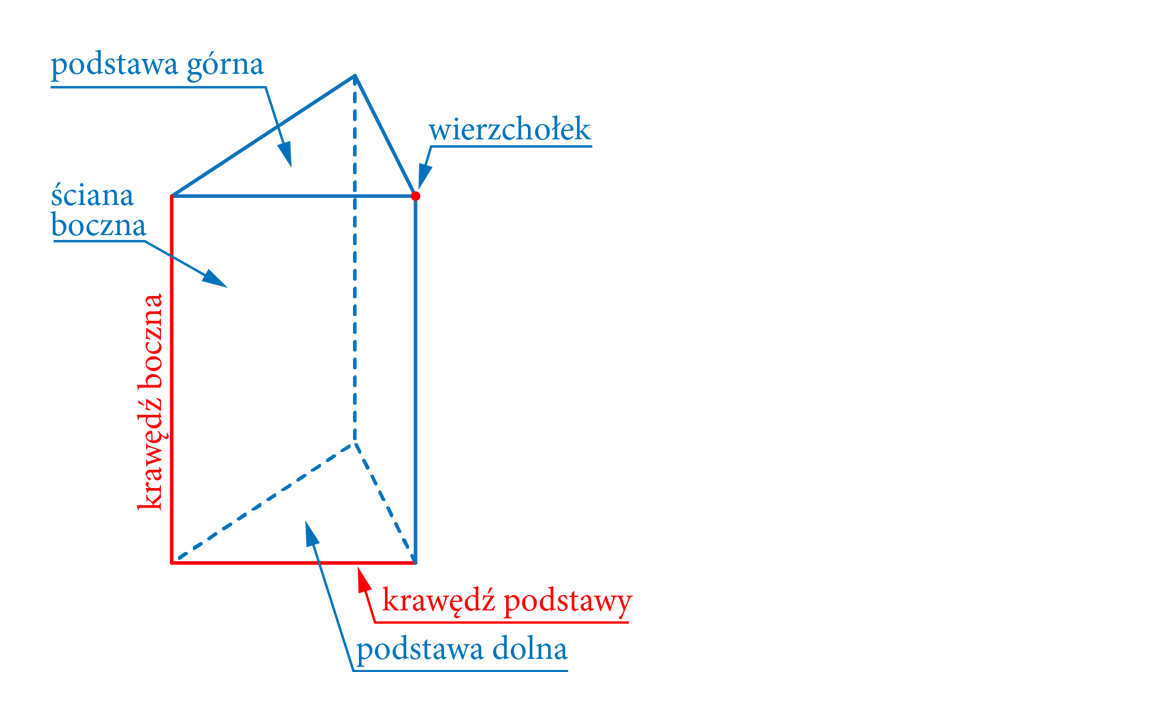
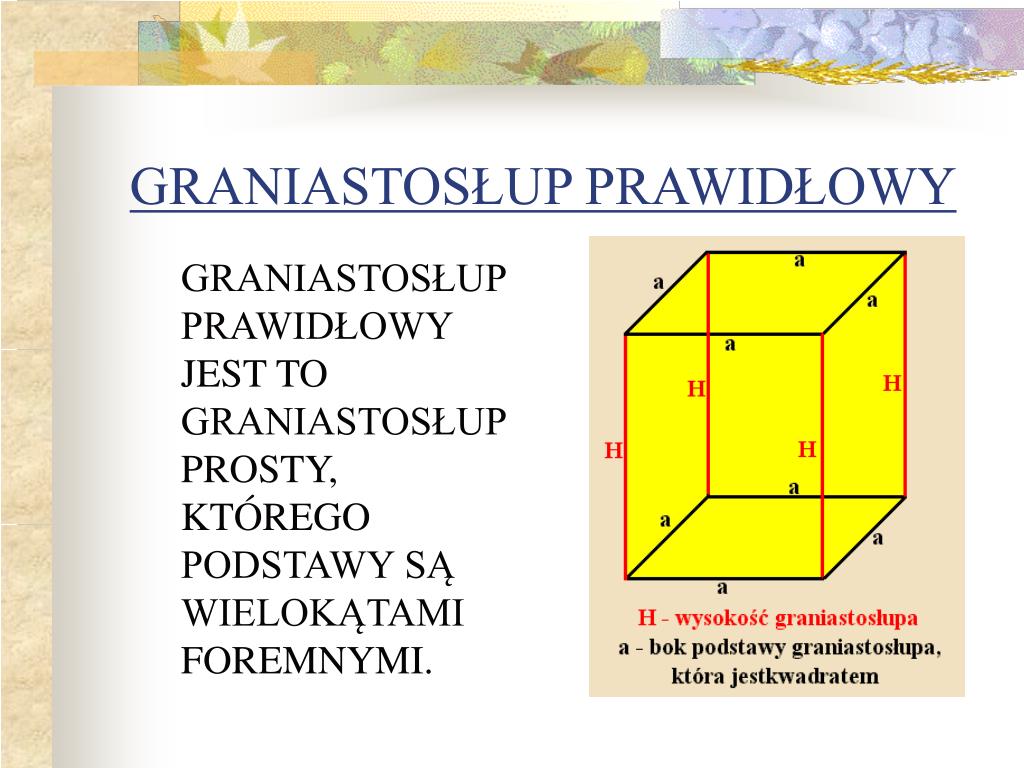
Mamy graniastosłup prosty. Wyobraź sobie pudełko, które stoi idealnie prosto na stole. To jest właśnie graniastosłup prosty. "Prosty" oznacza, że ściany boczne są prostopadłe do podstawy. Czyli kąt między ścianą boczną a podstawą wynosi 90 stopni.

Co to znaczy, że w podstawie jest romb? Romb to taka figura jak kwadrat, ale może być "ściśnięty" z jednej strony. Ma wszystkie boki równe, ale kąty niekoniecznie muszą być proste. W naszym przypadku podstawa, czyli to "dno" pudełka, ma właśnie kształt rombu.

Wiemy też, że krawędź podstawy ma 3 metry. Krawędź to po prostu bok rombu. Czyli każdy bok rombu, który jest podstawą naszego graniastosłupa, ma długość 3 metry. To bardzo ważna informacja!

Co możemy obliczyć?

Zastanówmy się, co możemy policzyć, mając takie informacje. Potrzebujemy więcej danych, żeby obliczyć konkretne wartości, ale możemy się zastanowić, czego możemy szukać.

1. Obwód podstawy: To bardzo proste! Romb ma 4 boki równej długości. Skoro każdy bok ma 3 metry, to obwód rombu (i zarazem obwód podstawy graniastosłupa) wynosi: 3m + 3m + 3m + 3m = 12 metrów. Obwód to po prostu suma długości wszystkich boków.

2. Pole podstawy: Żeby obliczyć pole rombu, potrzebujemy więcej informacji. Możemy to zrobić na kilka sposobów:

   • Jeśli znamy wysokość rombu: Wyobraź sobie, że romb stoi na jednym z boków. Wysokość to odległość od tego boku do przeciwległego wierzchołka (mierzona prostopadle). Pole rombu liczymy wtedy bardzo prosto: Pole = długość boku * wysokość. Skoro bok ma 3 metry, to Pole = 3m * wysokość. Jeśli na przykład wysokość rombu wynosi 2 metry, to Pole = 3m * 2m = 6 metrów kwadratowych.
   • Jeśli znamy długość przekątnych rombu: Romb ma dwie przekątne – krótszą i dłuższą. Przekątne przecinają się w połowie i pod kątem prostym. Pole rombu liczymy wtedy tak: Pole = (długość pierwszej przekątnej * długość drugiej przekątnej) / 2. Na przykład, jeśli jedna przekątna ma 4 metry, a druga 5 metrów, to Pole = (4m * 5m) / 2 = 10 metrów kwadratowych.
   • Jeśli znamy kąt ostry rombu: Romb ma dwa kąty ostre (mniejsze niż 90 stopni) i dwa kąty rozwarte (większe niż 90 stopni). Jeśli znamy miarę kąta ostrego, oznaczmy go jako α, to pole rombu można obliczyć ze wzoru: Pole = (bok * bok) * sin(α) = bok² * sin(α). Skoro bok ma 3 metry, to Pole = (3m)² * sin(α) = 9m² * sin(α). Trzeba pamiętać, że sinus kąta można odczytać z tablic matematycznych lub obliczyć za pomocą kalkulatora.

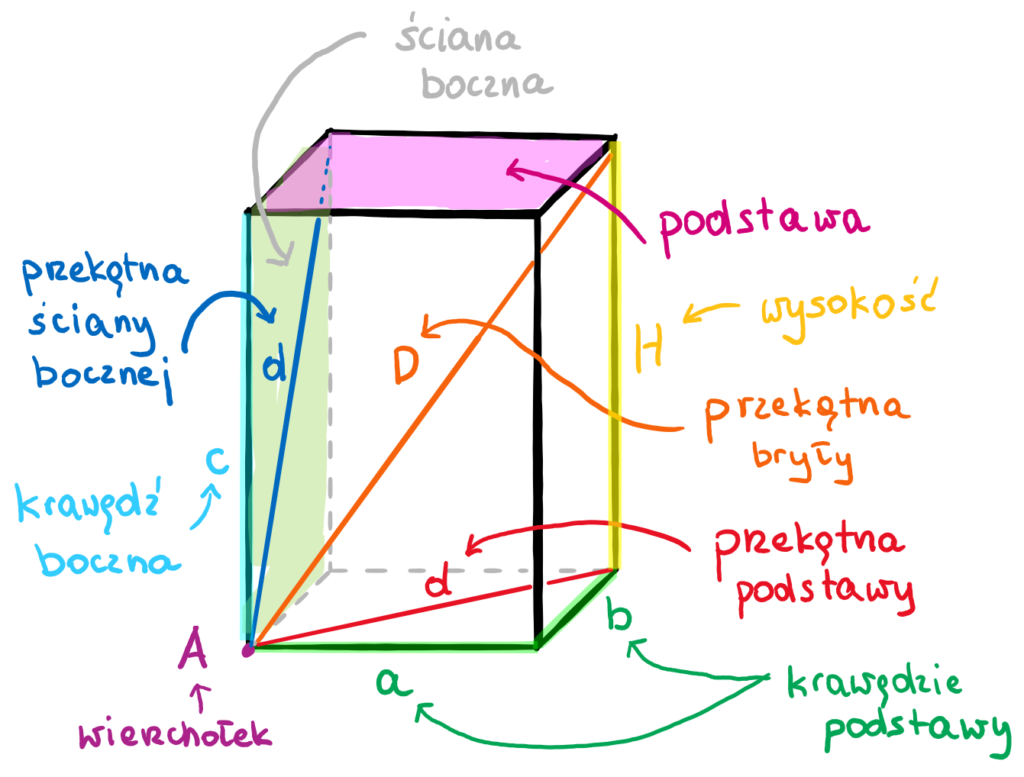
3. Pole powierzchni bocznej: Pole powierzchni bocznej to suma pól wszystkich ścian bocznych graniastosłupa. Skoro to graniastosłup prosty, to ściany boczne są prostokątami. Każdy prostokąt ma jeden bok równy krawędzi podstawy (czyli 3 metry), a drugi bok równy wysokości graniastosłupa. Oznaczmy wysokość graniastosłupa jako "H". Wtedy pole jednej ściany bocznej to 3m * H. Graniastosłup ma 4 ściany boczne (bo podstawa ma 4 boki), więc pole powierzchni bocznej wynosi: 4 * (3m * H) = 12m * H. Widzimy, że żeby obliczyć pole powierzchni bocznej, musimy znać wysokość graniastosłupa.

4. Pole powierzchni całkowitej: Pole powierzchni całkowitej to suma pól wszystkich ścian graniastosłupa – czyli pola dwóch podstaw (górnej i dolnej) oraz pola powierzchni bocznej. Pole jednej podstawy już omówiliśmy, więc pole dwóch podstaw to 2 * (pole rombu). Pole powierzchni bocznej też już omówiliśmy. Zatem Pole powierzchni całkowitej = 2 * (pole rombu) + (pole powierzchni bocznej). Czyli Pole powierzchni całkowitej = 2 * (pole rombu) + 12m * H. Znów widzimy, że potrzebujemy znać wysokość graniastosłupa i sposób obliczenia pola rombu (czyli wysokość rombu, długości przekątnych lub kąt ostry).

5. Objętość graniastosłupa: Objętość to ilość miejsca, jaką zajmuje graniastosłup. Objętość liczymy bardzo prosto: Objętość = (pole podstawy) * (wysokość graniastosłupa). Czyli Objętość = (pole rombu) * H. Podobnie jak w przypadku pola powierzchni całkowitej, musimy znać wysokość graniastosłupa i sposób obliczenia pola rombu.

Podsumowanie i przykłady

Widzimy, że mając tylko informację o długości krawędzi podstawy (3 metry), możemy obliczyć obwód podstawy. Natomiast żeby obliczyć pole podstawy, pole powierzchni bocznej, pole powierzchni całkowitej i objętość, potrzebujemy dodatkowych informacji, takich jak:

• Wysokość rombu
• Długości przekątnych rombu
• Kąt ostry rombu
• Wysokość graniastosłupa

Przykłady:

1. Załóżmy, że wysokość rombu wynosi 2 metry, a wysokość graniastosłupa wynosi 5 metrów. Wtedy:

   • Pole podstawy (rombu) = 3m * 2m = 6 metrów kwadratowych
   • Pole powierzchni bocznej = 12m * 5m = 60 metrów kwadratowych
   • Pole powierzchni całkowitej = 2 * (6m²) + 60m² = 12m² + 60m² = 72 metry kwadratowe
   • Objętość = 6m² * 5m = 30 metrów sześciennych

2. Załóżmy, że przekątne rombu mają długość 4 metry i 5 metrów, a wysokość graniastosłupa wynosi 10 metrów. Wtedy:

   • Pole podstawy (rombu) = (4m * 5m) / 2 = 10 metrów kwadratowych
   • Pole powierzchni bocznej = 12m * 10m = 120 metrów kwadratowych
   • Pole powierzchni całkowitej = 2 * (10m²) + 120m² = 20m² + 120m² = 140 metrów kwadratowych
   • Objętość = 10m² * 10m = 100 metrów sześciennych

Mam nadzieję, że teraz jest to bardziej zrozumiałe! Pamiętaj, że matematyka staje się łatwiejsza, gdy rozbijemy problem na mniejsze, zrozumiałe kroki.