Gdy Zaokrąglimy Liczbę 268 752 Do Dziesiątek Otrzymamy

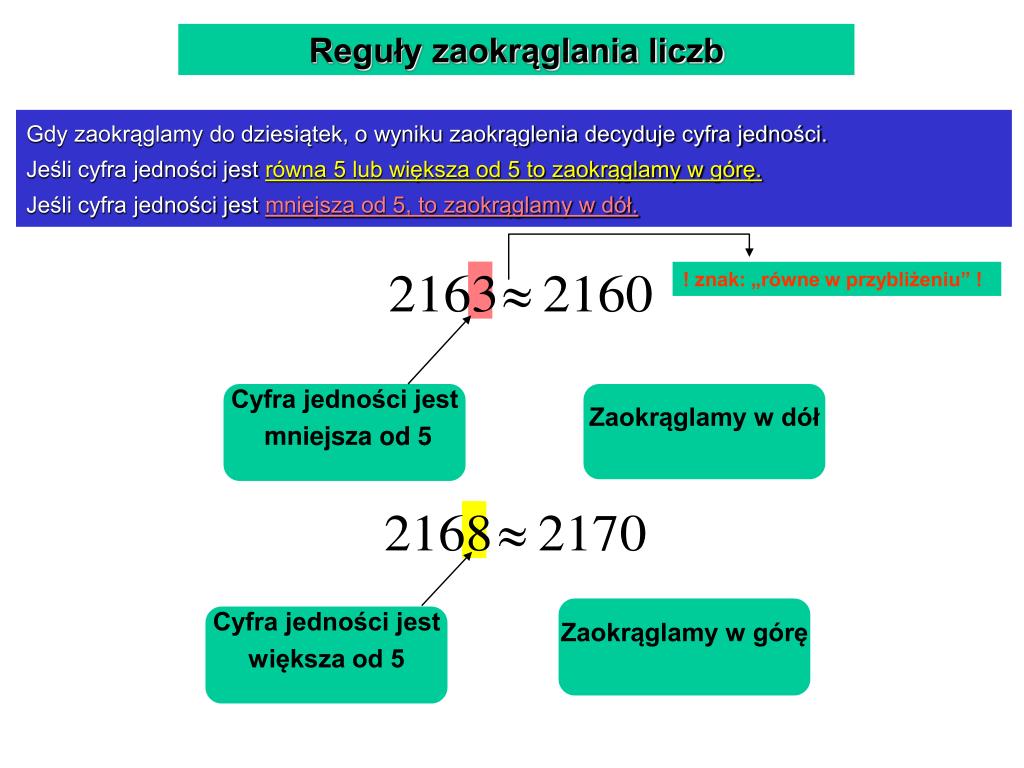
Gdy zaokrąglamy liczby, staramy się uprościć je, zachowując jednocześnie zbliżoną wartość. Robimy to, by łatwiej operować liczbami w przybliżonych obliczeniach lub przedstawiać je w bardziej czytelny sposób. Zaokrąglanie do dziesiątek oznacza, że chcemy, aby nasza liczba kończyła się na 0.

Żeby zaokrąglić liczbę 268 752 do dziesiątek, musimy spojrzeć na cyfrę jedności, czyli na ostatnią cyfrę w liczbie. W tym przypadku jest to cyfra 2.

Krok po kroku zaokrąglanie

1. Spójrz na cyfrę jedności: W naszej liczbie 268 752, cyfrą jedności jest 2.

2. Zdecyduj, w którą stronę zaokrąglić:

   • Jeśli cyfra jedności jest mniejsza niż 5 (0, 1, 2, 3, 4), zaokrąglamy w dół, czyli do najbliższej mniejszej dziesiątki.
   • Jeśli cyfra jedności jest 5 lub większa (5, 6, 7, 8, 9), zaokrąglamy w górę, czyli do najbliższej większej dziesiątki.

3. Zaokrąglenie: Ponieważ cyfra jedności w liczbie 268 752 to 2, czyli jest mniejsza niż 5, zaokrąglamy w dół. Oznacza to, że cyfra dziesiątek pozostaje bez zmian (w tym przypadku 5), a cyfrę jedności zamieniamy na 0.

Zatem, zaokrąglając liczbę 268 752 do dziesiątek, otrzymujemy 268 750.

Przykłady zaokrąglania do dziesiątek

• Zaokrąglając 17 do dziesiątek, patrzymy na cyfrę jedności, czyli 7. Ponieważ 7 jest większe niż 5, zaokrąglamy w górę do 20.
• Zaokrąglając 43 do dziesiątek, patrzymy na cyfrę jedności, czyli 3. Ponieważ 3 jest mniejsze niż 5, zaokrąglamy w dół do 40.
• Zaokrąglając 125 do dziesiątek, patrzymy na cyfrę jedności, czyli 5. Ponieważ 5 jest równe 5, zaokrąglamy w górę do 130.
• Zaokrąglając 987 do dziesiątek, patrzymy na cyfrę jedności, czyli 7. Ponieważ 7 jest większe niż 5, zaokrąglamy w górę do 990.
• Zaokrąglając 342 do dziesiątek, patrzymy na cyfrę jedności, czyli 2. Ponieważ 2 jest mniejsze niż 5, zaokrąglamy w dół do 340.

Dlaczego to jest użyteczne?

Zaokrąglanie jest przydatne w wielu sytuacjach. Wyobraź sobie, że mówisz komuś o cenie samochodu. Zamiast powiedzieć, że kosztuje on 34 876 zł, możesz powiedzieć, że kosztuje około 34 880 zł lub nawet 34 900 zł. To sprawia, że liczba jest łatwiejsza do zapamiętania i zrozumienia.

Innym przykładem jest szacowanie kosztów zakupów. Jeśli w sklepie kupujesz produkty za 12,45 zł, 8,99 zł i 5,20 zł, możesz szybko zaokrąglić te kwoty do 12 zł, 9 zł i 5 zł i oszacować, że zapłacisz około 26 zł. To znacznie szybciej niż dokładne sumowanie tych kwot w głowie.

Zaokrąglanie jest również ważne w nauce, np. w fizyce i chemii, gdzie często operujemy liczbami z niepewnością pomiarową. Zaokrąglanie pozwala na uproszczenie wyników i uniknięcie wrażenia fałszywej precyzji.

Podsumowanie

Zaokrąglanie do dziesiątek polega na uproszczeniu liczby tak, aby kończyła się na 0. Decyzja o zaokrągleniu w górę lub w dół zależy od cyfry jedności. Jeśli cyfra jedności jest mniejsza niż 5, zaokrąglamy w dół, a jeśli jest równa 5 lub większa, zaokrąglamy w górę. W przypadku liczby 268 752, zaokrąglając ją do dziesiątek, otrzymujemy 268 750. Zaokrąglanie jest bardzo przydatne w życiu codziennym, ułatwiając szacowanie, upraszczanie liczb i przedstawianie ich w bardziej czytelny sposób. Jest to podstawowa umiejętność matematyczna, która znajduje zastosowanie w wielu różnych sytuacjach. Pamiętaj o prostych zasadach i ćwicz regularnie, aby zaokrąglanie stało się dla Ciebie naturalne i intuicyjne. Zaokrąglanie, choć wydaje się proste, jest niezwykle ważne w kontekście analizy danych i prezentacji wyników. Pomaga uniknąć wprowadzania odbiorców w błąd poprzez nadmierną precyzję, która często nie jest uzasadniona dokładnością pomiarów czy obliczeń.

Zaokrąglanie, tak jak wspomniano, ma wiele zastosowań w życiu codziennym. Spróbuj zastosować je w różnych sytuacjach, np. planując budżet domowy, szacując czas potrzebny na wykonanie jakiegoś zadania, czy porównując ceny produktów w sklepie. Im częściej będziesz korzystać z zaokrąglania, tym łatwiej i szybciej będziesz to robić.

Warto również pamiętać, że zaokrąglanie może prowadzić do pewnych błędów. Im większe zaokrąglenie, tym większy potencjalny błąd. Dlatego ważne jest, aby zastanowić się, do jakiej dokładności chcemy zaokrąglić liczbę, biorąc pod uwagę kontekst i cel, jaki chcemy osiągnąć. W niektórych sytuacjach dokładne obliczenia są niezbędne, a zaokrąglanie może prowadzić do nieakceptowalnych błędów.

Mimo potencjalnych błędów, zaokrąglanie pozostaje niezwykle użytecznym narzędziem, które pozwala na uproszczenie i zrozumienie liczb. Naucz się z niego korzystać mądrze i świadomie, a z pewnością ułatwi Ci to wiele codziennych czynności.

Zatem, pamiętaj, że gdy zaokrąglimy liczbę 268 752 do dziesiątek, otrzymamy 268 750.