Funkcje Trygonometryczne Kąta Ostrego W Trójkącie Prostokątnym

W trójkącie prostokątnym, gdzie jeden z kątów ma miarę 90 stopni, dwa pozostałe kąty są ostre, czyli mniejsze niż 90 stopni. Funkcje trygonometryczne kąta ostrego pozwalają nam powiązać miary kątów z długościami boków tego trójkąta. Skupimy się na trzech podstawowych funkcjach: sinusie (sin), cosinusie (cos) i tangensie (tg), a także na ich odwrotnościach: cotangensie (ctg), secansie (sec) i cosecansie (cosec).

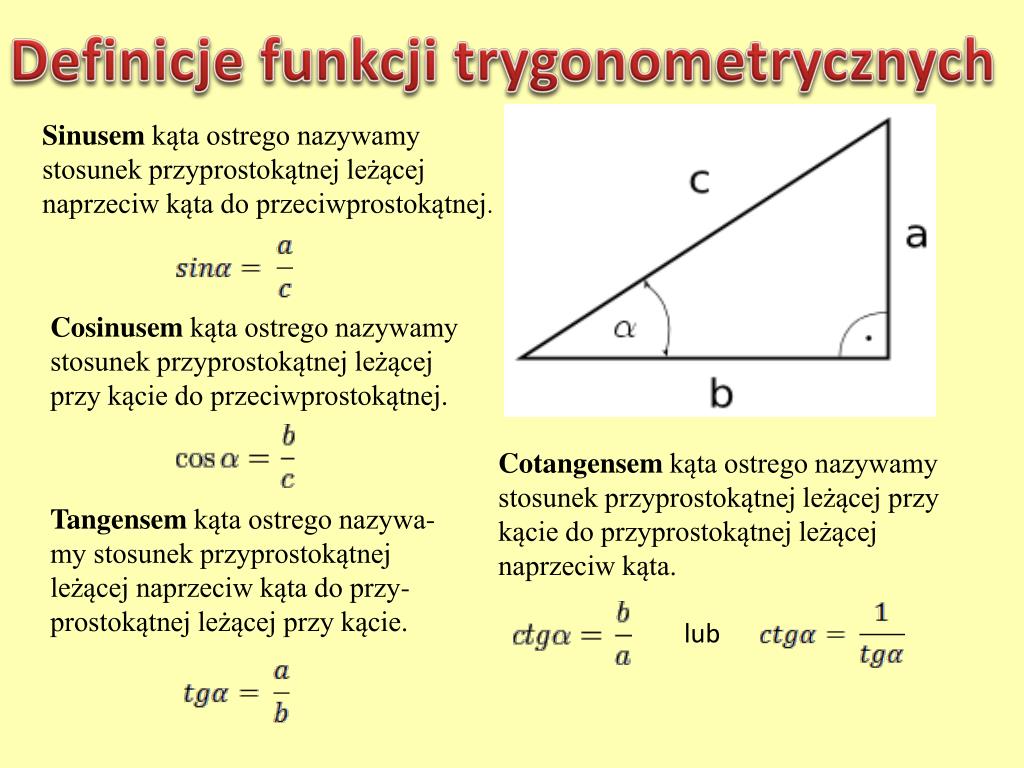
Rozważmy trójkąt prostokątny ABC, gdzie kąt przy wierzchołku C jest prosty. Bok leżący naprzeciw kąta prostego, bok AB, nazywamy przeciwprostokątną. Pozostałe dwa boki, AC i BC, nazywamy przyprostokątnymi. Wybierzmy jeden z kątów ostrych, na przykład kąt przy wierzchołku A. Względem tego kąta możemy zdefiniować przyprostokątną przyległą (czyli bok AC, który tworzy ramię kąta A) i przyprostokątną przeciwległą (czyli bok BC, leżący naprzeciw kąta A).

Definicje funkcji trygonometrycznych dla kąta ostrego A w trójkącie prostokątnym ABC, gdzie kąt C jest prosty, wyglądają następująco:

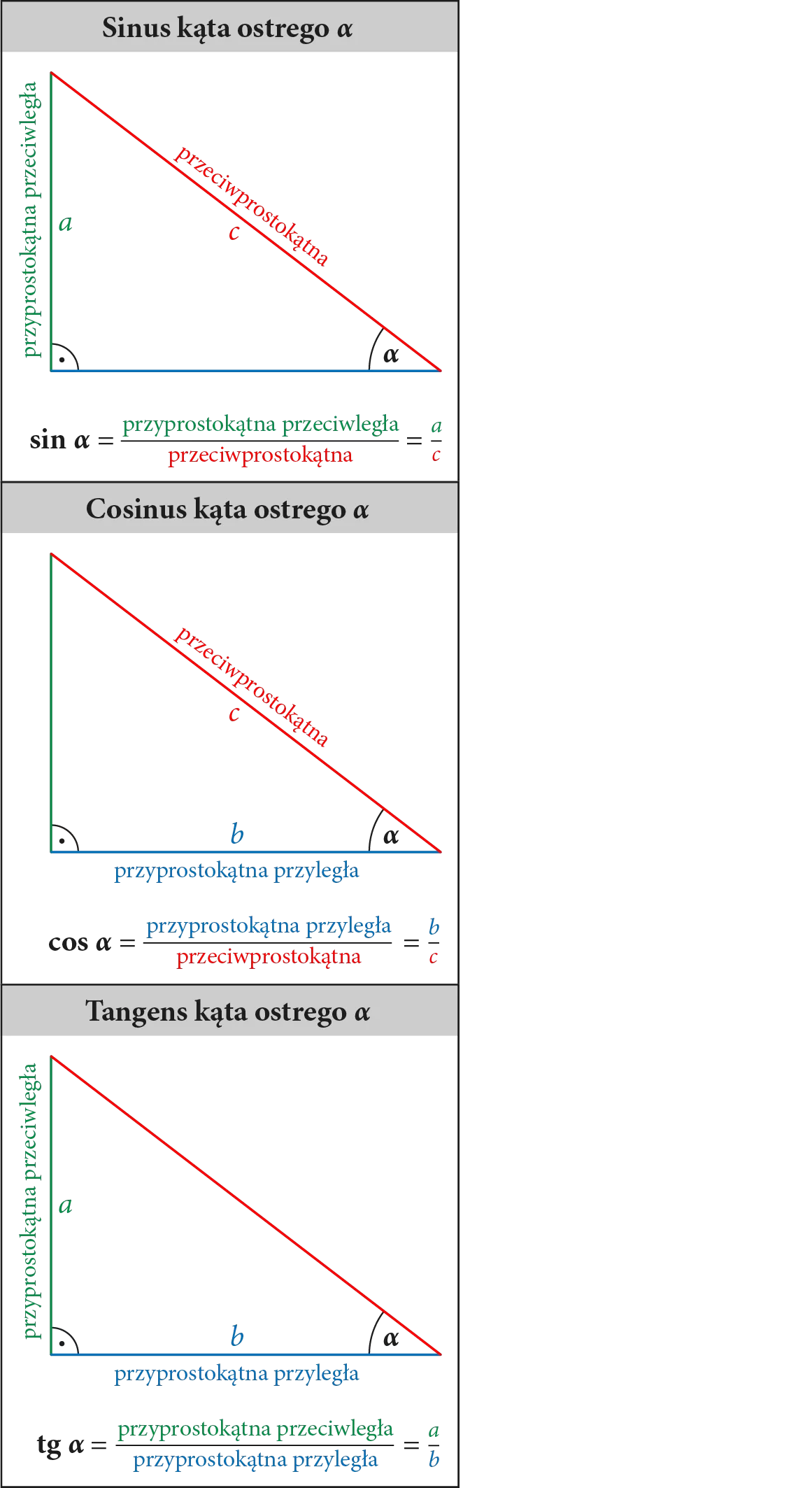
sinus kąta A (sin A) to stosunek długości przyprostokątnej przeciwległej do długości przeciwprostokątnej: sin A = BC / AB
cosinus kąta A (cos A) to stosunek długości przyprostokątnej przyległej do długości przeciwprostokątnej: cos A = AC / AB
tangens kąta A (tg A) to stosunek długości przyprostokątnej przeciwległej do długości przyprostokątnej przyległej: tg A = BC / AC

Funkcje odwrotne definiujemy następująco:

cotangens kąta A (ctg A) to stosunek długości przyprostokątnej przyległej do długości przyprostokątnej przeciwległej: ctg A = AC / BC. Zauważmy, że ctg A = 1 / tg A.
secans kąta A (sec A) to stosunek długości przeciwprostokątnej do długości przyprostokątnej przyległej: sec A = AB / AC. Zauważmy, że sec A = 1 / cos A.
cosecans kąta A (cosec A) to stosunek długości przeciwprostokątnej do długości przyprostokątnej przeciwległej: cosec A = AB / BC. Zauważmy, że cosec A = 1 / sin A.

Wyobraźmy sobie trójkąt prostokątny, w którym przyprostokątna przyległa do kąta ostrego A ma długość 3, przyprostokątna przeciwległa ma długość 4, a przeciwprostokątna ma długość 5. Wtedy:

sin A = 4 / 5 = 0.8
cos A = 3 / 5 = 0.6
tg A = 4 / 3 ≈ 1.33
ctg A = 3 / 4 = 0.75
sec A = 5 / 3 ≈ 1.67
cosec A = 5 / 4 = 1.25

Zależności między funkcjami trygonometrycznymi

Funkcje trygonometryczne powiązane są ze sobą szeregiem zależności. Najważniejszą z nich jest tzw. jedynka trygonometryczna:

sin²A + cos²A = 1

Wynika ona bezpośrednio z twierdzenia Pitagorasa. Podzielmy obie strony równania a² + b² = c² (gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej) przez c². Otrzymujemy (a/c)² + (b/c)² = 1. Zauważamy, że a/c to cosinus kąta ostrego przyległego do boku 'a', a b/c to sinus tego kąta. Stąd otrzymujemy sin²A + cos²A = 1.

Inne ważne zależności wynikają z definicji funkcji odwrotnych oraz z samej definicji tangensa:

tg A = sin A / cos A ctg A = cos A / sin A

Dzięki tym zależnościom, znając wartość jednej funkcji trygonometrycznej kąta ostrego, możemy obliczyć wartości pozostałych funkcji.

Kąty Charakterystyczne

Dla pewnych kątów ostrych, takich jak 30°, 45° i 60°, wartości funkcji trygonometrycznych można wyrazić za pomocą liczb niewymiernych. Warto je zapamiętać, ponieważ często pojawiają się w zadaniach.

Dla kąta 30°:

sin 30° = 1/2
cos 30° = √3 / 2
tg 30° = √3 / 3
ctg 30° = √3

Dla kąta 45°:

sin 45° = √2 / 2
cos 45° = √2 / 2
tg 45° = 1
ctg 45° = 1

Dla kąta 60°:

sin 60° = √3 / 2
cos 60° = 1/2
tg 60° = √3
ctg 60° = √3 / 3

Zauważmy, że sinus kąta 30° jest równy cosinusowi kąta 60°, sinus kąta 60° jest równy cosinusowi kąta 30°, a tangens kąta 30° jest odwrotnością tangensa kąta 60°. Jest to związane z faktem, że kąty 30° i 60° są kątami dopełniającymi się do 90° (czyli 30° + 60° = 90°). W ogólności, dla dowolnych kątów α i β, takich że α + β = 90°, zachodzą następujące równości:

sin α = cos β cos α = sin β tg α = ctg β ctg α = tg β

Zastosowania Funkcji Trygonometrycznych

Funkcje trygonometryczne kąta ostrego znajdują szerokie zastosowanie w różnych dziedzinach, takich jak:

Geometria: Obliczanie długości boków i miar kątów w trójkątach prostokątnych i skośnokątnych.
Fizyka: Opis ruchu harmonicznego, fal, rzutów ukośnych.
Nawigacja: Określanie kierunków i odległości.
Inżynieria: Projektowanie budynków, mostów, maszyn.
Astronomia: Obliczanie odległości do gwiazd i planet.

Na przykład, za pomocą funkcji trygonometrycznych można obliczyć wysokość drzewa, mierząc kąt pod jakim widzimy jego wierzchołek z pewnej odległości od jego podstawy, oraz mierząc tę odległość. Podobnie, można obliczyć szerokość rzeki, mierząc kąty i odległości na jednym z jej brzegów.

Przykładowe Zadania

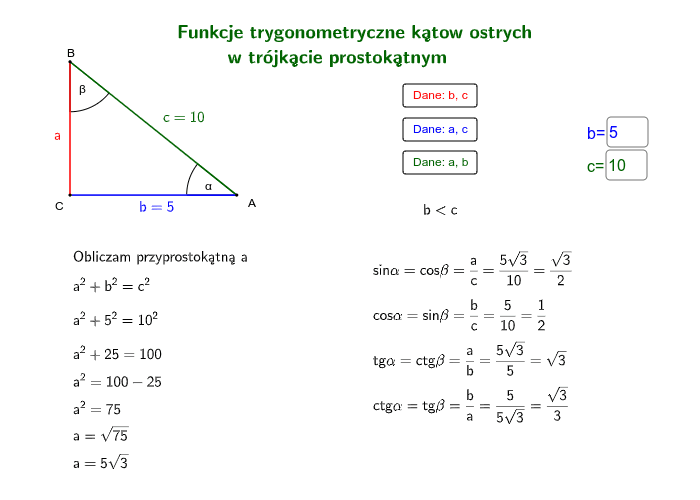
W trójkącie prostokątnym ABC, kąt C jest prosty, bok AC ma długość 6, a bok BC ma długość 8. Oblicz wartości funkcji trygonometrycznych kąta A.

Rozwiązanie: Najpierw obliczamy długość przeciwprostokątnej AB, korzystając z twierdzenia Pitagorasa: AB² = AC² + BC² = 6² + 8² = 36 + 64 = 100. Stąd AB = √100 = 10. Teraz możemy obliczyć wartości funkcji trygonometrycznych: sin A = BC / AB = 8 / 10 = 0.8 cos A = AC / AB = 6 / 10 = 0.6 tg A = BC / AC = 8 / 6 = 4/3 ctg A = AC / BC = 6 / 8 = 3/4 sec A = AB / AC = 10 / 6 = 5/3 cosec A = AB / BC = 10 / 8 = 5/4
Kąt nachylenia drabiny do ściany wynosi 60°. Drabina ma długość 4 metry. Na jakiej wysokości drabina opiera się o ścianę?

Rozwiązanie: Wysokość, na jakiej drabina opiera się o ścianę, to długość przyprostokątnej przeciwległej do kąta 60°. Zatem: sin 60° = wysokość / długość drabiny √3 / 2 = wysokość / 4 wysokość = 4 * (√3 / 2) = 2√3 metry.

Funkcje trygonometryczne kąta ostrego w trójkącie prostokątnym stanowią fundament wielu działów matematyki i fizyki. Zrozumienie ich definicji, zależności między nimi oraz umiejętność ich stosowania jest kluczowe do rozwiązywania problemów geometrycznych i fizycznych. Zachęcam do dalszej eksploracji tego fascynującego tematu poprzez rozwiązywanie zadań i analizę różnych przykładów zastosowań.