Funkcja Wykładnicza I Logarytmiczna Sprawdzian Nowa Era

Witajcie, drodzy uczniowie!

Widzę, że macie pytania dotyczące sprawdzianu z funkcji wykładniczej i logarytmicznej Nowej Ery. Postaram się wam to wszystko jak najprościej wytłumaczyć, tak żebyście bez problemu poradzili sobie z zadaniami. Skupimy się na najważniejszych elementach, które na pewno się pojawią.

Na sprawdzianie na pewno pojawią się zadania związane z rozpoznawaniem funkcji wykładniczych i logarytmicznych. Funkcja wykładnicza ma wzór ogólny f(x) = a^x, gdzie 'a' to podstawa potęgi i jest liczbą dodatnią różną od 1. Czyli, żeby coś było funkcją wykładniczą, 'x' musi być w wykładniku potęgi. Na przykład, 2^x, (1/3)^x, π^x – to wszystko są funkcje wykładnicze. Funkcja logarytmiczna to w pewnym sensie odwrotność funkcji wykładniczej. Ma wzór ogólny f(x) = log_a(x), gdzie 'a' to podstawa logarytmu (też dodatnia i różna od 1), a 'x' jest argumentem logarytmu (musi być liczbą dodatnią). Czyli log_2(x), log_0.5(x), log_10(x) – to funkcje logarytmiczne. Ważne, żeby rozróżniać te dwa typy funkcji, bo często w zadaniach trzeba po prostu stwierdzić, czy dany wzór to funkcja wykładnicza, logarytmiczna, czy żadna z nich.

Kolejna ważna sprawa to rysowanie wykresów funkcji wykładniczych i logarytmicznych. Spróbujmy narysować wykres funkcji f(x) = 2^x. Żeby to zrobić, najlepiej jest zrobić tabelkę z kilkoma wartościami 'x' i odpowiadającymi im wartościami 'f(x)'. Na przykład:

• x = -2, f(x) = 2^(-2) = 1/4
• x = -1, f(x) = 2^(-1) = 1/2
• x = 0, f(x) = 2^0 = 1
• x = 1, f(x) = 2^1 = 2
• x = 2, f(x) = 2^2 = 4

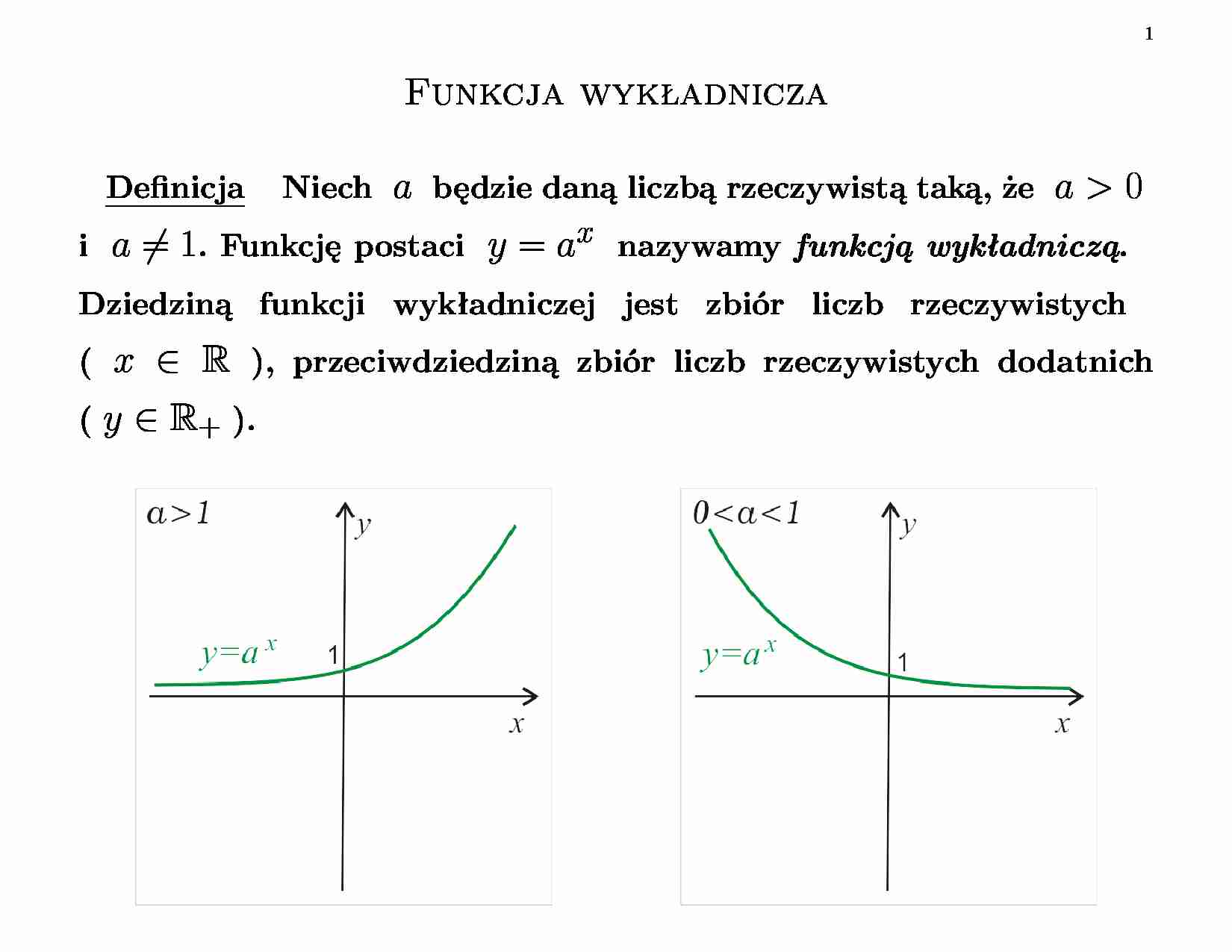
Teraz zaznaczamy te punkty na układzie współrzędnych i rysujemy gładką linię przechodzącą przez te punkty. Zauważ, że wykres funkcji wykładniczej nigdy nie dotyka osi OX. Zbliża się do niej coraz bardziej, ale nigdy jej nie przecina. Dodatkowo, dla a > 1 (w naszym przykładzie a = 2), funkcja jest rosnąca. Oznacza to, że im większe 'x', tym większe 'f(x)'. Jeśli a < 1 (na przykład f(x) = (1/2)^x), to funkcja jest malejąca.

Teraz narysujmy wykres funkcji logarytmicznej, na przykład f(x) = log_2(x). Robimy podobnie: tworzymy tabelkę. Pamiętaj, że argument logarytmu (czyli 'x' w naszym przypadku) musi być liczbą dodatnią.

• x = 1/4, f(x) = log_2(1/4) = -2
• x = 1/2, f(x) = log_2(1/2) = -1
• x = 1, f(x) = log_2(1) = 0
• x = 2, f(x) = log_2(2) = 1
• x = 4, f(x) = log_2(4) = 2

Zaznaczamy te punkty na układzie współrzędnych i rysujemy gładką linię. Wykres funkcji logarytmicznej nigdy nie dotyka osi OY. Zbliża się do niej coraz bardziej, ale nigdy jej nie przecina. Dla a > 1 (w naszym przykładzie a = 2), funkcja jest rosnąca. Jeśli a < 1, to funkcja jest malejąca. Zauważ, że wykres funkcji logarytmicznej log_a(x) jest symetryczny do wykresu funkcji wykładniczej a^x względem prostej y = x.

Przesuwanie Wykresów

Kolejna rzecz, która może się pojawić na sprawdzianie, to przesuwanie wykresów funkcji wykładniczych i logarytmicznych. Załóżmy, że mamy funkcję f(x) = 2^x i chcemy narysować wykres funkcji g(x) = 2^(x-1) + 3. Co się zmieniło? Mamy (x-1) w wykładniku i dodane +3 na końcu.

• (x-1) w wykładniku oznacza przesunięcie wykresu funkcji f(x) w prawo o 1 jednostkę.
• +3 na końcu oznacza przesunięcie wykresu funkcji f(x) w górę o 3 jednostki.

Czyli, żeby narysować wykres funkcji g(x), rysujemy najpierw wykres funkcji f(x) = 2^x, a potem przesuwamy go o 1 jednostkę w prawo i o 3 jednostki w górę. Analogicznie działa to dla funkcji logarytmicznych. Jeśli mamy funkcję h(x) = log_2(x+2) - 1, to przesuwamy wykres funkcji f(x) = log_2(x) o 2 jednostki w lewo (bo mamy x+2) i o 1 jednostkę w dół (bo mamy -1).

Bardzo ważne jest też rozwiązywanie równań wykładniczych i logarytmicznych. Przykład: rozwiąż równanie 2^x = 8. Możemy zapisać 8 jako 2^3. Czyli mamy 2^x = 2^3. Z tego wynika, że x = 3. To jest prosty przykład, ale idea jest taka: staramy się doprowadzić do tego, żeby po obu stronach równania mieć potęgi o tej samej podstawie. Wtedy możemy porównać wykładniki.

A co, jeśli mamy równanie 2^(x+1) = 16? Znów, 16 możemy zapisać jako 2^4. Czyli mamy 2^(x+1) = 2^4. Porównujemy wykładniki: x+1 = 4. Z tego wynika, że x = 3.

Równania logarytmiczne rozwiązuje się podobnie. Na przykład: rozwiąż równanie log_2(x) = 3. Z definicji logarytmu wiemy, że x = 2^3. Czyli x = 8. Ważne jest, żeby pamiętać o dziedzinie logarytmu. Argument logarytmu musi być liczbą dodatnią. Czyli, jeśli w równaniu logarytmicznym wychodzi nam rozwiązanie ujemne, to odrzucamy je. Na przykład, jeśli po rozwiązaniu równania log_2(x+3) = 1 wyszłoby nam x = -5, to odrzucamy to rozwiązanie, bo x+3 musiałoby być liczbą dodatnią.

Własności Logarytmów

Na sprawdzianie na pewno pojawią się zadania związane z własnościami logarytmów. Przypomnijmy sobie najważniejsze:

• log_a(1) = 0 (logarytm z jedynki o dowolnej podstawie jest równy zero)
• log_a(a) = 1 (logarytm z liczby 'a' o podstawie 'a' jest równy jeden)
• log_a(x*y) = log_a(x) + log_a(y) (logarytm z iloczynu to suma logarytmów)
• log_a(x/y) = log_a(x) - log_a(y) (logarytm z ilorazu to różnica logarytmów)
• log_a(x^n) = n * log_a(x) (wykładnik potęgi możemy "wyciągnąć" przed logarytm)

Te własności pozwalają nam upraszczać wyrażenia logarytmiczne i rozwiązywać bardziej skomplikowane równania. Na przykład, mamy wyrażenie log_2(4x) - log_2(2). Możemy to uprościć używając własności logarytmu z ilorazu: log_2(4x/2) = log_2(2x).

Inny przykład: log_3(9^2). Możemy to uprościć na dwa sposoby: albo obliczyć 9^2 = 81 i wtedy mamy log_3(81) = 4, albo użyć własności logarytmu z potęgi: 2 * log_3(9) = 2 * 2 = 4.

Pamiętajcie też o wzorze na zmianę podstawy logarytmu: log_a(b) = log_c(b) / log_c(a). Ten wzór przydaje się, gdy mamy logarytmy o różnych podstawach i chcemy je sprowadzić do tej samej podstawy.

Mam nadzieję, że to wszystko pomogło wam lepiej zrozumieć funkcje wykładnicze i logarytmiczne. Pamiętajcie o ćwiczeniu rozwiązywania zadań. Im więcej zadań zrobicie, tym lepiej będziecie przygotowani do sprawdzianu. Powodzenia!

I pamiętajcie, żeby przed sprawdzianem dobrze się wyspać i zjeść śniadanie. To też pomaga! :)