Funkcja Logarytmiczna I Wykładnicza Sprawdzian

Funkcja logarytmiczna i funkcja wykładnicza to dwa ważne pojęcia w matematyce. Są one ze sobą ściśle powiązane. Zrozumienie ich zasad jest kluczowe w rozwiązywaniu wielu problemów.

Funkcja Wykładnicza

Funkcja wykładnicza ma postać f(x) = a^x. a to podstawa, która musi być liczbą dodatnią różną od 1 (a > 0 i a ≠ 1). x to zmienna niezależna, która jest wykładnikiem. Wykres funkcji wykładniczej rośnie (gdy a > 1) lub maleje (gdy 0 < a < 1) wraz ze wzrostem x.

Przykład: f(x) = 2^x. Dla x = 0 mamy f(0) = 2⁰ = 1. Dla x = 1 mamy f(1) = 2¹ = 2. Dla x = 2 mamy f(2) = 2² = 4. Zauważ, że funkcja rośnie bardzo szybko.

Funkcje wykładnicze są używane do modelowania wzrostu populacji, rozpadu promieniotwórczego i oprocentowania składanego. Są szeroko stosowane w biologii, fizyce i finansach. Wiedza o ich właściwościach pomaga w analizie danych.

Funkcja Logarytmiczna

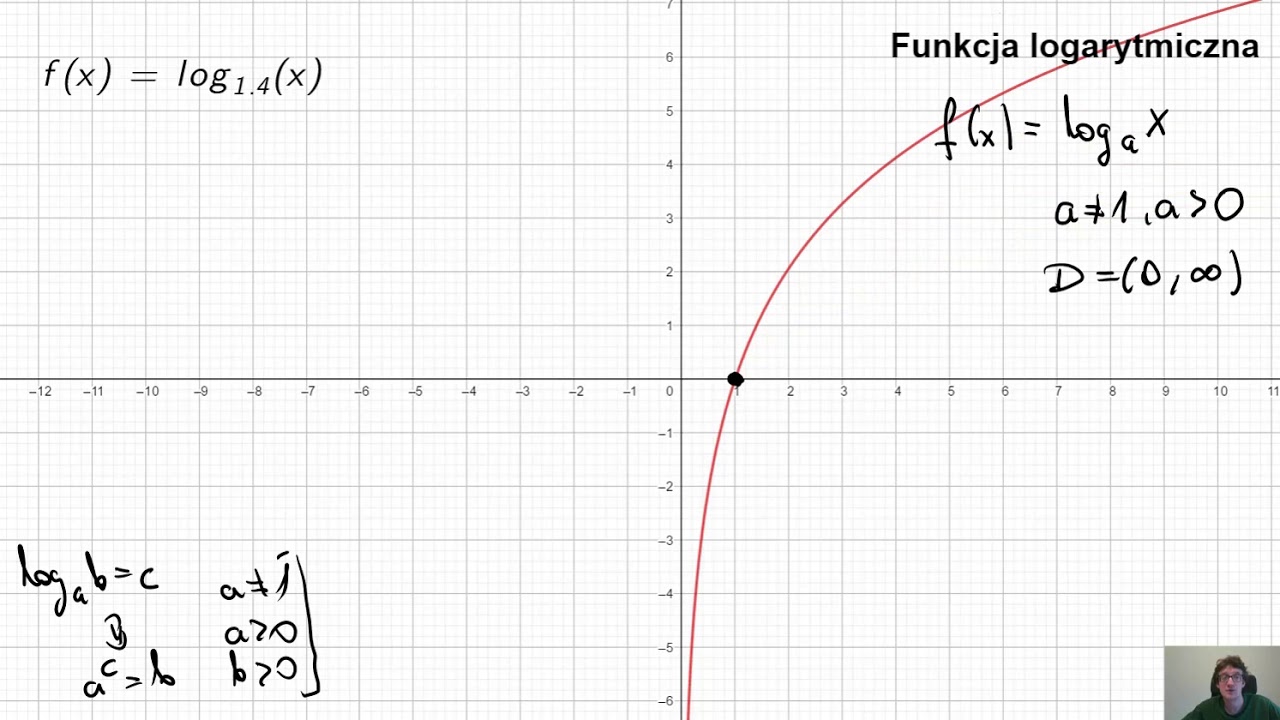
Funkcja logarytmiczna jest odwrotnością funkcji wykładniczej. Ma postać f(x) = log_a(x). a to podstawa logarytmu (a > 0 i a ≠ 1). x to argument logarytmu, który musi być liczbą dodatnią (x > 0). Funkcja logarytmiczna pokazuje, do jakiej potęgi trzeba podnieść podstawę a, aby otrzymać x.

Przykład: f(x) = log₂(x). log₂(8) = 3, ponieważ 2³ = 8. log₂(16) = 4, ponieważ 2⁴ = 16. Zauważ, że funkcja rośnie wolniej niż funkcja wykładnicza.

Funkcje logarytmiczne są używane do rozwiązywania równań wykładniczych. Są również stosowane w skalach logarytmicznych, takich jak skala Richtera do pomiaru trzęsień ziemi. Znajdują zastosowanie w chemii (pH) i akustyce (decybele). Ich właściwości ułatwiają pracę z bardzo dużymi lub bardzo małymi liczbami.

Sprawdzian

Sprawdzian z funkcji logarytmicznej i wykładniczej może obejmować zadania związane z obliczaniem wartości funkcji dla danego argumentu. Może również dotyczyć rozwiązywania równań i nierówności wykładniczych i logarytmicznych. Ważne jest zrozumienie definicji i właściwości tych funkcji.

Przykładowe zadanie: Rozwiąż równanie 2^x = 8. Rozwiązanie: x = log₂(8) = 3.

Pamiętaj, że funkcja wykładnicza i logarytmiczna są wzajemnie odwrotne. Zrozumienie tej zależności jest kluczem do sukcesu na sprawdzianie.