Funkcja Liniowa Zadania I Rozwiązania
Funkcja liniowa to jedno z fundamentalnych pojęć w matematyce, szczególnie istotne w algebrze i geometrii analitycznej. Rozumienie funkcji liniowych, ich własności oraz umiejętność rozwiązywania zadań z nimi związanych, jest kluczowe dla dalszego rozwoju w matematyce i jej zastosowaniach w innych dziedzinach. Ten artykuł skupi się na dogłębnym omówieniu funkcji liniowej, prezentując różnorodne zadania wraz z rozwiązaniami, aby pomóc w zrozumieniu tego zagadnienia.
Podstawy Funkcji Liniowej
Definicja i Wzór Ogólny
Funkcja liniowa to funkcja, którą można opisać wzorem:
f(x) = ax + b
Gdzie:
- x to zmienna niezależna (argument funkcji).
- f(x) lub y to zmienna zależna (wartość funkcji).
- a to współczynnik kierunkowy prostej. Określa nachylenie prostej względem osi OX.
- b to wyraz wolny. Określa punkt przecięcia prostej z osią OY.
Graficznie, funkcja liniowa przedstawiana jest jako prosta linia na układzie współrzędnych.
Współczynnik Kierunkowy (a)
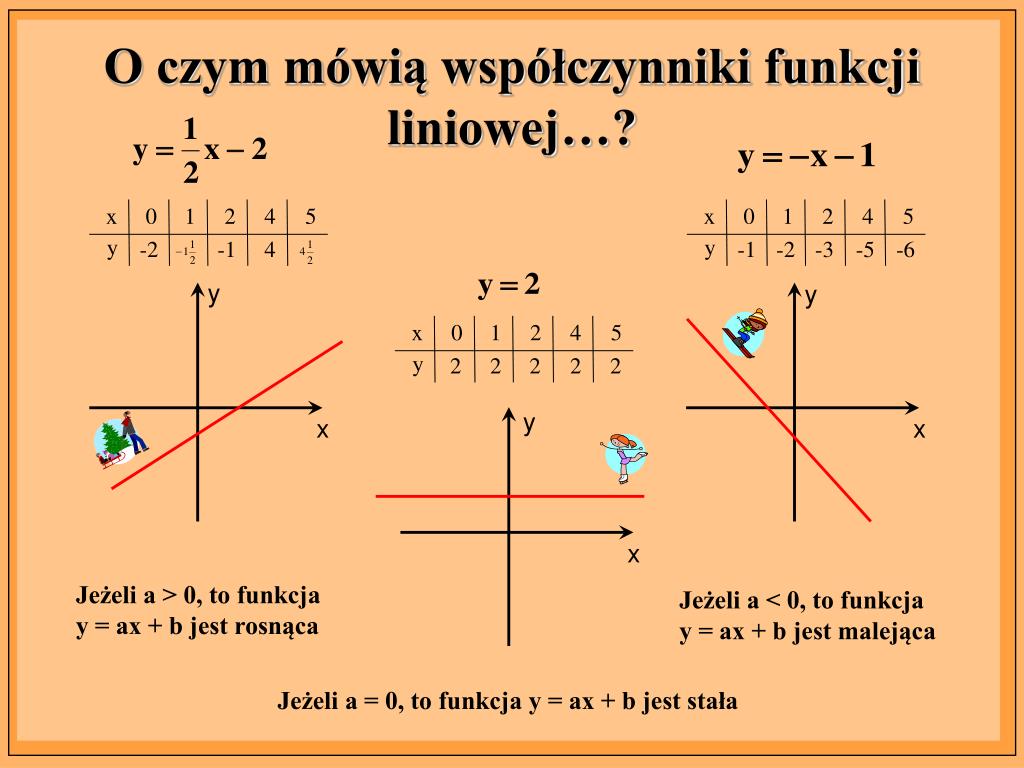
Współczynnik kierunkowy a ma kluczowe znaczenie. Określa, czy funkcja jest rosnąca, malejąca czy stała:
- a > 0: Funkcja jest rosnąca (im większe x, tym większe f(x)).
- a < 0: Funkcja jest malejąca (im większe x, tym mniejsze f(x)).
- a = 0: Funkcja jest stała (f(x) = b dla każdego x). Jej wykresem jest linia pozioma).
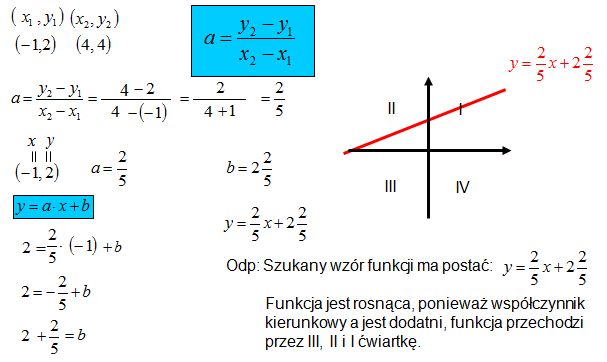
Możemy obliczyć współczynnik kierunkowy a, znając dwa punkty leżące na prostej, np. (x1, y1) i (x2, y2):
a = (y2 - y1) / (x2 - x1)
Wyraz Wolny (b)
Wyraz wolny b określa punkt, w którym prosta przecina oś OY. Punkt przecięcia ma współrzędne (0, b). Inaczej mówiąc, b to wartość funkcji dla x = 0.
Zadania i Rozwiązania
Zadanie 1: Wyznaczanie wzoru funkcji liniowej
Treść: Wyznacz wzór funkcji liniowej, której wykres przechodzi przez punkty A(1, 3) i B(2, 5).
Rozwiązanie:
1. Podstawiamy współrzędne punktów A i B do ogólnego wzoru funkcji liniowej:
- 3 = a * 1 + b
- 5 = a * 2 + b
2. Otrzymujemy układ równań:
{ 3 = a + b
{ 5 = 2a + b
3. Rozwiązujemy układ równań. Możemy odjąć pierwsze równanie od drugiego:
5 - 3 = 2a - a + b - b => 2 = a
4. Wstawiamy wartość a do jednego z równań, np. do pierwszego:
3 = 2 + b => b = 1
5. Otrzymujemy a = 2 i b = 1. Zatem wzór funkcji liniowej to:
f(x) = 2x + 1
Zadanie 2: Badanie monotoniczności funkcji
Treść: Określ, czy funkcja liniowa f(x) = -3x + 7 jest rosnąca, malejąca czy stała.
Rozwiązanie:
Współczynnik kierunkowy funkcji to a = -3. Ponieważ a < 0, funkcja jest malejąca.
Zadanie 3: Znajdowanie miejsca zerowego funkcji
Treść: Znajdź miejsce zerowe funkcji liniowej f(x) = x - 4.
Rozwiązanie:
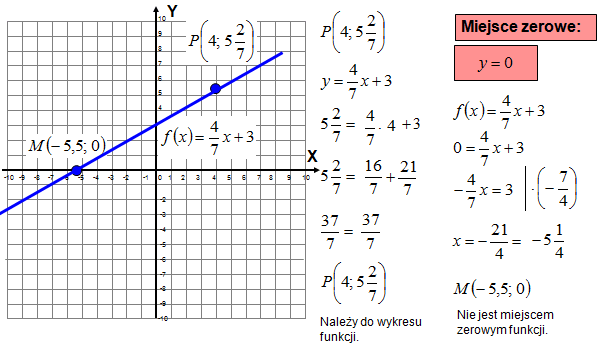
Miejsce zerowe to wartość x, dla której f(x) = 0. Zatem:
0 = x - 4 => x = 4
Miejsce zerowe funkcji to x = 4.
Zadanie 4: Równoległość i prostopadłość prostych
Treść: Sprawdź, czy proste o równaniach f(x) = 2x + 3 i g(x) = -0.5x + 1 są prostopadłe.
Rozwiązanie:
Dwie proste są prostopadłe, gdy iloczyn ich współczynników kierunkowych wynosi -1. Współczynnik kierunkowy pierwszej prostej to a1 = 2, a drugiej to a2 = -0.5.
a1 * a2 = 2 * (-0.5) = -1
Zatem proste są prostopadłe.
Zadanie 5: Prosta równoległa przechodząca przez punkt
Treść: Znajdź równanie prostej równoległej do prostej y = 3x - 2, która przechodzi przez punkt P(1, 5).
Rozwiązanie:
Proste równoległe mają taki sam współczynnik kierunkowy. Zatem szukana prosta ma współczynnik kierunkowy a = 3. Jej równanie ma postać:
y = 3x + b
Podstawiamy współrzędne punktu P(1, 5) do równania, aby wyznaczyć b:
5 = 3 * 1 + b => b = 2
Zatem równanie szukanej prostej to:
y = 3x + 2
Zadanie 6: Interpretacja współczynników w kontekście praktycznym
Treść: Koszt produkcji pewnego produktu opisuje funkcja liniowa K(x) = 5x + 100, gdzie x to liczba wyprodukowanych sztuk, a K(x) to koszt w złotych. Zinterpretuj współczynniki tej funkcji.
Rozwiązanie:
- a = 5: Koszt wyprodukowania jednej dodatkowej sztuki produktu wynosi 5 zł. Jest to koszt zmienny na jedną sztukę.
- b = 100: Koszt stały (niezależny od liczby wyprodukowanych sztuk) wynosi 100 zł. Są to np. koszty wynajmu hali, opłaty za energię, etc.
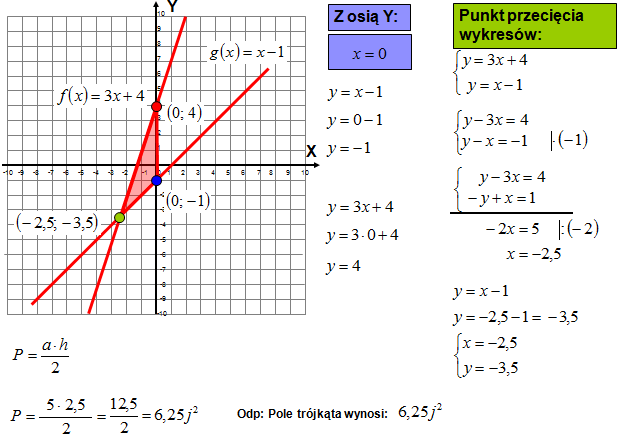
Zadanie 7: Znajdowanie punktu przecięcia dwóch prostych
Treść: Znajdź punkt przecięcia prostych o równaniach y = x + 1 oraz y = -2x + 4.
Rozwiązanie:
W punkcie przecięcia obie proste mają takie same wartości x i y. Zatem możemy przyrównać prawe strony równań:
x + 1 = -2x + 4
3x = 3 => x = 1
Podstawiamy x = 1 do jednego z równań, aby znaleźć y:
y = 1 + 1 = 2
Punkt przecięcia prostych to (1, 2).
Zadanie 8: Funkcja liniowa w modelowaniu zjawisk
Treść: Temperatura powietrza spada liniowo wraz z wysokością. Na poziomie morza temperatura wynosi 25°C, a na wysokości 1000 m temperatura wynosi 19°C. Znajdź wzór funkcji opisującej zależność temperatury od wysokości.
Rozwiązanie:
Niech T(h) oznacza temperaturę na wysokości h. Mamy dwa punkty: (0, 25) i (1000, 19).
Współczynnik kierunkowy a obliczamy:
a = (19 - 25) / (1000 - 0) = -6 / 1000 = -0.006
Wyraz wolny b to temperatura na poziomie morza, czyli b = 25.
Zatem wzór funkcji to:
T(h) = -0.006h + 25
Zadanie 9: Znajdowanie równania prostej, znając jej nachylenie i punkt
Treść: Znajdź równanie prostej, która ma nachylenie 2 i przechodzi przez punkt (3, 1).
Rozwiązanie:
Znamy współczynnik kierunkowy a = 2, więc równanie prostej ma postać:
y = 2x + b
Podstawiamy współrzędne punktu (3, 1) do równania:
1 = 2 * 3 + b => 1 = 6 + b => b = -5
Zatem równanie prostej to:
y = 2x - 5
Zadanie 10: Analiza graficzna funkcji liniowej
Treść: Na rysunku przedstawiony jest wykres funkcji liniowej. Odczytaj z wykresu współczynnik kierunkowy i wyraz wolny, a następnie napisz wzór funkcji.
Rozwiązanie (Założenia): Załóżmy, że na wykresie widzimy prostą przechodzącą przez punkty (0, -1) i (2, 3).
- Wyraz wolny (b): Z wykresu odczytujemy, że prosta przecina oś OY w punkcie (0, -1). Zatem b = -1.
- Współczynnik kierunkowy (a): Obliczamy go, korzystając z dwóch punktów na prostej: (0, -1) i (2, 3). a = (3 - (-1)) / (2 - 0) = 4 / 2 = 2.
Wzór funkcji liniowej to:
f(x) = 2x - 1
Zastosowania w praktyce
Funkcje liniowe znajdują szerokie zastosowanie w wielu dziedzinach życia:
- Ekonomia: Modelowanie kosztów, przychodów, zysków.
- Fizyka: Opisywanie ruchu jednostajnego.
- Informatyka: Algorytmy liniowe, analiza danych.
- Statystyka: Regresja liniowa.
- Codzienne życie: Przeliczanie walut, obliczanie kosztów przejazdu taksówką (często koszt początkowy + koszt za kilometr).
Na przykład, koszt przejazdu taksówką może być modelowany funkcją liniową, gdzie wyraz wolny reprezentuje opłatę początkową, a współczynnik kierunkowy – opłatę za przejechany kilometr.
Podsumowanie
Zrozumienie funkcji liniowej jest fundamentalne dla dalszej nauki matematyki i jej zastosowań. Umiejętność wyznaczania wzoru funkcji, badania jej monotoniczności, znajdowania miejsc zerowych, analizowania wzajemnego położenia prostych oraz interpretacji współczynników pozwala na rozwiązywanie różnorodnych problemów matematycznych i praktycznych. Kluczowe jest regularne rozwiązywanie zadań, aby utrwalić wiedzę i nabyć wprawę w posługiwaniu się funkcjami liniowymi.
Zachęcamy do dalszej eksploracji tematu funkcji liniowych, rozwiązywania dodatkowych zadań i szukania zastosowań w otaczającym nas świecie. Ćwiczenie czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz koncepcję funkcji liniowej i będziesz w stanie poradzić sobie z bardziej złożonymi problemami.