Funkcja Kwadratowa Sprawdzian Liceum Nowa Era

Hej! Zaraz czeka Cię sprawdzian z funkcji kwadratowej. Bez obaw, ogarniemy to razem! Skupmy się na najważniejszych zagadnieniach, żebyś na teście czuł się pewnie i swobodnie.

Postać ogólna, kanoniczna i iloczynowa

Funkcja kwadratowa w postaci ogólnej wygląda tak: f(x) = ax² + bx + c. Pamiętaj, że a nie może być równe zero! Współczynnik a decyduje o kierunku ramion paraboli (góra/dół) oraz o jej "szerokości". Zwróć na to uwagę.

Postać kanoniczna to: f(x) = a(x - p)² + q. Współrzędne wierzchołka paraboli to (p, q). Dzięki tej postaci od razu widzisz przesunięcie paraboli względem osi x i y. Umiejętność przejścia z postaci ogólnej do kanonicznej jest kluczowa.

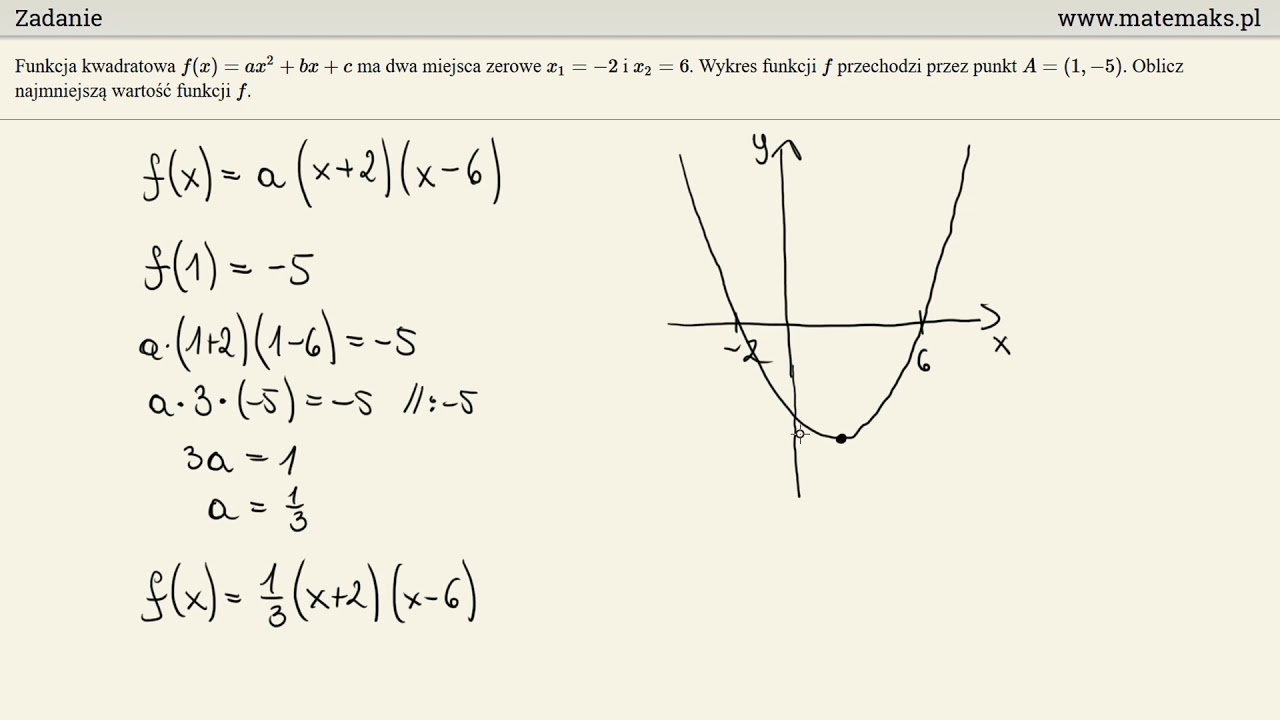
Jeśli funkcja ma miejsca zerowe, to możemy zapisać ją w postaci iloczynowej: f(x) = a(x - x₁)(x - x₂), gdzie x₁ i x₂ to miejsca zerowe. Pamiętaj o współczynniku a na początku. Brak tego współczynnika to częsty błąd.

Obliczanie delty (Δ) i miejsc zerowych

Delta (Δ) to podstawa! Wzór: Δ = b² - 4ac. To od niej zależy, ile miejsc zerowych ma funkcja. Pamiętaj o kolejności wykonywania działań.

Jeśli Δ > 0, funkcja ma dwa miejsca zerowe. Obliczysz je ze wzorów: x₁ = (-b - √Δ) / 2a oraz x₂ = (-b + √Δ) / 2a. Nie pomyl wzorów!

Jeśli Δ = 0, funkcja ma jedno miejsce zerowe (wierzchołek dotyka osi x). Wtedy: x₀ = -b / 2a. To jest też współrzędna p wierzchołka.

Jeśli Δ < 0, funkcja nie ma miejsc zerowych. Parabola nie przecina osi x.

Wierzchołek paraboli

Wierzchołek paraboli to bardzo ważny punkt. Jego współrzędne to (p, q). Możemy obliczyć je ze wzorów: p = -b / 2a oraz q = -Δ / 4a. Zapamiętaj te wzory!

Alternatywnie, jeśli masz postać kanoniczną, to odczytujesz p i q bezpośrednio. Wierzchołek to punkt, w którym funkcja osiąga wartość najmniejszą (dla a > 0) lub największą (dla a < 0). Pamiętaj o tym przy rozwiązywaniu zadań optymalizacyjnych.

Nierówności kwadratowe

Rozwiązywanie nierówności kwadratowych zaczyna się od znalezienia miejsc zerowych. Następnie rysujesz schematyczny wykres paraboli (ramiona w górę lub w dół, w zależności od znaku a). Ostatni krok to odczytanie przedziałów, w których funkcja spełnia nierówność. Ważne jest aby pamiętać o rodzaju nierówności (ostra, nieostra) i czy krańce przedziału należą do rozwiązania.

Podsumowanie

Pamiętaj o wzorach na deltę, miejsca zerowe i wierzchołek. Przećwicz zamianę postaci funkcji. Zrozum, jak współczynnik a wpływa na wykres. Powodzenia na sprawdzianie! Dasz radę!