Funkcja Kwadratowa Nowa Era Sprawdzian Liceum

Funkcja Kwadratowa, czyli funkcja stopnia drugiego, to funkcja, którą możemy zapisać w postaci ogólnej: f(x) = ax² + bx + c, gdzie a, b, c są stałymi liczbami rzeczywistymi, a a ≠ 0. Sprawdzian z tego tematu w liceum Nowa Era obejmuje zazwyczaj znajomość postaci funkcji, jej własności (miejsca zerowe, wierzchołek, oś symetrii, monotoniczność), rozwiązywanie równań i nierówności kwadratowych oraz interpretację graficzną – paraboli.

Krok 1: Rozpoznawanie Funkcji Kwadratowej

Pierwszym krokiem jest rozpoznanie, czy dana funkcja jest rzeczywiście kwadratowa. Kluczowe jest obecność składnika z x², a współczynnik przy nim (a) nie może być zerem. Na przykład: f(x) = 2x² - 3x + 1 jest funkcją kwadratową (a=2, b=-3, c=1). Natomiast f(x) = 3x + 5 nie jest, bo brakuje składnika z x². Sprawdzaj uważnie, czy najwyższa potęga x wynosi 2.

Krok 2: Postacie Funkcji Kwadratowej

Funkcję kwadratową możemy zapisać w trzech postaciach:

Postać ogólna: f(x) = ax² + bx + c (jak wspomniano wcześniej)
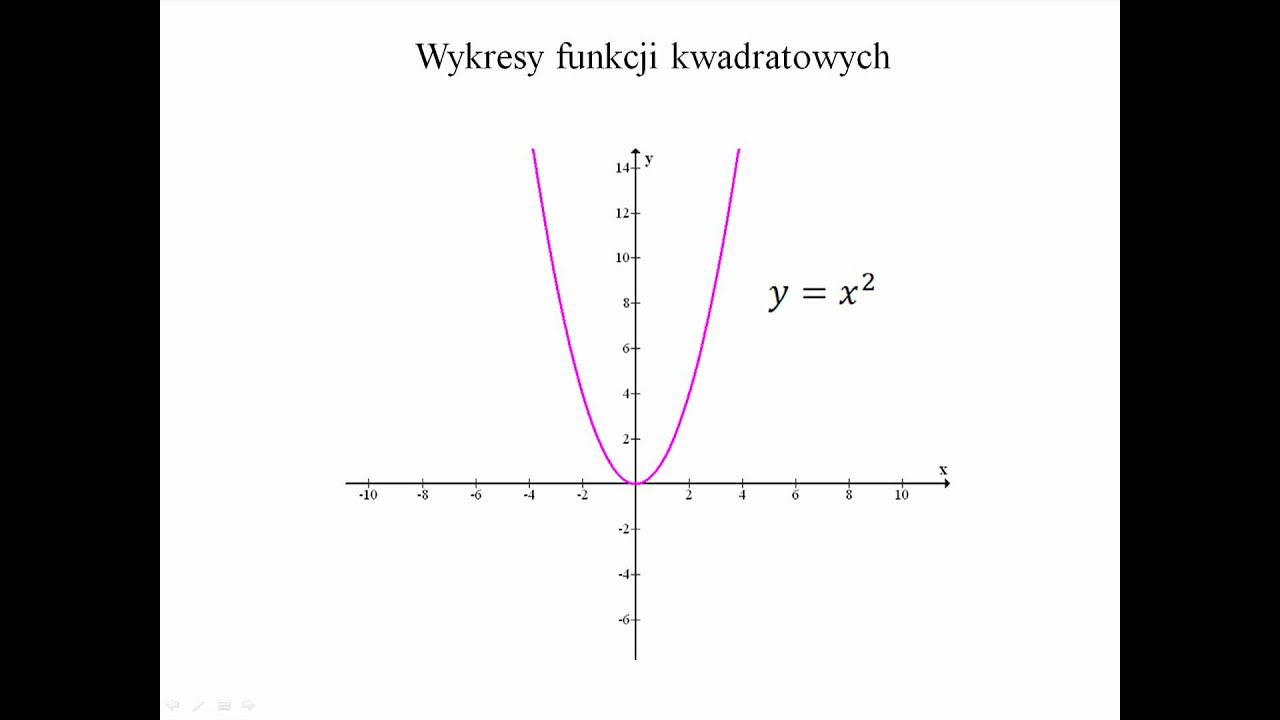
Postać kanoniczna: f(x) = a(x - p)² + q, gdzie (p, q) to współrzędne wierzchołka paraboli. Wierzchołek to punkt, w którym funkcja osiąga maksimum lub minimum.
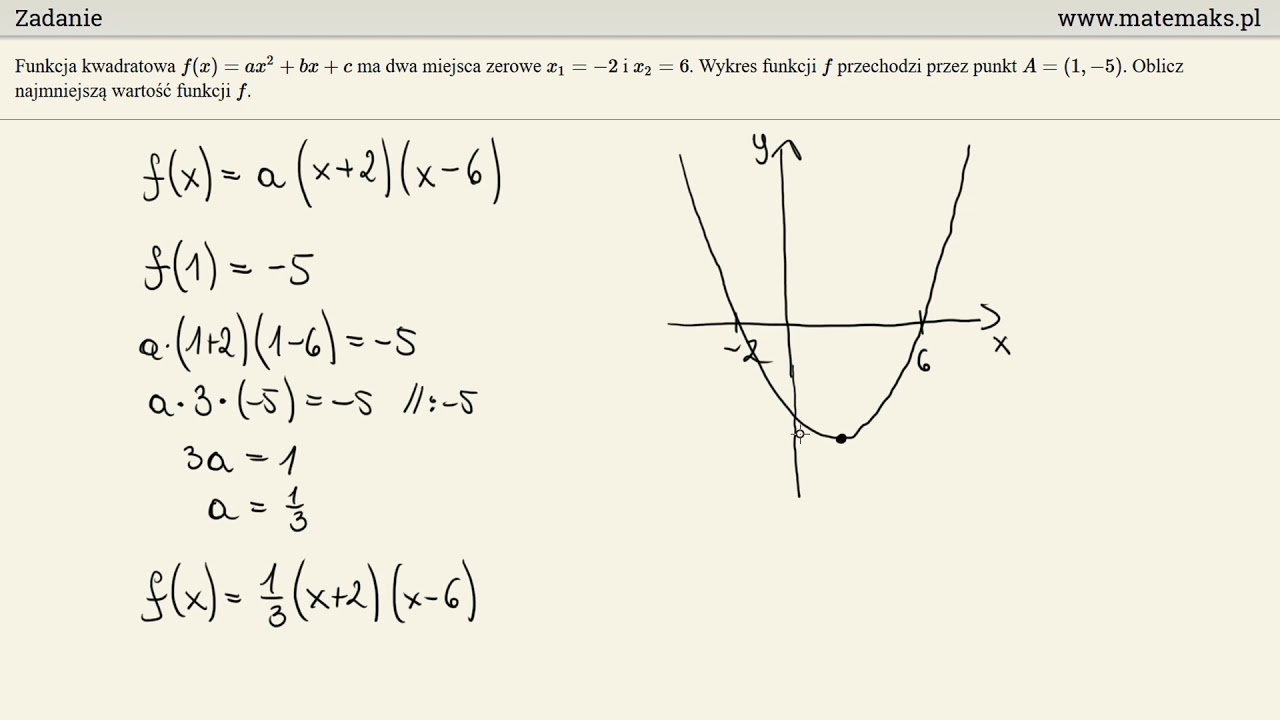
Postać iloczynowa: f(x) = a(x - x₁)(x - x₂), gdzie x₁ i x₂ to miejsca zerowe funkcji. Ta postać istnieje tylko, gdy delta (Δ = b² - 4ac) jest większa lub równa 0.

Znajomość tych postaci pozwala na szybkie odczytywanie istotnych informacji o funkcji.

Krok 3: Obliczanie Wyróżnika (Delta) i Miejsc Zerowych

Delta (Δ) pozwala określić, ile funkcja ma miejsc zerowych:

Δ > 0: funkcja ma dwa różne miejsca zerowe: x₁ = (-b - √Δ) / 2a oraz x₂ = (-b + √Δ) / 2a
Δ = 0: funkcja ma jedno miejsce zerowe (pierwiastek podwójny): x = -b / 2a
Δ < 0: funkcja nie ma miejsc zerowych (parabola nie przecina osi OX)

Przykład: dla funkcji f(x) = x² - 4x + 3, mamy Δ = (-4)² - 4 * 1 * 3 = 4. Zatem x₁ = (4 - √4) / 2 = 1 i x₂ = (4 + √4) / 2 = 3.

Krok 4: Określanie Wierzchołka Paraboli

Współrzędne wierzchołka (p, q) obliczamy ze wzorów:

p = -b / 2a
q = -Δ / 4a

Dla naszej przykładowej funkcji f(x) = x² - 4x + 3, wierzchołek ma współrzędne p = -(-4) / 2 = 2 oraz q = -4 / 4 = -1, czyli (2, -1).

Praktyczne Zastosowania

Funkcja kwadratowa jest używana w wielu dziedzinach, na przykład:

Fizyka: opisuje ruch ciała wyrzuconego pod kątem (tor paraboli). Obliczanie maksymalnego zasięgu rzutu.
Ekonomia: modelowanie kosztów i przychodów, optymalizacja zysku. Znalezienie punktu, w którym zysk jest największy.

Zrozumienie funkcji kwadratowej jest kluczowe nie tylko na sprawdzianie, ale i w praktycznych zastosowaniach.