Fizyka Kinematyka Zadania Klasa 7

Witajcie, młodzi adepci nauki! Przygotujcie się na fascynującą podróż w świat kinematyki – działu fizyki, który opisuje ruch ciał, nie wnikając w przyczyny, które ten ruch wywołują. Kinematyka jest fundamentem dla zrozumienia wielu zjawisk zachodzących wokół nas, od codziennych, jak jazda na rowerze, po bardziej złożone, jak ruch planet.

Podstawowe Pojęcia Kinematyki

Położenie i Układ Odniesienia

Pierwszym krokiem do zrozumienia ruchu jest określenie położenia ciała. To, gdzie coś się znajduje, zawsze określamy względem czegoś innego, czyli względem układu odniesienia. Wyobraźcie sobie, że siedzicie w pociągu. Dla pasażera siedzącego obok Was, Wasze położenie się nie zmienia. Natomiast dla osoby stojącej na peronie, Wasze położenie ciągle się zmienia wraz z ruchem pociągu.

Układ odniesienia najczęściej stanowią osie współrzędnych (np. x, y, z). Położenie ciała opisujemy podając jego współrzędne w danym układzie odniesienia. Na przykład, piłka leżąca na boisku może mieć współrzędne (5, 2) w metrach, względem rogu boiska, który wybraliśmy jako początek układu współrzędnych.

Przemieszczenie i Droga

Przemieszczenie to wektor, który łączy położenie początkowe z położeniem końcowym ciała. Ważna jest kierunek i wartość tego wektora. Z kolei droga to długość toru, po którym poruszało się ciało. Przemieszczenie i droga są równe tylko w przypadku ruchu prostoliniowego w jednym kierunku.

Wyobraźcie sobie, że idziecie z domu do sklepu oddalonego o 100 metrów, a następnie wracacie do domu. Droga, jaką przebyliście, wynosi 200 metrów. Natomiast Wasze przemieszczenie wynosi 0 metrów, ponieważ wróciliście do punktu wyjścia.

Prędkość

Prędkość informuje nas, jak szybko zmienia się położenie ciała w czasie. Mamy dwa rodzaje prędkości: średnią i chwilową.

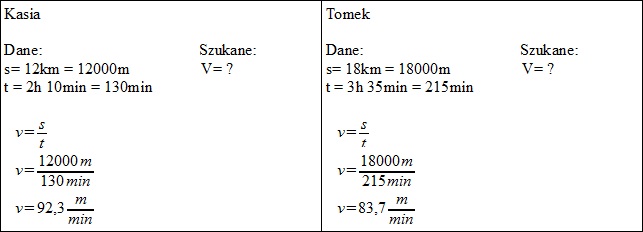
Prędkość średnia to iloraz całkowitego przemieszczenia przez całkowity czas trwania ruchu. Możemy ją obliczyć ze wzoru: v_śr = Δs / Δt, gdzie Δs to przemieszczenie, a Δt to czas.

Prędkość chwilowa to prędkość ciała w danej chwili czasu. Można ją sobie wyobrazić jako prędkość średnią, mierzoną w bardzo krótkim przedziale czasu. Prędkościomierz w samochodzie wskazuje właśnie prędkość chwilową.

Prędkość jest wielkością wektorową, co oznacza, że ma kierunek i wartość (szybkość). Szybkość to wartość prędkości, czyli informacja o tym, jak szybko się poruszamy, bez względu na kierunek.

Przykład: Samochód przejechał 200 km w 2 godziny. Jego prędkość średnia wynosi 100 km/h. Nie oznacza to, że przez całą podróż jechał z tą samą prędkością. Mógł jechać szybciej na autostradzie i wolniej w mieście.

Przyspieszenie

Przyspieszenie opisuje, jak szybko zmienia się prędkość ciała w czasie. Podobnie jak prędkość, przyspieszenie może być średnie lub chwilowe.

Przyspieszenie średnie to iloraz zmiany prędkości przez czas, w którym ta zmiana nastąpiła: a_śr = Δv / Δt, gdzie Δv to zmiana prędkości, a Δt to czas.

Przyspieszenie chwilowe to przyspieszenie ciała w danej chwili czasu.

Przyspieszenie jest również wielkością wektorową. Jeśli przyspieszenie ma taki sam kierunek jak prędkość, ciało przyspiesza. Jeśli ma przeciwny kierunek, ciało zwalnia (mówimy wtedy o opóźnieniu).

Przykład: Samochód zwiększa swoją prędkość z 0 km/h do 100 km/h w 10 sekund. Jego średnie przyspieszenie wynosi około 2.78 m/s². Oznacza to, że w każdej sekundzie jego prędkość wzrasta o 2.78 m/s.

Rodzaje Ruchu

Ruch Jednostajny Prostoliniowy

To najprostszy rodzaj ruchu. Ciało porusza się po linii prostej ze stałą prędkością (przyspieszenie jest równe zero). Przykłady: jadący ze stałą prędkością pociąg na prostym odcinku torów, spadający kropla deszczu (po pewnym czasie, kiedy opór powietrza się ustali).

Równania opisujące ruch jednostajny prostoliniowy:

v = const. (prędkość stała)
a = 0 (przyspieszenie równe zero)
s = vt (droga = prędkość * czas)

Ruch Jednostajnie Przyspieszony Prostoliniowy

Ciało porusza się po linii prostej ze stałym przyspieszeniem. Przykłady: spadające swobodnie ciało (pomijając opór powietrza), samochód ruszający ze świateł z stałym przyspieszeniem.

Równania opisujące ruch jednostajnie przyspieszony prostoliniowy:

a = const. (przyspieszenie stałe)
v = v₀ + at (prędkość = prędkość początkowa + przyspieszenie * czas)
s = v₀t + (at²)/2 (droga = prędkość początkowa * czas + (przyspieszenie * czas²)/2)

Gdzie v₀ to prędkość początkowa.

Ruch Jednostajnie Opóźniony Prostoliniowy

Ciało porusza się po linii prostej ze stałym opóźnieniem (czyli przyspieszeniem o zwrocie przeciwnym do prędkości). Przykłady: samochód hamujący na prostej drodze, rzucona do góry piłka (podczas wznoszenia się).

Równania opisujące ruch jednostajnie opóźniony prostoliniowy są podobne do tych dla ruchu przyspieszonego, ale przyspieszenie ma znak ujemny:

a = const. (przyspieszenie stałe, ale ujemne)
v = v₀ - at (prędkość = prędkość początkowa - przyspieszenie * czas)
s = v₀t - (at²)/2 (droga = prędkość początkowa * czas - (przyspieszenie * czas²)/2)

Rozwiązywanie Zadań z Kinematyki

Kluczem do rozwiązywania zadań z kinematyki jest:

Zrozumienie treści zadania: Przeczytaj uważnie zadanie i upewnij się, że rozumiesz, co jest dane, a co należy obliczyć.
Sporządzenie rysunku: Narysuj schemat sytuacji. Oznacz położenia, prędkości, przyspieszenia, siły (jeśli występują).
Wybór układu odniesienia: Wybierz układ odniesienia, który uprości rozwiązanie zadania. Określ kierunki osi współrzędnych.
Wypisanie danych i szukanych: Zapisz wszystkie dane liczbowe i wielkości, które masz obliczyć.
Dobór odpowiednich wzorów: Wybierz wzory, które wiążą dane wielkości z szukanymi.
Rozwiązanie równań: Rozwiąż równania, aby obliczyć szukane wielkości.
Sprawdzenie jednostek: Upewnij się, że wszystkie wielkości mają odpowiednie jednostki. Używaj jednostek układu SI (metr, sekunda, kilogram).
Analiza wyniku: Sprawdź, czy otrzymany wynik ma sens fizyczny. Zastanów się, czy jest realistyczny.

Przykładowe Zadanie

Treść: Samochód rusza z miejsca i przyspiesza jednostajnie przez 5 sekund, osiągając prędkość 20 m/s. Oblicz przyspieszenie samochodu i drogę, jaką przebył w tym czasie.

Rozwiązanie:

Dane: v₀ = 0 m/s, v = 20 m/s, t = 5 s
Szukane: a = ?, s = ?
Wzory:
- v = v₀ + at
- s = v₀t + (at²)/2
Obliczenia:
- a = (v - v₀) / t = (20 m/s - 0 m/s) / 5 s = 4 m/s²
- s = (0 m/s * 5 s) + (4 m/s² * (5 s)²) / 2 = 50 m
Odpowiedź: Przyspieszenie samochodu wynosi 4 m/s², a droga, jaką przebył, wynosi 50 m.

Kinematyka w Życiu Codziennym

Kinematyka otacza nas z każdej strony. Od projektowania pojazdów i budynków, po analizę sportowych wyczynów. Znajomość podstaw kinematyki pozwala lepiej rozumieć świat i przewidywać zachowanie ciał w ruchu.

Przykłady:

Projektowanie samochodów: Inżynierowie wykorzystują kinematykę do obliczania czasu hamowania, przyspieszenia i stabilności pojazdu.
Sport: Trenerzy analizują ruch sportowców, aby poprawić ich technikę i efektywność. Na przykład, analizując trajektorię lotu piłki w koszykówce można zoptymalizować rzut.
Animacje komputerowe: Kinematyka jest używana do tworzenia realistycznych ruchów postaci w grach komputerowych i filmach.
Medycyna: Analiza chodu pacjentów pomaga w diagnozowaniu i leczeniu problemów z ruchem.

Podsumowanie

Kinematyka to fascynujący dział fizyki, który opisuje ruch ciał. Zrozumienie podstawowych pojęć, takich jak położenie, przemieszczenie, prędkość i przyspieszenie, oraz znajomość rodzajów ruchu (jednostajnego, przyspieszonego, opóźnionego) jest kluczowe do rozwiązywania zadań i zrozumienia zjawisk zachodzących wokół nas. Pamiętajcie, że praktyka czyni mistrza. Rozwiązujcie jak najwięcej zadań, a kinematyka stanie się dla Was prosta i zrozumiała!

Zachęcam do dalszego zgłębiania wiedzy z zakresu fizyki! Spróbujcie sami wymyślać i rozwiązywać zadania. Obserwujcie ruchy ciał w otaczającym Was świecie i starajcie się je opisywać za pomocą pojęć z kinematyki. Powodzenia!