Figury Przestrzenne Test Kl 6

Zrozumienie figur przestrzennych jest kluczowe w matematyce i ma ogromne znaczenie w naszym codziennym życiu. W klasie 6 uczniowie zaczynają poznawać podstawowe figury geometryczne w trzech wymiarach. Test z figur przestrzennych dla klasy 6 ma na celu sprawdzenie, czy uczniowie rozumieją właściwości, wzory i zastosowania tych figur. Niniejszy artykuł ma na celu przybliżenie tego tematu, omówienie kluczowych aspektów, które pojawiają się na teście, oraz pokazanie, jak ta wiedza przydaje się w praktyce.

Podstawowe Figury Przestrzenne

Prostopadłościan i Sześcian

Prostopadłościan to figura przestrzenna, która ma sześć ścian, a każda ściana jest prostokątem. Sześcian jest szczególnym przypadkiem prostopadłościanu, gdzie wszystkie ściany są kwadratami. Na teście często pojawiają się zadania związane z obliczaniem pola powierzchni i objętości tych figur.

Pole powierzchni prostopadłościanu obliczamy, sumując pola wszystkich jego ścian. Wzór na pole powierzchni prostopadłościanu o krawędziach a, b, i c to: 2(ab + bc + ac). Natomiast pole powierzchni sześcianu o krawędzi a, to 6a².

Objętość prostopadłościanu obliczamy, mnożąc długości jego krawędzi: a * b * c. Objętość sześcianu to po prostu a³, gdzie a to długość krawędzi.

Przykład: Wyobraźmy sobie pudełko na buty (prostopadłościan) o wymiarach 30 cm x 20 cm x 10 cm. Pole powierzchni tego pudełka wynosi 2(30*20 + 20*10 + 30*10) = 2(600 + 200 + 300) = 2200 cm². Objętość tego pudełka to 30 * 20 * 10 = 6000 cm³.

Graniastosłupy

Graniastosłup to figura przestrzenna, która ma dwie podstawy będące identycznymi wielokątami oraz ściany boczne będące prostokątami (lub równoległobokami). Ważne jest, aby odróżniać różne rodzaje graniastosłupów, takie jak graniastosłup trójkątny, czworokątny, pięciokątny, itd., w zależności od kształtu podstawy.

Pole powierzchni graniastosłupa obliczamy, sumując pola wszystkich ścian. Czyli: 2 * pole podstawy + pole powierzchni bocznej. Objętość graniastosłupa obliczamy, mnożąc pole podstawy przez wysokość graniastosłupa: pole podstawy * wysokość.

Przykład: Graniastosłup trójkątny ma podstawę w kształcie trójkąta o podstawie 5 cm i wysokości 4 cm. Wysokość graniastosłupa wynosi 10 cm. Pole podstawy trójkąta to (5 * 4) / 2 = 10 cm². Objętość graniastosłupa to 10 * 10 = 100 cm³.

Ostrosłupy

Ostrosłup to figura przestrzenna, która ma jedną podstawę będącą wielokątem oraz ściany boczne będące trójkątami zbiegającymi się w jednym punkcie, zwanym wierzchołkiem ostrosłupa. Podobnie jak w przypadku graniastosłupów, rozróżniamy ostrosłupy trójkątne, czworokątne, itp.

Pole powierzchni ostrosłupa obliczamy, sumując pole podstawy i pola wszystkich ścian bocznych. Objętość ostrosłupa obliczamy ze wzoru: (1/3) * pole podstawy * wysokość.

Przykład: Ostrosłup czworokątny ma podstawę w kształcie kwadratu o boku 6 cm. Wysokość ostrosłupa wynosi 8 cm. Pole podstawy to 6 * 6 = 36 cm². Objętość ostrosłupa to (1/3) * 36 * 8 = 96 cm³.

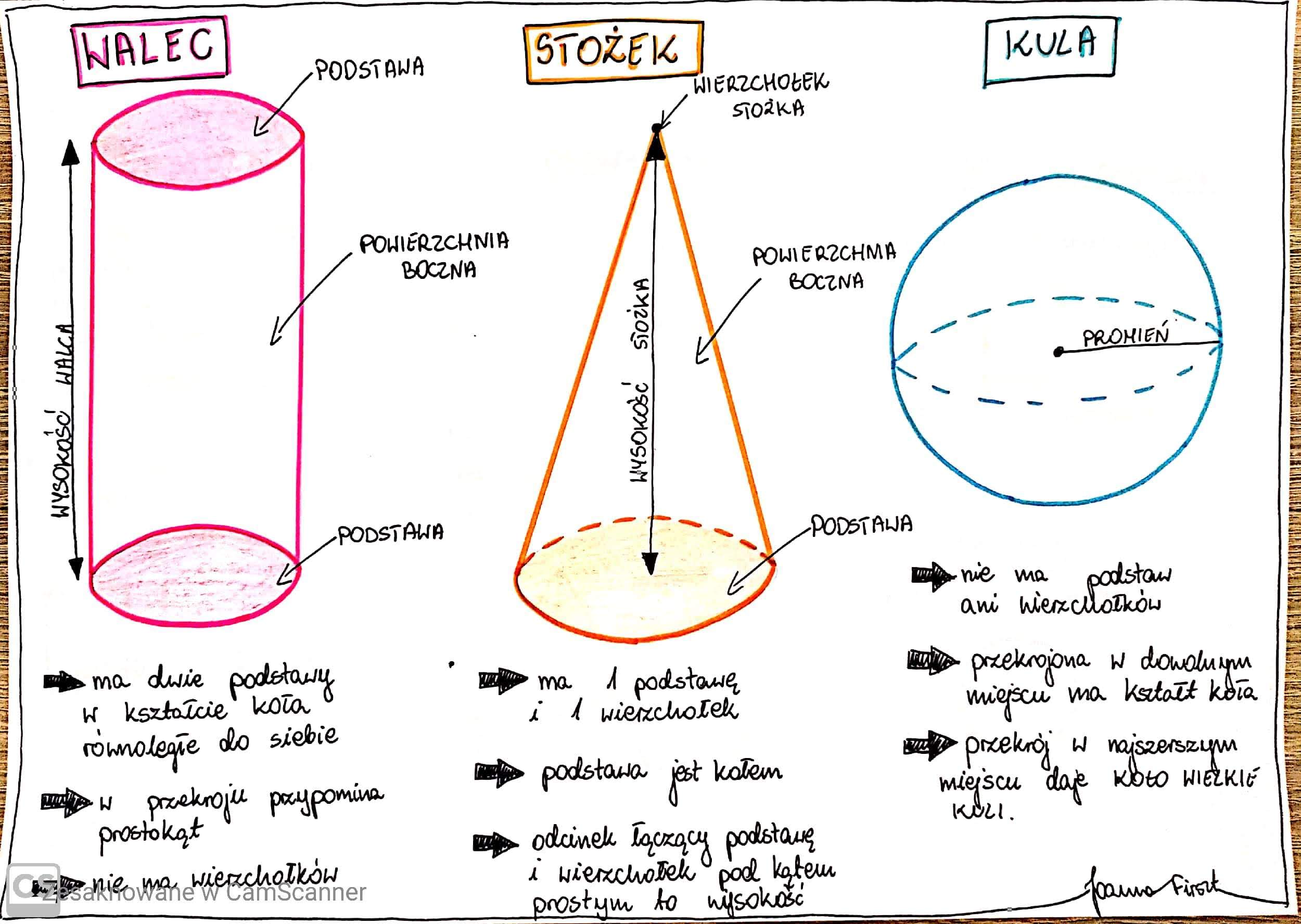
Walec, Stożek i Kula

Walec to figura przestrzenna, która ma dwie podstawy w kształcie kół połączone powierzchnią boczną, która po rozwinięciu tworzy prostokąt. Stożek ma jedną podstawę w kształcie koła i powierzchnię boczną, która zwęża się do wierzchołka. Kula to zbiór punktów w przestrzeni, które są w równej odległości od środka.

Pole powierzchni walca to 2 * pole podstawy + pole powierzchni bocznej, czyli 2πr² + 2πrh, gdzie r to promień podstawy, a h to wysokość walca. Objętość walca to pole podstawy * wysokość, czyli πr²h.

Pole powierzchni stożka to pole podstawy + pole powierzchni bocznej, czyli πr² + πrl, gdzie r to promień podstawy, a l to długość tworzącej stożka. Objętość stożka to (1/3) * pole podstawy * wysokość, czyli (1/3)πr²h.

Pole powierzchni kuli to 4πr², gdzie r to promień kuli. Objętość kuli to (4/3)πr³.

Przykład: Walec ma promień podstawy 3 cm i wysokość 7 cm. Pole powierzchni walca to 2π(3²) + 2π(3)(7) = 18π + 42π = 60π cm². Objętość walca to π(3²)(7) = 63π cm³.

Praktyczne Zastosowania Figur Przestrzennych

Wiedza o figurach przestrzennych jest niezwykle przydatna w wielu dziedzinach życia. Oto kilka przykładów:

Architektura i Budownictwo: Projektowanie budynków, obliczanie ilości materiałów budowlanych, wyznaczanie powierzchni i objętości pomieszczeń.
Inżynieria: Projektowanie maszyn, mostów, rurociągów. Obliczanie wytrzymałości konstrukcji.
Opakowania: Projektowanie opakowań o optymalnej objętości i kształcie, minimalizując zużycie materiałów.
Projektowanie Gier Komputerowych i Grafika 3D: Tworzenie realistycznych modeli trójwymiarowych obiektów.
Medycyna: Obliczanie objętości guzów nowotworowych, projektowanie implantów.

Przykład z życia: Architekt projektujący dom musi dokładnie obliczyć objętość pomieszczeń, aby dobrać odpowiedni system ogrzewania i wentylacji. Inżynier projektujący most musi uwzględnić obciążenia i naprężenia, aby zapewnić jego stabilność. Producent opakowań musi zaprojektować pudełko na pizzę, które będzie miało odpowiednią objętość i kształt, aby pizza się zmieściła i nie uległa uszkodzeniu.

Jak Przygotować Się do Testu?

Przygotowanie do testu z figur przestrzennych wymaga systematycznej nauki i rozwiązywania zadań. Oto kilka wskazówek:

Powtórz definicje i wzory: Upewnij się, że rozumiesz definicje wszystkich figur przestrzennych i znasz wzory na pole powierzchni i objętość.
Rozwiązuj zadania: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz, jak stosować wzory i jakie strategie rozwiązywania są skuteczne.
Korzystaj z materiałów edukacyjnych: Skorzystaj z podręcznika, zeszytu ćwiczeń, internetowych zasobów edukacyjnych.
Poproś o pomoc: Jeśli masz trudności z jakimś zagadnieniem, poproś o pomoc nauczyciela, rodzica lub kolegę.
Wyobraźnia przestrzenna: Trenuj swoją wyobraźnię przestrzenną, np. rysując figury przestrzenne, budując modele z klocków.

Pamiętaj: Najważniejsze jest zrozumienie koncepcji i logiczne myślenie, a nie tylko zapamiętywanie wzorów.

Typowe Zadania na Teście

Na teście z figur przestrzennych dla klasy 6 mogą pojawić się następujące typy zadań:

Obliczanie pola powierzchni i objętości: Zadania polegające na obliczeniu pola powierzchni i objętości różnych figur przestrzennych na podstawie podanych wymiarów.
Zadania tekstowe: Zadania, w których trzeba zastosować wiedzę o figurach przestrzennych do rozwiązania problemu praktycznego.
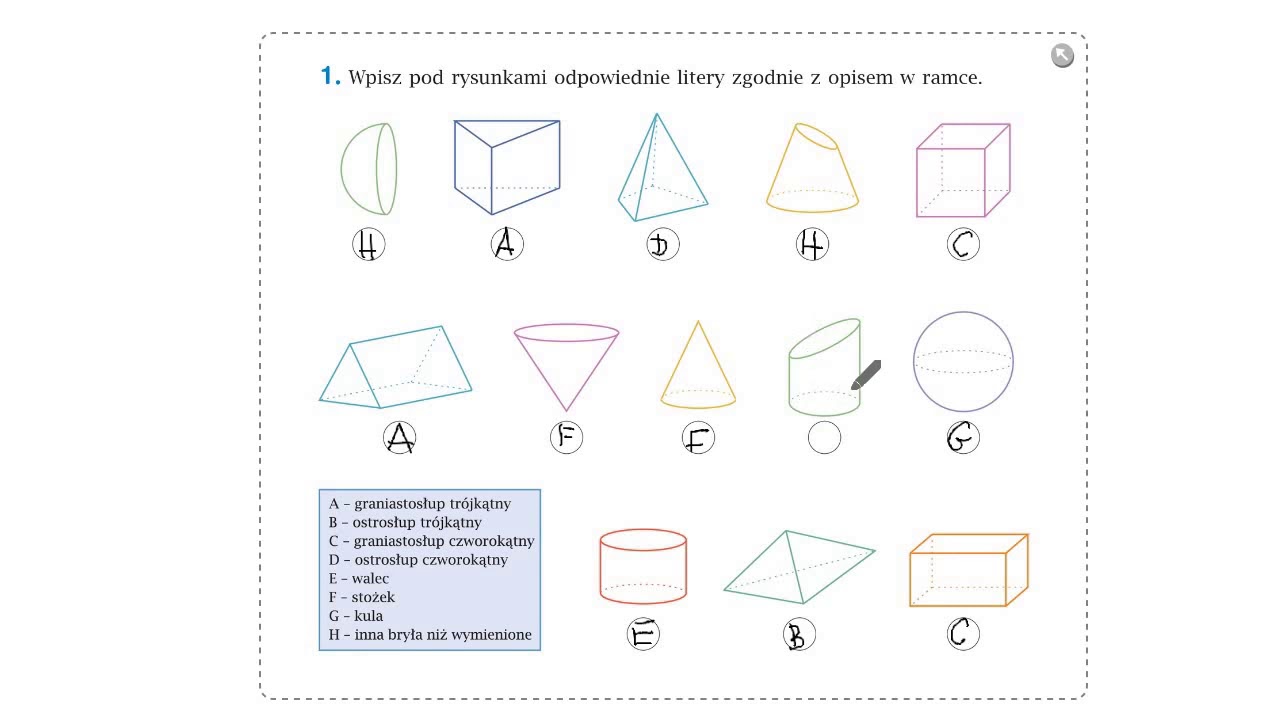
Rozpoznawanie figur przestrzennych: Zadania polegające na rozpoznawaniu figur przestrzennych na podstawie rysunków lub opisów.
Zadania na wyobraźnię przestrzenną: Zadania polegające na rozwiązywaniu problemów wymagających wyobraźni przestrzennej, np. określanie, jak wygląda figura przestrzenna po obróceniu lub rozłożeniu.
Przeliczanie jednostek: Zadania wymagające przeliczania jednostek długości, pola powierzchni i objętości.

Przykład: Oblicz objętość sześcianu o krawędzi 5 cm. Odpowiedź: 5³ = 125 cm³.

Przykład: Pokój ma wymiary 4 m x 3 m x 2.5 m. Ile litrów powietrza zmieści się w tym pokoju? Odpowiedź: 4 * 3 * 2.5 = 30 m³. 1 m³ = 1000 litrów, więc 30 m³ = 30000 litrów.

Podsumowanie

Zrozumienie figur przestrzennych jest fundamentalne dla dalszej nauki matematyki i wielu innych dziedzin. Przygotowanie do testu z tego zakresu wymaga systematycznej nauki, rozwiązywania zadań i rozwijania wyobraźni przestrzennej. Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć ten temat i przygotować się do testu. Powodzenia!