Figury Na Płaszczyźnie Sprawdzian Klasa 5 Matematyka Z Plusem Odpowiedzi

Uczniowie klasy 5, witam! Widzę, że zbliża się sprawdzian z figur na płaszczyźnie, a konkretnie "Matematyka z Plusem". Postaram się rozwiać wszelkie Wasze wątpliwości i usystematyzować wiedzę, abyście mogli podejść do tego sprawdzianu z pewnością siebie. Przygotowałem dla Was kompleksowe omówienie zagadnień, które najprawdopodobniej pojawią się na sprawdzianie. Skupimy się na definicjach, własnościach i sposobach obliczania parametrów różnych figur.

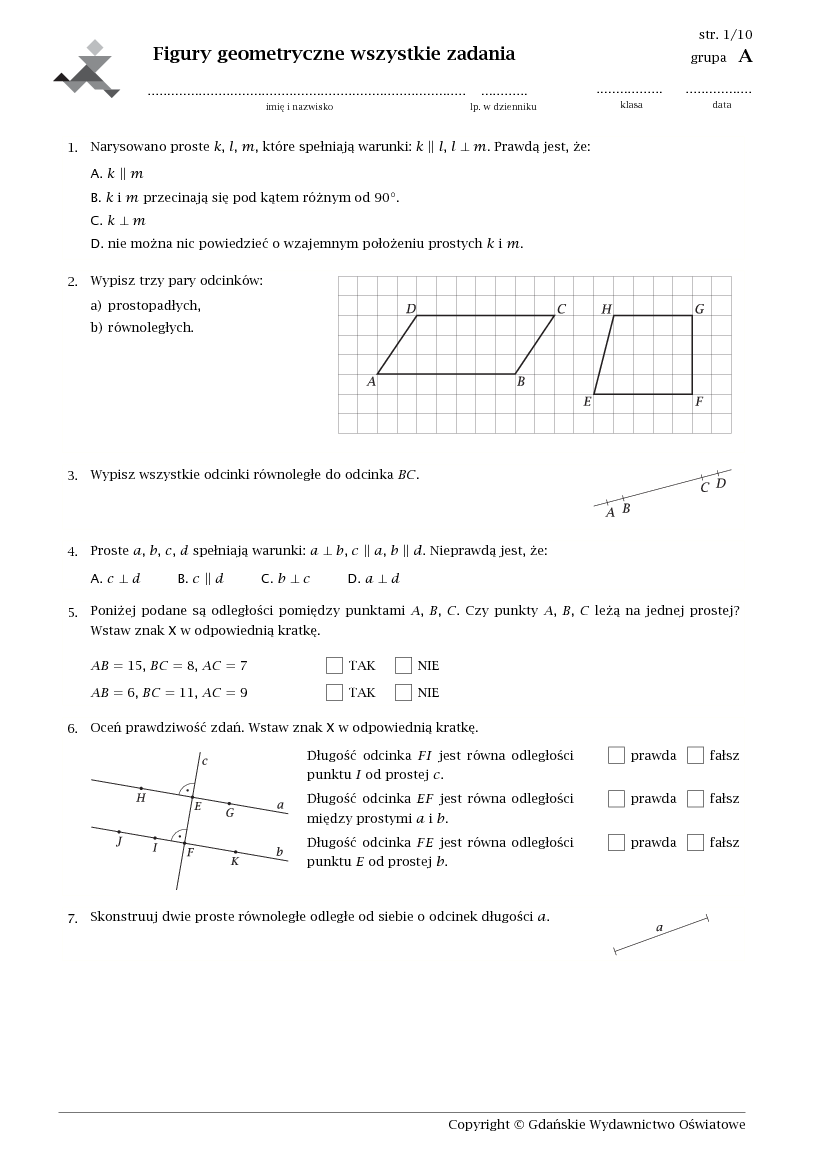
Zacznijmy od podstaw: Punkty, proste i odcinki. Punkt jest podstawowym elementem geometrii – nie ma wymiarów, a jedynie położenie. Prosta jest nieskończona w obu kierunkach i składa się z nieskończonej liczby punktów. Odcinek natomiast jest fragmentem prostej ograniczonym dwoma punktami – jego końcami. Pamiętajcie o oznaczeniach: punkt oznaczamy dużą literą (np. A), prostą małą literą (np. k), a odcinek dwoma dużymi literami oznaczającymi jego końce (np. AB) z kreską nad nimi.

Kolejnym ważnym elementem są kąty. Kąt to figura geometryczna utworzona przez dwie półproste wychodzące z jednego punktu, zwanego wierzchołkiem. Kąty mierzymy w stopniach. Mamy różne rodzaje kątów:

Kąt ostry – jego miara jest mniejsza niż 90 stopni.
Kąt prosty – jego miara wynosi dokładnie 90 stopni. Oznaczamy go małym kwadratem w wierzchołku.
Kąt rozwarty – jego miara jest większa niż 90 stopni, ale mniejsza niż 180 stopni.
Kąt półpełny – jego miara wynosi dokładnie 180 stopni.
Kąt pełny – jego miara wynosi 360 stopni.

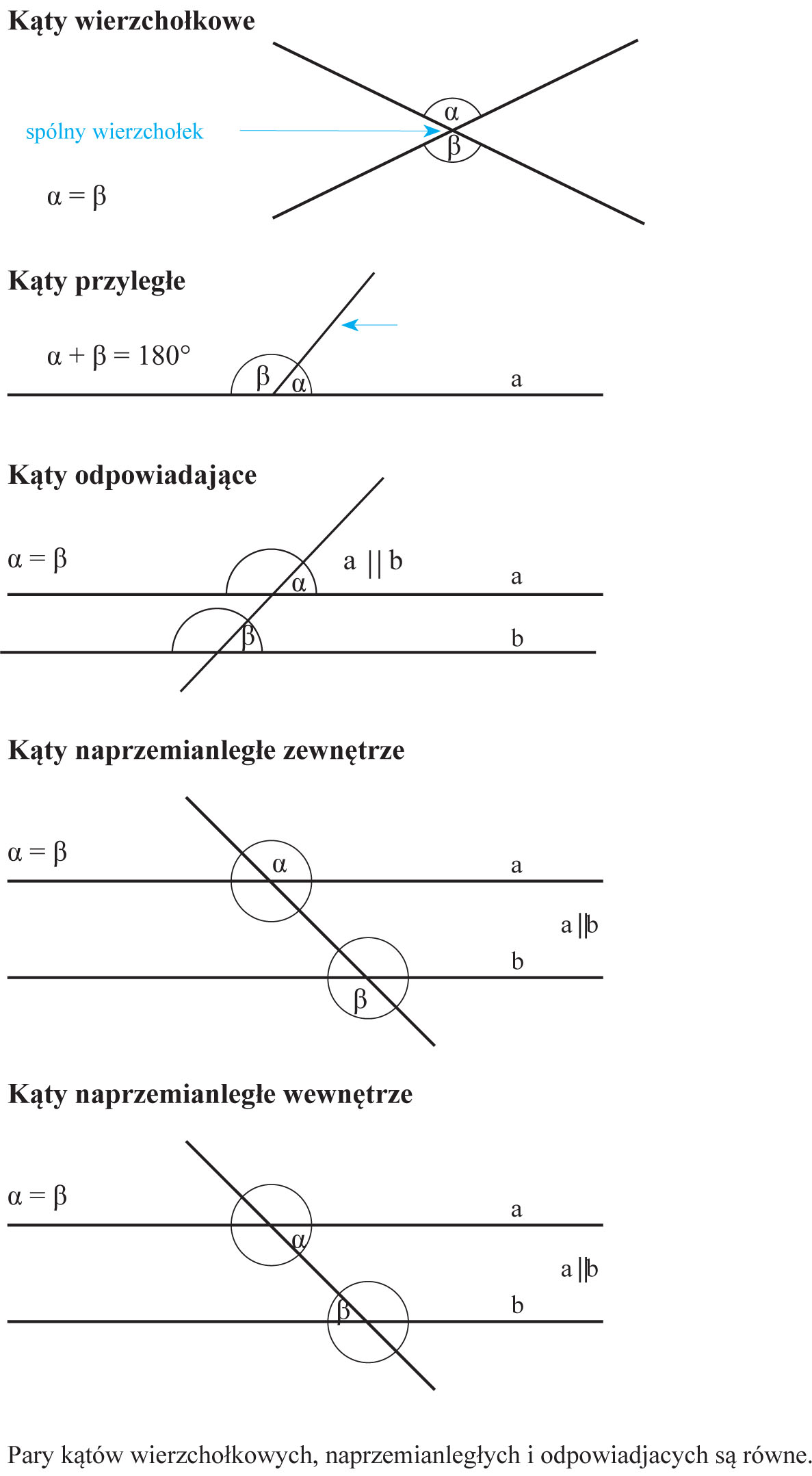
Pamiętajcie o kątach przyległych (które mają wspólne ramię i wierzchołek, a ich suma miar wynosi 180 stopni) oraz wierzchołkowych (które są parami równe).

Teraz przejdźmy do wielokątów. Wielokąt to figura geometryczna ograniczona łamaną zamkniętą. Wielokąty dzielimy ze względu na liczbę boków: trójkąty (3 boki), czworokąty (4 boki), pięciokąty (5 boków), sześciokąty (6 boków) itd. Każdy wielokąt ma wierzchołki i boki. Suma miar kątów wewnętrznych w trójkącie wynosi 180 stopni, a w czworokącie 360 stopni.

Skupmy się na trójkątach. Trójkąty dzielimy ze względu na długość boków na:

Trójkąt równoboczny – wszystkie boki są równe. Wszystkie kąty wewnętrzne mają miarę 60 stopni.
Trójkąt równoramienny – dwa boki są równe (ramiona). Kąty przy podstawie są równe.
Trójkąt różnoboczny – wszystkie boki mają różne długości.

Ze względu na miary kątów trójkąty dzielimy na:

Trójkąt ostrokątny – wszystkie kąty są ostre.
Trójkąt prostokątny – jeden z kątów jest prosty. Bok naprzeciwko kąta prostego nazywamy przeciwprostokątną, a pozostałe dwa boki to przyprostokątne.
Trójkąt rozwartokątny – jeden z kątów jest rozwarty.

Ważne jest, aby umieć obliczyć pole trójkąta. Podstawowy wzór to: P = (a * h) / 2, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę. W trójkącie prostokątnym pole można obliczyć również jako połowę iloczynu długości przyprostokątnych.

Następnie omówimy czworokąty. Do najważniejszych czworokątów należą:

Kwadrat – wszystkie boki są równe i wszystkie kąty są proste. Jego przekątne są równe, przecinają się pod kątem prostym i dzielą się na połowy.
Prostokąt – wszystkie kąty są proste, a przeciwległe boki są równe. Jego przekątne są równe i dzielą się na połowy.
Romb – wszystkie boki są równe, a przeciwległe kąty są równe. Jego przekątne przecinają się pod kątem prostym i dzielą się na połowy.
Równoległobok – przeciwległe boki są równoległe i równe, a przeciwległe kąty są równe. Jego przekątne dzielą się na połowy.
Trapez – ma co najmniej jedną parę boków równoległych (podstawy). Pozostałe boki nazywamy ramionami. Trapez, którego ramiona są równe, nazywamy trapezem równoramiennym. Trapez, który ma jeden kąt prosty, nazywamy trapezem prostokątnym.

Pole kwadratu obliczamy ze wzoru P = a², gdzie 'a' to długość boku. Pole prostokąta to P = a * b, gdzie 'a' i 'b' to długości sąsiednich boków. Pole równoległoboku to P = a * h, gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę. Pole rombu można obliczyć jako P = (d1 * d2) / 2, gdzie d1 i d2 to długości przekątnych, lub jako P = a * h, gdzie 'a' to długość boku, a 'h' to wysokość opuszczona na ten bok. Pole trapezu to P = ((a + b) * h) / 2, gdzie 'a' i 'b' to długości podstaw, a 'h' to wysokość.

Okrąg i Koło

Okrąg to zbiór punktów równoodległych od danego punktu, zwanego środkiem okręgu. Odległość ta nazywana jest promieniem okręgu (r). Koło to zbiór punktów, których odległość od środka jest mniejsza lub równa promieniowi.

Ważne pojęcia związane z okręgiem i kołem to:

Średnica – odcinek łączący dwa punkty na okręgu i przechodzący przez jego środek. Długość średnicy jest dwa razy większa niż długość promienia (d = 2r).
Cięciwa – odcinek łączący dwa punkty na okręgu.
Łuk okręgu – część okręgu ograniczona dwoma punktami.
Wycinek koła – część koła ograniczona dwoma promieniami i łukiem okręgu.
Odcinek koła – część koła ograniczona cięciwą i łukiem okręgu.

Obwód okręgu (czyli długość okręgu) obliczamy ze wzoru: O = 2 * π * r, gdzie π (pi) to liczba niewymierna w przybliżeniu równa 3,14. Pole koła obliczamy ze wzoru: P = π * r².

Symetria

Symetria to ważna cecha figur geometrycznych. Mówimy, że figura jest symetryczna względem prostej (osi symetrii), jeśli po odbiciu lustrzanym względem tej prostej otrzymujemy tę samą figurę. Niektóre figury mają wiele osi symetrii (np. kwadrat ma 4 osie symetrii), inne mają jedną oś symetrii (np. trójkąt równoramienny), a jeszcze inne nie mają żadnej (np. trójkąt różnoboczny).

Mówimy, że figura jest symetryczna względem punktu (środka symetrii), jeśli po obrocie o 180 stopni wokół tego punktu otrzymujemy tę samą figurę. Przykłady figur symetrycznych środkowo to: okrąg, równoległobok, romb, prostokąt, kwadrat.

Pamiętajcie, że dokładne zrozumienie definicji i własności figur geometrycznych oraz umiejętność stosowania odpowiednich wzorów to klucz do sukcesu na sprawdzianie. Ćwiczcie rozwiązywanie zadań, analizujcie rysunki i starajcie się zrozumieć, dlaczego dany wzór działa.

Życzę Wam powodzenia na sprawdzianie! Mam nadzieję, że to kompendium wiedzy Wam pomoże. Pamiętajcie o regularnej nauce i systematycznym powtarzaniu materiału. W razie pytań, zawsze możecie się do mnie zgłosić. Powodzenia!