Figury Na Płaszczyźnie Sprawdzian 3 Gimnaznjum

Figury na płaszczyźnie, w kontekście sprawdzianu dla 3 gimnazjum (obecnie 8 klasy szkoły podstawowej), obejmują zrozumienie i zastosowanie wiedzy o różnych kształtach geometrycznych na dwuwymiarowej powierzchni. Kluczowe jest rozpoznawanie, klasyfikowanie i obliczanie cech charakterystycznych tych figur.

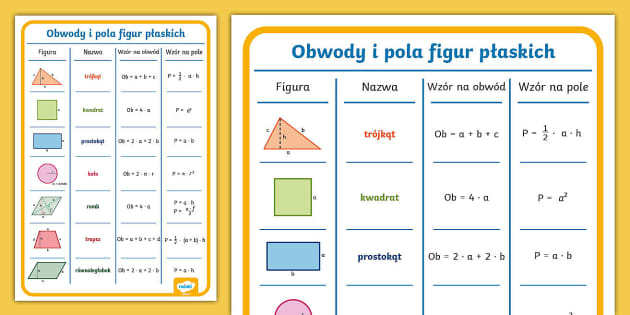
Podstawowe figury to m.in. trójkąty (równoboczny, równoramienny, prostokątny), kwadraty, prostokąty, romby, równoległoboki, trapezy oraz koła i okręgi. Należy znać ich definicje oraz relacje między nimi.

Pole powierzchni i obwód to fundamentalne pojęcia. Uczeń powinien umieć obliczyć pole i obwód każdej z wymienionych figur, znając odpowiednie wzory i wymiary. Na przykład, pole kwadratu o boku 'a' to a², a obwód to 4a. Dla koła, pole to πr², a obwód (długość okręgu) to 2πr, gdzie 'r' to promień.

Twierdzenie Pitagorasa jest szczególnie ważne przy rozwiązywaniu zadań z trójkątami prostokątnymi. a² + b² = c², gdzie 'a' i 'b' to długości przyprostokątnych, a 'c' to długość przeciwprostokątnej.

Podobieństwo figur odnosi się do sytuacji, gdy figury mają identyczny kształt, ale różną wielkość. Stosunek długości odpowiadających sobie boków jest stały. Na przykład, dwa kwadraty o bokach 5 cm i 10 cm są do siebie podobne w skali 1:2.

Symetria jest kolejnym ważnym aspektem. Figury mogą być symetryczne względem punktu (symetria środkowa) lub prostej (symetria osiowa). Rozpoznawanie osi symetrii i środka symetrii jest kluczowe.

Przykład 1: Oblicz pole trójkąta prostokątnego o przyprostokątnych długości 6 cm i 8 cm. Rozwiązanie: Pole = (1/2) * 6 cm * 8 cm = 24 cm².

Przykład 2: Obwód prostokąta wynosi 20 cm. Jeden z boków ma długość 6 cm. Oblicz długość drugiego boku. Rozwiązanie: 2 * (6 cm + b) = 20 cm; b = 4 cm.

Znajomość figur na płaszczyźnie znajduje zastosowanie w wielu dziedzinach życia, od architektury i budownictwa po projektowanie graficzne i kartografię. Umożliwia precyzyjne pomiary, planowanie przestrzenne i rozwiązywanie problemów praktycznych.