Figury Na Plaszczyznie Klasa 8

Witamy w przewodniku po figurach na płaszczyźnie dla uczniów klasy 8! Ten artykuł ma na celu uporządkowanie i wyjaśnienie najważniejszych pojęć geometrycznych, z którymi spotkasz się w tym roku. Geometria to fascynująca dziedzina matematyki, która opisuje kształty, rozmiary, i relacje między obiektami. Zrozumienie tych zagadnień jest kluczowe nie tylko do rozwiązywania zadań na lekcjach, ale również do obserwacji i interpretacji świata wokół nas.

Podstawowe figury i ich właściwości

Zaczniemy od przypomnienia sobie podstawowych figur geometrycznych i ich charakterystycznych cech. To fundament, na którym będziemy budować dalszą wiedzę.

Punkt i prosta

Punkt jest najprostszym obiektem geometrycznym – nie ma wymiarów, tylko położenie. Oznaczamy go zazwyczaj dużą literą alfabetu, np. A, B, C. Prosta to nieskończenie długa linia, która jest idealnie prosta i ma tylko jeden wymiar - długość. Przez dwa punkty można poprowadzić tylko jedną prostą. Odcinek to część prostej ograniczona dwoma punktami, zwanymi końcami odcinka.

Ważne jest, aby odróżniać prostą od półprostej. Półprosta ma początek, ale nie ma końca – rozciąga się w nieskończoność w jednym kierunku.

Kąty

Kąt to figura geometryczna utworzona przez dwie półproste wychodzące z jednego punktu, zwanego wierzchołkiem. Miarę kąta wyrażamy w stopniach (°).

Rozróżniamy następujące rodzaje kątów:

Kąt ostry – jego miara jest mniejsza niż 90°.
Kąt prosty – jego miara wynosi dokładnie 90°.
Kąt rozwarty – jego miara jest większa niż 90°, ale mniejsza niż 180°.
Kąt półpełny – jego miara wynosi dokładnie 180°.
Kąt pełny – jego miara wynosi dokładnie 360°.

Kąty przyległe to dwa kąty, które mają wspólny wierzchołek, jedno ramię wspólne, a pozostałe ramiona tworzą prostą. Suma miar kątów przyległych wynosi 180°. Kąty wierzchołkowe to dwa kąty, które mają wspólny wierzchołek, a ramiona jednego kąta są przedłużeniami ramion drugiego kąta. Kąty wierzchołkowe mają równe miary.

Wielokąty

Wielokąt to figura płaska ograniczona łamaną zamkniętą. Najprostszym wielokątem jest trójkąt. Wielokąty nazwane są od liczby boków (trójkąt – 3 boki, czworokąt – 4 boki, pięciokąt – 5 boków itd.).

Wielokąt foremny to wielokąt, który ma wszystkie boki równej długości i wszystkie kąty równej miary. Przykładami wielokątów foremnych są kwadrat i trójkąt równoboczny.

Trójkąty

Trójkąt to wielokąt o trzech bokach i trzech kątach. Suma miar kątów w trójkącie wynosi zawsze 180°.

Trójkąty dzielimy ze względu na długości boków:

Trójkąt równoboczny – ma wszystkie boki równej długości i wszystkie kąty równe (po 60°).
Trójkąt równoramienny – ma dwa boki równej długości (zwane ramionami) i dwa kąty przy podstawie równe.
Trójkąt różnoboczny – ma wszystkie boki różnej długości i wszystkie kąty różne.

Trójkąty dzielimy również ze względu na miary kątów:

Trójkąt ostrokątny – ma wszystkie kąty ostre (mniejsze niż 90°).
Trójkąt prostokątny – ma jeden kąt prosty (równy 90°). Bok leżący naprzeciw kąta prostego nazywa się przeciwprostokątną, a pozostałe dwa boki to przyprostokątne.
Trójkąt rozwartokątny – ma jeden kąt rozwarty (większy niż 90°).

Twierdzenie Pitagorasa: W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Możemy to zapisać jako: a² + b² = c², gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej. To jedno z najważniejszych twierdzeń w geometrii i ma szerokie zastosowanie.

Wysokość trójkąta to odcinek poprowadzony z wierzchołka trójkąta prostopadle do przeciwległego boku (lub jego przedłużenia). Każdy trójkąt ma trzy wysokości, które przecinają się w jednym punkcie, zwanym ortocentrum.

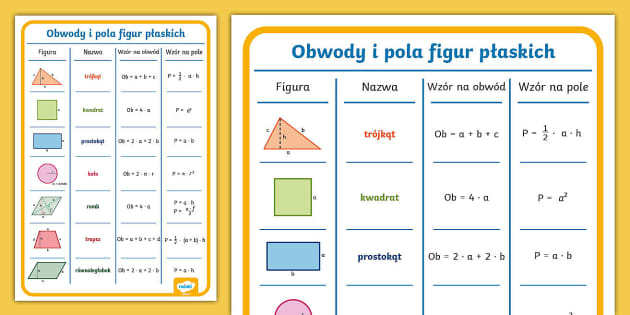
Pole trójkąta można obliczyć na kilka sposobów, np.:

P = (1/2) * a * h, gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę.
Ze wzoru Herona: P = √[s(s-a)(s-b)(s-c)], gdzie a, b, c to długości boków trójkąta, a s to połowa obwodu (s = (a+b+c)/2).

Czworokąty

Czworokąt to wielokąt o czterech bokach i czterech kątach. Suma miar kątów w czworokącie wynosi 360°.

Do najważniejszych rodzajów czworokątów należą:

Równoległobok – ma dwie pary boków równoległych. Przeciwległe boki są równej długości, a przeciwległe kąty są równe. Przekątne równoległoboku przecinają się w połowie.
Prostokąt – to równoległobok, który ma wszystkie kąty proste. Przekątne prostokąta są równej długości.
Romb – to równoległobok, który ma wszystkie boki równej długości. Przekątne rombu przecinają się pod kątem prostym i dzielą kąty wewnętrzne na połowy.
Kwadrat – to prostokąt, który ma wszystkie boki równej długości (lub romb, który ma wszystkie kąty proste). Kwadrat łączy cechy prostokąta i rombu.
Trapez – ma co najmniej jedną parę boków równoległych (zwanych podstawami). Pozostałe dwa boki (zwane ramionami) nie muszą być równoległe.

Trapez równoramienny - ma ramiona równej długości. Kąty przy każdej podstawie są równe.
Trapez prostokątny - ma co najmniej jeden kąt prosty.

Deltoid - ma dwie pary sąsiednich boków równej długości. Przekątne deltoidu przecinają się pod kątem prostym, a jedna z przekątnych dzieli drugą na połowy.

Pole równoległoboku można obliczyć jako: P = a * h, gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę.

Pole prostokąta: P = a * b, gdzie a i b to długości boków prostokąta.

Pole rombu: P = (1/2) * d1 * d2, gdzie d1 i d2 to długości przekątnych rombu.

Pole kwadratu: P = a², gdzie a to długość boku kwadratu.

Pole trapezu: P = (1/2) * (a + b) * h, gdzie a i b to długości podstaw, a h to wysokość trapezu.

Okrąg i koło

Okrąg to zbiór wszystkich punktów na płaszczyźnie, które są oddalone o daną odległość (promień) od danego punktu (środka okręgu). Koło to zbiór wszystkich punktów na płaszczyźnie, których odległość od danego punktu (środka koła) jest mniejsza lub równa danej odległości (promieniowi).

Promień (r) to odcinek łączący środek okręgu z dowolnym punktem na okręgu.

Średnica (d) to odcinek przechodzący przez środek okręgu i łączący dwa punkty na okręgu. Długość średnicy jest dwa razy większa od długości promienia: d = 2r.

Cięciwa to odcinek łączący dwa dowolne punkty na okręgu.

Łuk okręgu to część okręgu ograniczona dwoma punktami.

Wycinek koła to część koła ograniczona dwoma promieniami i łukiem.

Obwód okręgu (długość okręgu): O = 2πr, gdzie π (pi) to liczba niewymierna, w przybliżeniu równa 3,14159.

Pole koła: P = πr².

Przykłady z życia codziennego

Zrozumienie figur geometrycznych ma ogromne znaczenie w wielu dziedzinach życia. Architekci używają geometrii do projektowania budynków i mostów, inżynierowie do projektowania maszyn i urządzeń, graficy komputerowi do tworzenia animacji i gier, a rolnicy do planowania układu pól uprawnych.

Oto kilka przykładów:

Kwadratowe płytki używane do układania podłóg i ścian.
Okrągłe koła w samochodach i rowerach.
Trójkątne dachy budynków.
Prostokątne ekrany telewizorów i komputerów.
Równoległoboczne znaki drogowe

Badania pokazują, że osoby z dobrze rozwiniętą wyobraźnią przestrzenną są często bardziej kreatywne i skuteczne w rozwiązywaniu problemów.

Podsumowanie i dalsza nauka

Geometria figur na płaszczyźnie to fascynująca dziedzina matematyki, która ma wiele zastosowań w życiu codziennym. Ten artykuł przedstawia podstawowe pojęcia i wzory, które musisz znać w klasie 8. Pamiętaj, że kluczem do sukcesu jest regularne powtarzanie materiału i rozwiązywanie zadań. Ćwiczenia pomogą ci utrwalić wiedzę i zrozumieć zależności między różnymi figurami geometrycznymi.

Zachęcamy do dalszego zgłębiania wiedzy z zakresu geometrii. Skorzystaj z podręczników, ćwiczeń, stron internetowych i filmów edukacyjnych. Nie bój się zadawać pytań nauczycielowi i kolegom z klasy. Im więcej będziesz ćwiczyć, tym lepiej zrozumiesz geometrię i tym łatwiej będzie ci rozwiązywać zadania. Powodzenia!