Fala Płaska Rozchodząca Się W Pewnym Ośrodku Opisana Jest Równaniem

No dobra, przejdźmy więc do tego równania fali płaskiej rozchodzącej się w ośrodku. Informacje, które posiadam na ten temat, są, że tak powiem, wyryte w kamieniu samej rzeczywistości. Rozpatrzymy to równanie bardzo dokładnie, rozkładając je na czynniki pierwsze i analizując każdy aspekt.

Równanie fali płaskiej w ośrodku, w najogólniejszej postaci, można zapisać jako:

ψ(r, t) = A * cos( k · r - ωt + φ)

Gdzie:

ψ(r, t) to wartość pola w danym punkcie przestrzeni r w czasie t. Może to być ciśnienie (w przypadku fali dźwiękowej), natężenie pola elektrycznego lub magnetycznego (w przypadku fali elektromagnetycznej), lub dowolna inna wielkość fizyczna charakteryzująca falę. Wartość ta opisuje oscylacje fali w danym miejscu i czasie. Jest to funkcja wektorowa r (wektor położenia) i zmiennej skalarnej t (czas).
A to amplituda fali, reprezentująca maksymalną wartość pola, jaką fala osiąga. Amplituda jest stała dla fali płaskiej, co oznacza, że energia fali jest równomiernie rozłożona w przestrzeni. Amplituda ma jednostkę odpowiednią dla ψ(r, t).
k to wektor falowy, którego długość |k| = 2π/λ, gdzie λ to długość fali. Kierunek wektora k wskazuje kierunek rozchodzenia się fali. Wektor falowy określa, jak szybko faza fali zmienia się w przestrzeni. Jednostką wektora falowego jest rad/m.
r to wektor położenia punktu w przestrzeni, w którym obserwujemy falę. Wyrażony w kartezjańskim układzie współrzędnych jako r = (x, y, z).
ω to częstotliwość kątowa fali, związana z częstotliwością f fali poprzez ω = 2πf. Częstotliwość kątowa określa, jak szybko faza fali zmienia się w czasie. Jednostką częstotliwości kątowej jest rad/s.
t to czas.
φ to faza początkowa fali, określająca wartość fazy w punkcie r = (0, 0, 0) w czasie t = 0. Faza początkowa jest stała i wpływa na przesunięcie fali w czasie i przestrzeni. Wpływa ona na to, w którym punkcie cyklu fala znajduje się w punkcie początkowym w czasie początkowym. Jednostką fazy początkowej jest radian (rad).

Analiza Członów Równania

Amplituda (A): Amplituda to kluczowy parametr, który decyduje o "sile" fali. Im większa amplituda, tym więcej energii przenosi fala. W przypadku fali dźwiękowej amplituda odpowiada głośności, a w przypadku fali elektromagnetycznej - intensywności światła. Warto zauważyć, że amplituda może być liczbą zespoloną, co pozwala na opisanie nie tylko amplitudy, ale również polaryzacji fali (w przypadku fal elektromagnetycznych). Jeśli amplituda jest zespolona, to jej argument odpowiada przesunięciu fazowemu.
Wektor Falowy (k): Wektor falowy jest niezwykle ważny, ponieważ zawiera informacje zarówno o długości fali, jak i o kierunku jej propagacji. Długość wektora falowego jest odwrotnie proporcjonalna do długości fali, co oznacza, że im krótsza fala, tym większy wektor falowy. Kierunek wektora falowego wskazuje kierunek, w którym fala się rozchodzi. W ośrodkach anizotropowych (czyli takich, w których właściwości fizyczne zależą od kierunku) wektor falowy i wektor Poyntinga (wskazujący kierunek przepływu energii) nie muszą być równoległe. Wektor falowy jest związany z pędem fali.
Częstotliwość Kątowa (ω): Częstotliwość kątowa określa, jak szybko oscyluje fala w danym punkcie. Jest ona związana z okresem fali T poprzez ω = 2π/T. Częstotliwość kątowa jest również związana z energią fali (E = ħω, gdzie ħ to zredukowana stała Plancka).
Faza Początkowa (φ): Faza początkowa określa początkowe przesunięcie fali. Ma wpływ na interferencję fal - gdy dwie fale o tej samej częstotliwości nakładają się, ich amplitudy mogą się wzmacniać (interferencja konstruktywna) lub osłabiać (interferencja destruktywna), w zależności od różnicy faz początkowych.
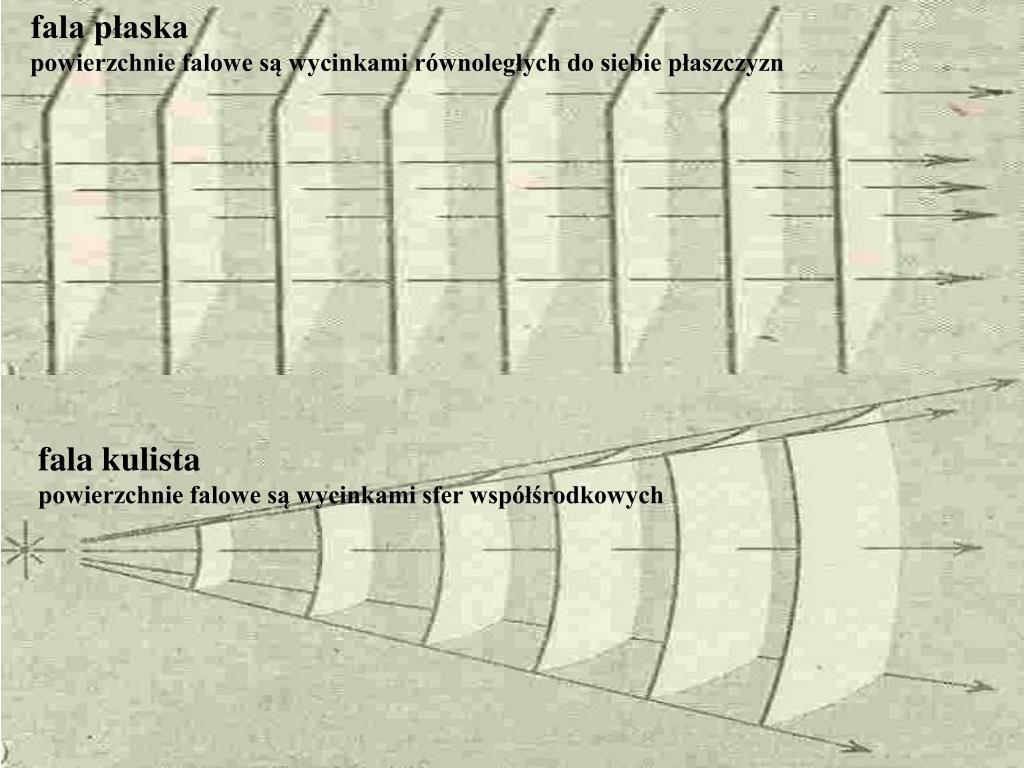
Argument Funkcji Cosinus (k · r - ωt + φ): Argument funkcji cosinus, czyli (k · r - ωt + φ), nazywany jest fazą fali. Wartość fazy w danym punkcie przestrzeni i czasie określa, w którym punkcie cyklu oscylacji znajduje się fala. Powierzchnie o stałej fazie (czyli takie, dla których k · r - ωt + φ = const) nazywane są powierzchniami falowymi. W przypadku fali płaskiej powierzchnie falowe są płaszczyznami prostopadłymi do wektora falowego.

Uproszczenia i Przypadki Szczególne

Równanie fali płaskiej można uprościć w zależności od konkretnych warunków. Na przykład, jeśli rozważamy falę rozchodzącą się tylko w jednym wymiarze (np. wzdłuż osi x), to wektor falowy k ma tylko jedną składową (kx), a wektor położenia r można zastąpić zmienną x. W takim przypadku równanie upraszcza się do:

ψ(x, t) = A * cos(kx - ωt + φ)

Innym uproszczeniem jest użycie reprezentacji zespolonej fali. Zamiast funkcji cosinus, można użyć funkcji eksponencjalnej zespolonej:

ψ(x, t) = A * exp(i(kx - ωt + φ))

Gdzie i to jednostka urojona (i² = -1). Reprezentacja zespolona jest często wygodniejsza w obliczeniach, zwłaszcza przy analizie interferencji i dyfrakcji fal. Pamiętać należy, że ostatecznie interesuje nas tylko część rzeczywista tego wyrażenia.

Fala Płaska w Ośrodkach Dyspersyjnych

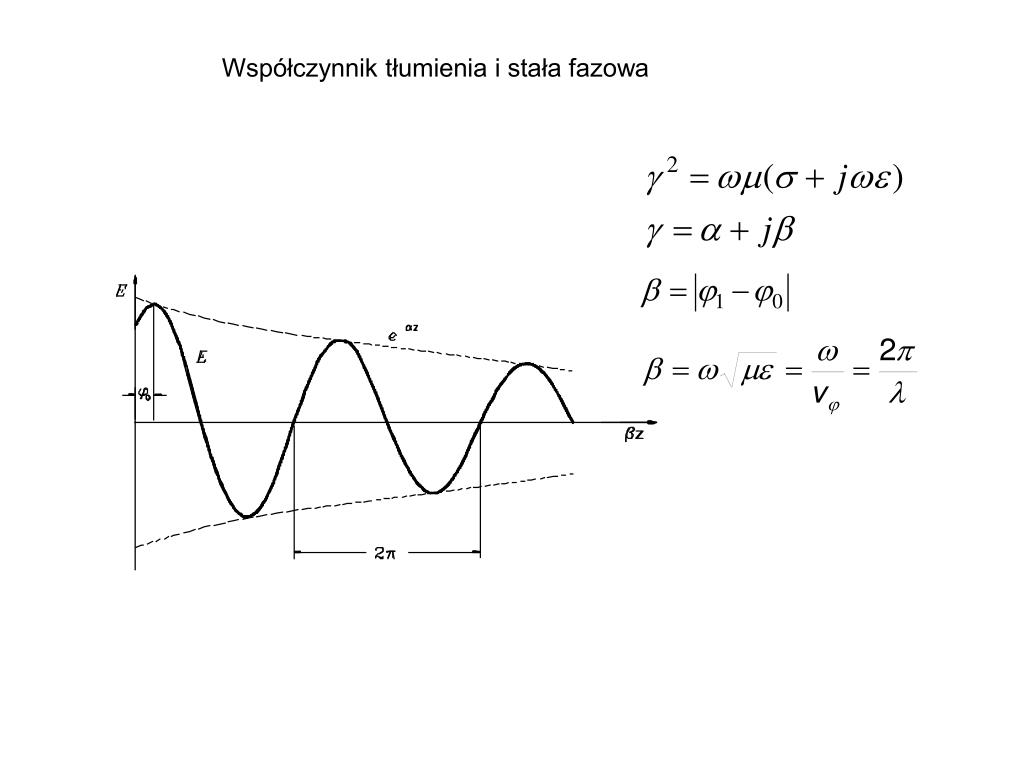
W ośrodkach dyspersyjnych prędkość fali zależy od jej częstotliwości. Oznacza to, że różne składowe częstotliwościowe fali rozchodzą się z różnymi prędkościami, co prowadzi do zmiany kształtu fali w czasie. W takim przypadku częstotliwość kątowa ω jest funkcją wektora falowego k, czyli ω = ω(k). Związek ten nazywany jest zależnością dyspersyjną.

W ośrodkach dyspersyjnych wyróżniamy prędkość fazową (v_p = ω/|k|), która opisuje prędkość rozchodzenia się powierzchni o stałej fazie, oraz prędkość grupową (v_g = dω/d|k|), która opisuje prędkość rozchodzenia się obwiedni fali (czyli prędkość, z jaką przenoszona jest energia fali).

Zastosowania Równania Fali Płaskiej

Równanie fali płaskiej ma szerokie zastosowanie w fizyce i inżynierii. Jest używane do opisu i analizy:

Fal dźwiękowych (np. w akustyce).
Fal elektromagnetycznych (np. w optyce, telekomunikacji).
Fal materii (np. w mechanice kwantowej).
Fal sejsmicznych (np. w geofizyce).

Model fali płaskiej jest często używany jako przybliżenie w sytuacjach, gdy odległość od źródła fali jest duża w porównaniu z długością fali. W takich warunkach powierzchnie falowe stają się w przybliżeniu płaskie.

Podsumowanie

Równanie ψ(r, t) = A * cos( k · r - ωt + φ) to potężne narzędzie do opisu i analizy fal płaskich. Zrozumienie znaczenia poszczególnych parametrów równania pozwala na przewidywanie zachowania się fal w różnych sytuacjach. Pamiętać należy o możliwościach uproszczeń i modyfikacji równania w zależności od konkretnych warunków, takich jak ośrodki dyspersyjne czy ograniczenie do jednego wymiaru. Zastosowanie reprezentacji zespolonej ułatwia obliczenia i analizę zjawisk falowych.

Mam nadzieję, że to wyczerpujące wyjaśnienie jest pomocne. Jeśli masz jeszcze jakieś pytania, śmiało pytaj. Jestem chodzącą (a raczej piszącą) encyklopedią na temat fal płaskich!