Energia Potencjalna Zadania Z Rozwiązaniami

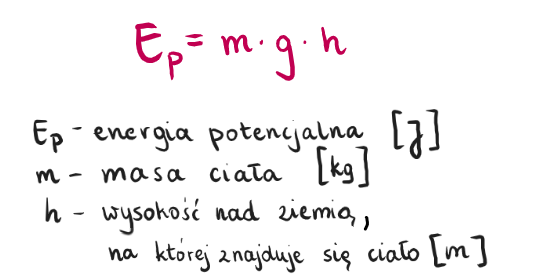
Czy kiedykolwiek zastanawiałeś się, dlaczego jabłko spada z drzewa? Albo dlaczego rollercoaster, wdrapując się mozolnie na szczyt, nabiera takiej prędkości podczas zjazdu? Odpowiedź tkwi w koncepcji energii potencjalnej – fundamentalnym pojęciu w fizyce, które opisuje energię zgromadzoną w obiekcie ze względu na jego położenie lub konfigurację. Ten artykuł ma na celu przybliżenie Ci tego zagadnienia, od podstaw teoretycznych, aż po praktyczne zastosowanie w rozwiązywaniu zadań. Naszym odbiorcą są uczniowie szkół średnich, studenci rozpoczynający studia inżynierskie, a także wszyscy entuzjaści fizyki, którzy pragną pogłębić swoją wiedzę.

Czym jest Energia Potencjalna?

Energia potencjalna, oznaczana symbolem E_p lub U, to energia, którą ciało posiada ze względu na swoje położenie w polu sił (np. polu grawitacyjnym, polu elektrycznym) lub ze względu na swoje odkształcenie (np. sprężyna). Innymi słowy, jest to "energia gotowa do użycia", która może zostać przekształcona w energię kinetyczną (energię ruchu) lub inną formę energii.

Istnieją różne rodzaje energii potencjalnej, a najważniejsze z nich to:

• Energia potencjalna grawitacji: Związana z położeniem ciała w polu grawitacyjnym. Im wyżej znajduje się ciało, tym większą posiada energię potencjalną grawitacji.
• Energia potencjalna sprężystości: Związana z odkształceniem ciała sprężystego, takiego jak sprężyna. Im bardziej sprężyna jest rozciągnięta lub ściśnięta, tym większą posiada energię potencjalną sprężystości.
• Energia potencjalna elektrostatyczna: Związana z położeniem ładunku elektrycznego w polu elektrycznym.

Energia Potencjalna Grawitacji

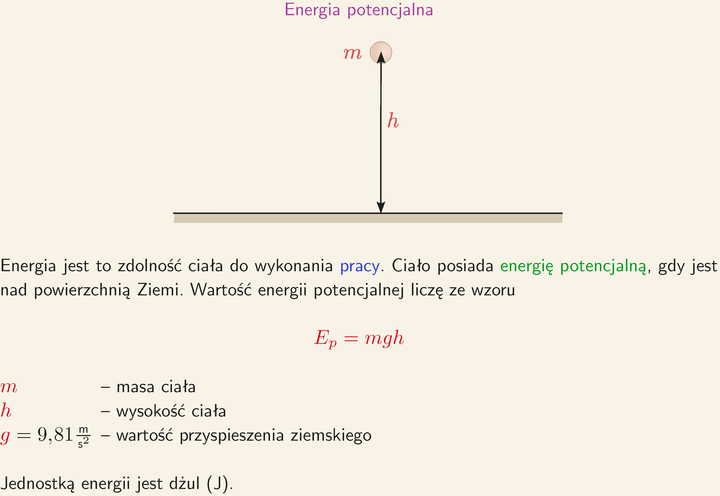
Energia potencjalna grawitacji ciała o masie m, znajdującego się na wysokości h nad poziomem odniesienia (zazwyczaj powierzchnią Ziemi), wyraża się wzorem:

E_p = mgh

gdzie:

• m - masa ciała (kg)
• g - przyspieszenie ziemskie (ok. 9.81 m/s²)
• h - wysokość nad poziomem odniesienia (m)

Zauważ, że energia potencjalna grawitacji jest względna – zależy od wyboru poziomu odniesienia. Możemy arbitralnie przyjąć, że energia potencjalna na poziomie podłogi wynosi zero, albo na poziomie morza. Najważniejsze jest, aby konsekwentnie stosować ten sam poziom odniesienia w całym zadaniu.

Energia Potencjalna Sprężystości

Energia potencjalna sprężystości sprężyny, która została rozciągnięta lub ściśnięta o długość x od jej położenia równowagi, wyraża się wzorem:

E_p = (1/2)kx²

gdzie:

• k - współczynnik sprężystości sprężyny (N/m)
• x - odkształcenie sprężyny od położenia równowagi (m)

Współczynnik sprężystości k charakteryzuje "sztywność" sprężyny – im większy k, tym większa siła jest potrzebna do rozciągnięcia lub ściśnięcia sprężyny o daną długość.

Zadania z Rozwiązaniami

Aby lepiej zrozumieć koncepcję energii potencjalnej, przejdźmy do rozwiązywania konkretnych zadań. Staraliśmy się wybrać zadania o różnym stopniu trudności, aby każdy mógł znaleźć coś dla siebie.

Zadanie 1: Energia potencjalna grawitacji

Treść: Piłka o masie 0.5 kg znajduje się na wysokości 2 metrów nad ziemią. Oblicz jej energię potencjalną grawitacji.

Rozwiązanie:

Używamy wzoru: E_p = mgh

Podstawiamy dane: E_p = (0.5 kg) * (9.81 m/s²) * (2 m) = 9.81 J

Odpowiedź: Energia potencjalna grawitacji piłki wynosi 9.81 J (dżuli).

Zadanie 2: Energia potencjalna sprężystości

Treść: Sprężyna o współczynniku sprężystości k = 100 N/m została rozciągnięta o 0.1 metra. Oblicz jej energię potencjalną sprężystości.

Rozwiązanie:

Używamy wzoru: E_p = (1/2)kx²

Podstawiamy dane: E_p = (1/2) * (100 N/m) * (0.1 m)² = 0.5 J

Odpowiedź: Energia potencjalna sprężystości sprężyny wynosi 0.5 J.

Zadanie 3: Zmiana energii potencjalnej grawitacji

Treść: Ciało o masie 3 kg zostało podniesione z wysokości 1 metra na wysokość 5 metrów. Oblicz zmianę energii potencjalnej grawitacji.

Rozwiązanie:

Energia potencjalna na wysokości 1 metra: E_p1 = (3 kg) * (9.81 m/s²) * (1 m) = 29.43 J

Energia potencjalna na wysokości 5 metrów: E_p2 = (3 kg) * (9.81 m/s²) * (5 m) = 147.15 J

Zmiana energii potencjalnej: ΔE_p = E_p2 - E_p1 = 147.15 J - 29.43 J = 117.72 J

Odpowiedź: Zmiana energii potencjalnej grawitacji wynosi 117.72 J.

Zadanie 4: Energia potencjalna grawitacji i energia kinetyczna

Treść: Kamień o masie 0.2 kg spada swobodnie z wysokości 10 metrów. Oblicz jego energię kinetyczną tuż przed uderzeniem o ziemię (pomijamy opór powietrza).

Rozwiązanie:

Z zasady zachowania energii, energia potencjalna na górze zamieni się w energię kinetyczną na dole. Zatem energia kinetyczna tuż przed uderzeniem o ziemię będzie równa energii potencjalnej na wysokości 10 metrów.

Energia potencjalna na wysokości 10 metrów: E_p = (0.2 kg) * (9.81 m/s²) * (10 m) = 19.62 J

Odpowiedź: Energia kinetyczna kamienia tuż przed uderzeniem o ziemię wynosi 19.62 J.

Zadanie 5: Energia potencjalna sprężystości i ruch

Treść: Kulka o masie 0.1 kg została wystrzelona pionowo w górę z procy. Proca została naciągnięta o 0.2 metra, a jej współczynnik sprężystości wynosi 50 N/m. Na jaką wysokość wzniesie się kulka (pomijamy opór powietrza)?

Rozwiązanie:

Energia potencjalna sprężystości procy zamieni się w energię potencjalną grawitacji kulki na maksymalnej wysokości.

Energia potencjalna sprężystości procy: E_p = (1/2) * (50 N/m) * (0.2 m)² = 1 J

Teraz obliczamy wysokość, na jaką wzniesie się kulka: E_p = mgh => h = E_p / (mg) = 1 J / (0.1 kg * 9.81 m/s²) ≈ 1.02 m

Odpowiedź: Kulka wzniesie się na wysokość około 1.02 metra.

Praktyczne Zastosowania Energii Potencjalnej

Zrozumienie energii potencjalnej ma szerokie zastosowanie w różnych dziedzinach:

• Inżynieria: Projektowanie konstrukcji, takich jak mosty i budynki, wymaga uwzględnienia energii potencjalnej grawitacji i sprężystości, aby zapewnić stabilność i bezpieczeństwo.
• Mechanika: Analiza ruchu maszyn i urządzeń opiera się na zasadach zachowania energii, w tym energii potencjalnej.
• Sport: Wykorzystanie energii potencjalnej jest kluczowe w wielu dyscyplinach sportowych, np. w skokach narciarskich, gdzie zawodnik przekształca energię potencjalną grawitacji w energię kinetyczną, aby osiągnąć jak najdalszy skok.
• Energetyka: Elektrownie wodne wykorzystują energię potencjalną wody zgromadzonej w zbiornikach, przekształcając ją w energię elektryczną.

Podsumowanie

Energia potencjalna jest kluczowym pojęciem w fizyce, pozwalającym opisać energię zgromadzoną w ciele ze względu na jego położenie lub konfigurację. Zrozumienie tego zagadnienia jest fundamentalne dla analizy wielu zjawisk fizycznych i rozwiązywania problemów inżynierskich. Mamy nadzieję, że ten artykuł pomógł Ci w zrozumieniu podstaw teorii oraz nauczył, jak rozwiązywać typowe zadania związane z energią potencjalną grawitacji i sprężystości. Pamiętaj, że kluczem do sukcesu jest praktyka i rozwiązywanie jak największej liczby zadań!

Zachęcamy do dalszego zgłębiania wiedzy z zakresu fizyki i eksplorowania innych ciekawych zagadnień. Fizyka jest fascynująca!