Energia Potencjalna Wzór

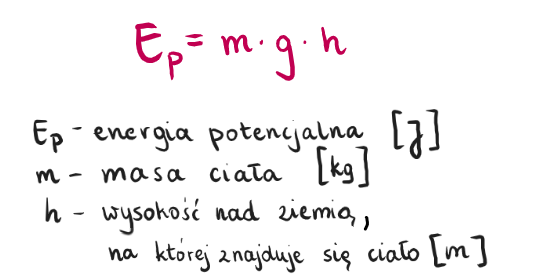
Czy kiedykolwiek zastanawiałeś się, dlaczego wspinaczka górska jest tak wyczerpująca, a jazda na rollercoasterze tak ekscytująca? Często, nie zdajemy sobie sprawy z tego, że za tymi zjawiskami kryje się jedno z fundamentalnych pojęć fizyki – energia potencjalna.

Wydaje się skomplikowane? Nie musi! W tym artykule rozłożymy wzór na energię potencjalną na czynniki pierwsze, pokazując, jak go zrozumieć i wykorzystać w praktyce. Bez zbędnego żargonu, skupimy się na tym, co najważniejsze, abyś mógł/mogła poczuć się pewnie w temacie fizyki.

Czym jest energia potencjalna? Proste wyjaśnienie.

Energia potencjalna, w najprostszym ujęciu, to energia "ukryta" w obiekcie ze względu na jego pozycję lub stan. Wyobraź sobie piłkę na szczycie wzgórza. Nie porusza się, ale ma potencjał do ruchu. Ten potencjał, wynikający z jej wysokości, to właśnie energia potencjalna.

Można powiedzieć, że to energia "oczekiwania". Czeka, aż warunki się zmienią, a ona zamieni się w energię kinetyczną – energię ruchu.

Istnieją różne rodzaje energii potencjalnej, ale dwa najpopularniejsze to:

Energia potencjalna grawitacji: Związana z wysokością obiektu nad powierzchnią Ziemi.
Energia potencjalna sprężystości: Związana z odkształceniem sprężystego ciała, na przykład naciągniętej gumki lub ściśniętej sprężyny.

Dziś skupimy się głównie na energii potencjalnej grawitacji, ponieważ jest ona najczęściej spotykana i najłatwiejsza do zrozumienia.

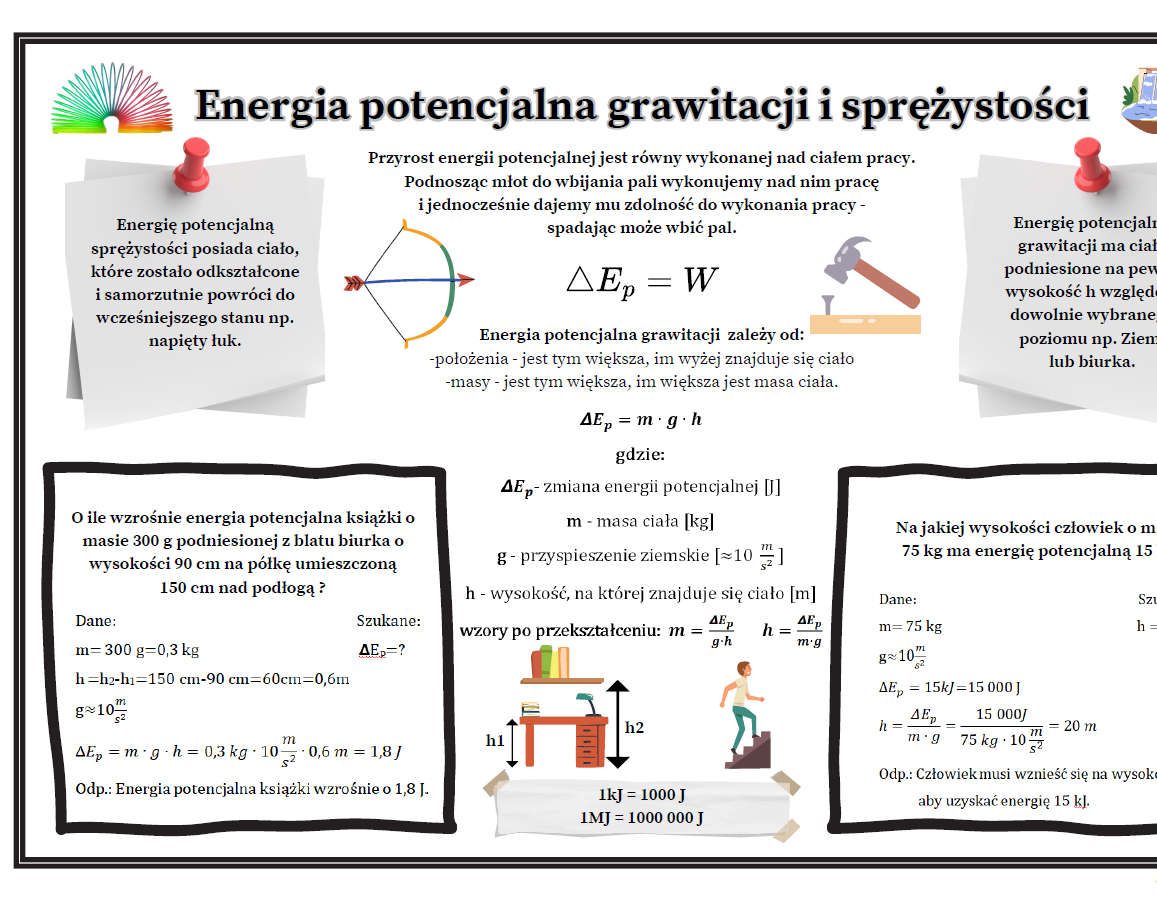
Wzór na energię potencjalną grawitacji - rozkładamy na czynniki

Wzór na energię potencjalną grawitacji wygląda następująco:

E_p = m * g * h

Gdzie:

E_p to energia potencjalna (mierzona w dżulach - J).
m to masa obiektu (mierzona w kilogramach - kg).
g to przyspieszenie ziemskie (w przybliżeniu 9.81 m/s²). To stała wartość, reprezentująca siłę, z jaką Ziemia przyciąga obiekty.
h to wysokość obiektu nad punktem odniesienia (mierzona w metrach - m). Punkt odniesienia wybieramy sami - zazwyczaj jest to podłoga, grunt lub poziom morza.

Spójrzmy na to na przykładzie. Wyobraź sobie, że trzymasz w ręce piłkę o masie 0.5 kg na wysokości 2 metrów nad ziemią. Jej energia potencjalna wynosi:

E_p = 0.5 kg * 9.81 m/s² * 2 m = 9.81 J

Oznacza to, że piłka ma 9.81 dżuli energii potencjalnej z powodu swojej wysokości.

Jak interpretować wyniki?

Im większa masa obiektu i im wyżej się znajduje, tym większa jest jego energia potencjalna. To intuicyjne – cięższy przedmiot upuszczony z większej wysokości wyrządzi więcej szkód, ponieważ ma więcej energii do uwolnienia.

Warto zauważyć, że energia potencjalna jest względna. Zależy od wybranego punktu odniesienia. Jeśli za punkt odniesienia przyjęlibyśmy wysokość 2 metrów, to energia potencjalna piłki byłaby równa zeru.

Przykłady z życia codziennego

Energia potencjalna grawitacji otacza nas każdego dnia, choć często tego nie zauważamy. Oto kilka przykładów:

Woda w jeziorze górskim: Jezioro położone wysoko w górach ma dużą energię potencjalną. Gdy woda spływa w dół rzeką, energia potencjalna zamienia się w energię kinetyczną, napędzając turbiny w elektrowniach wodnych.
Rollercoaster: Wagonik rollercoastera, wjeżdżając na szczyt wzniesienia, gromadzi energię potencjalną. Gdy zaczyna zjeżdżać w dół, ta energia zamienia się w energię kinetyczną, dając nam zastrzyk adrenaliny.
Jabłko na drzewie: Jabłko wiszące na gałęzi drzewa ma energię potencjalną. Gdy spadnie, ta energia zamienia się w energię kinetyczną, a następnie w energię uderzenia o ziemię.
Podnoszenie ciężarów: Podczas podnoszenia ciężaru, pracujemy nad zwiększeniem jego energii potencjalnej. Im wyżej podniesiemy ciężar, tym więcej energii potencjalnej w nim zgromadzimy.

Energia potencjalna sprężystości - krótko o innym rodzaju

Jak już wspomnieliśmy, istnieje również energia potencjalna sprężystości. Dotyczy ona ciał, które mogą się odkształcać i powracać do swojego pierwotnego kształtu, takich jak sprężyny, gumki, czy łuki.

Wzór na energię potencjalną sprężystości wygląda następująco:

E_p = (1/2) * k * x²

Gdzie:

E_p to energia potencjalna sprężystości (mierzona w dżulach - J).
k to współczynnik sprężystości (charakteryzuje sztywność sprężyny – im większy współczynnik, tym sztywniejsza sprężyna).
x to odkształcenie sprężyny (czyli o ile sprężyna została rozciągnięta lub ściśnięta względem jej pierwotnej długości).

Przykład: Naciągając sprężynę, gromadzimy w niej energię potencjalną sprężystości. Po zwolnieniu sprężyny, energia ta zamienia się w energię kinetyczną, wprawiając w ruch przedmioty związane ze sprężyną.

Praktyczne zastosowania wiedzy o energii potencjalnej

Zrozumienie koncepcji energii potencjalnej ma wiele praktycznych zastosowań:

Inżynieria: Projektowanie budynków, mostów i innych konstrukcji wymaga uwzględnienia energii potencjalnej, aby zapewnić ich stabilność i bezpieczeństwo.
Sport: Sportowcy często wykorzystują energię potencjalną do poprawy swoich wyników. Na przykład, skoczkowie wzwyż zamieniają energię kinetyczną rozbiegu na energię potencjalną w najwyższym punkcie skoku, a następnie znów na energię kinetyczną podczas opadania.
Energetyka: Elektrownie wodne wykorzystują energię potencjalną wody zgromadzonej w zbiornikach, aby wytwarzać energię elektryczną.
Edukacja: Zrozumienie energii potencjalnej jest kluczowe do zrozumienia innych pojęć fizycznych, takich jak energia kinetyczna, praca i moc.

Kilka wskazówek na zakończenie

Oto kilka wskazówek, które pomogą Ci lepiej zrozumieć i wykorzystać wzór na energię potencjalną:

Pamiętaj o jednostkach: Upewnij się, że używasz odpowiednich jednostek (kg dla masy, m dla wysokości, m/s² dla przyspieszenia ziemskiego), aby otrzymać wynik w dżulach.
Wybierz punkt odniesienia: Wybierz odpowiedni punkt odniesienia dla wysokości. Pamiętaj, że energia potencjalna jest względna i zależy od tego wyboru.
Wykorzystuj przykłady: Ćwicz rozwiązywanie zadań z różnymi przykładami, aby lepiej zrozumieć wzór i jego zastosowania.
Nie bój się zadawać pytań: Jeśli masz wątpliwości, nie wahaj się pytać nauczyciela, profesora lub poszukać informacji w wiarygodnych źródłach.

Podsumowanie

Energia potencjalna to fundamentalne pojęcie fizyczne, które opisuje energię "ukrytą" w obiekcie ze względu na jego pozycję lub stan. Zrozumienie wzoru na energię potencjalną grawitacji (E_p = m * g * h) pozwala na lepsze zrozumienie otaczającego nas świata i jego praw. Od wspinaczki górskiej po projektowanie rollercoasterów, energia potencjalna odgrywa ważną rolę w wielu dziedzinach naszego życia. Mam nadzieję, że ten artykuł pomógł Ci zrozumieć to fascynujące pojęcie i zachęcił do dalszego zgłębiania wiedzy o fizyce!