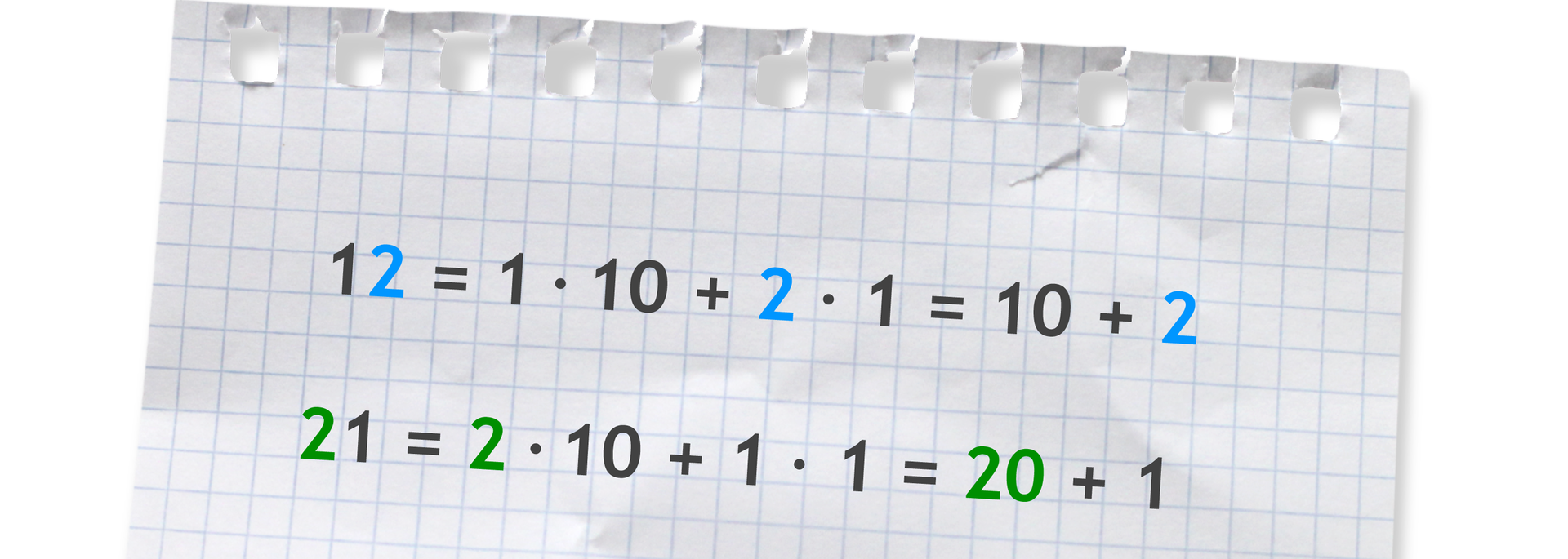Dziesiątkowy System Pozycyjny Klasa 2

Hej! Pamiętacie system dziesiątkowy? Ten, który uczyli nas w drugiej klasie? No właśnie. Mam wrażenie, że nikt nie docenia jego geniuszu.

Lekcja, którą pozornie zapomnieliśmy

Pomyślcie o tym. Mamy tylko 10 cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9. I z ich pomocą możemy policzyć... wszystko! Od ilości ciasteczek w słoiku po gwiazdy na niebie (no, prawie!). To jest niesamowite, serio!

Miejsce ma znaczenie

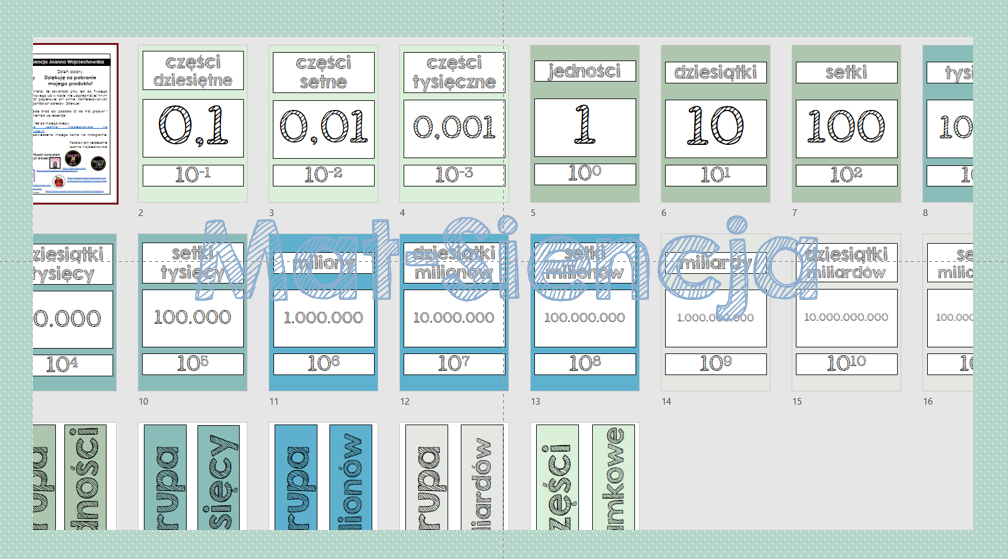
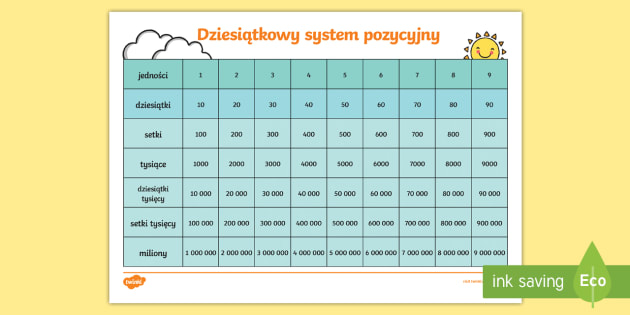
I to, co najważniejsze: pozycja cyfry ma znaczenie! To nie tylko "2", to może być 2 jednostki, 2 dziesiątki (czyli 20!), 2 setki (200!), a nawet 2 miliony! Proste, ale genialne. Inne systemy? Cóż, powiedzmy, że wolę nie myśleć o rzymskich cyfrach...

MCMLXXXIV... aż mi się odechciewa liczyć.

Czy tylko ja uważam, że powinniśmy codziennie rano dziękować matematykom za system dziesiątkowy? Może jakaś krótka modlitwa? "O, potęgo miejsc dziesiętnych, dziękujemy za prostotę i uniwersalność..." No dobra, może trochę przesadzam.

Niekochany geniusz?

Serio, ile razy słyszycie, żeby ktoś ekscytował się systemem dziesiątkowym? Raczej wolicie narzekać na kalkulacje w korporacjach, prawda? Albo na to, że w sklepie oszukują na reszcie. Ale to nie wina systemu! To wina ludzi, którzy go źle używają!

Plusy dodatnie i ujemne

Jasne, czasem wolę liczyć na palcach, ale to tylko dlatego, że lubię tradycję. I żeby poćwiczyć paluszki! Poza tym, system dziesiątkowy pozwala mi obliczyć, ile pieniędzy potrzebuję na kolejną parę butów (dużo!) albo ile dni zostało do wakacji (zbyt dużo!).

Naprawdę uważam, że system dziesiątkowy to niedoceniony bohater naszych czasów. Powinniśmy częściej o nim mówić, pisać wiersze ku jego czci i budować mu pomniki! (Może nie pomniki, ale jakiś mały post na Instagramie by się przydał!).

Więc następnym razem, gdy będziecie liczyć pieniądze, piec ciasto albo planować wakacje, pomyślcie o tym biednym, samotnym systemie dziesiątkowym. On tam jest, cichutko pracuje i sprawia, że nasze życie jest o wiele łatwiejsze. A my go kompletnie ignorujemy!

Czy tylko ja tak mam? No, powiedzcie, że nie jestem sam w tej miłości do pozycyjnego systemu dziesiątkowego! I niech ta miłość trwa wiecznie! (Albo przynajmniej do następnej lekcji matematyki!).