Dzielenie Ułamków Dziesiętnych Klasa 5

Witajcie, młodzi matematycy! Dziś zagłębimy się w fascynujący świat dzielenia ułamków dziesiętnych. Może na początku wydaje się to trudne, ale obiecuję, że krok po kroku wszystko stanie się jasne jak słońce!

Czym jest ułamek dziesiętny?

Zanim zaczniemy dzielić, upewnijmy się, że rozumiemy, czym jest ułamek dziesiętny. Ułamek dziesiętny to po prostu inny sposób zapisywania ułamka zwykłego, który ma w mianowniku 10, 100, 1000 i tak dalej. Na przykład, ułamek ¹/₁₀ możemy zapisać jako 0,1, a ²⁵/₁₀₀ jako 0,25. Liczba po przecinku dziesiętnym reprezentuje właśnie te części dziesiętne, setne, tysięczne itd.

Dzielenie ułamka dziesiętnego przez liczbę naturalną

Zacznijmy od prostszego przypadku: dzielenia ułamka dziesiętnego przez liczbę naturalną (czyli całą liczbę, np. 1, 2, 3, 4...). Jak to zrobić? Najprościej jest potraktować ułamek dziesiętny jak zwykłą liczbę całkowitą, wykonując dzielenie pisemne, a następnie umieścić przecinek dziesiętny w wyniku w odpowiednim miejscu.

Przykład: 6,8 : 2

Wyobraź sobie, że dzielisz 68 przez 2.
Wynik to 34.
Ponieważ w 6,8 mieliśmy jedno miejsce po przecinku, w wyniku również musimy mieć jedno miejsce po przecinku. Zatem 34 zamienia się w 3,4.

Odp: 6,8 : 2 = 3,4

Inny przykład: 12,45 : 5

Wyobraź sobie, że dzielisz 1245 przez 5.
Wynik to 249.
W 12,45 mamy dwa miejsca po przecinku, więc w wyniku również musimy mieć dwa miejsca po przecinku. Zatem 249 zamienia się w 2,49.

Odp: 12,45 : 5 = 2,49

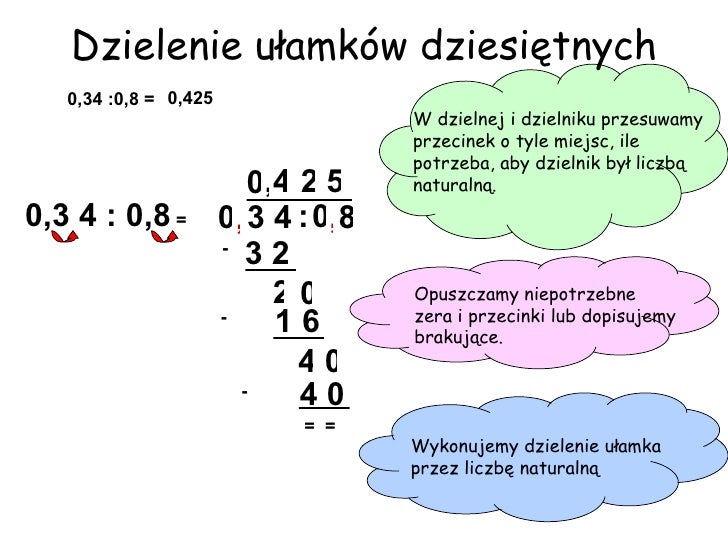
Dzielenie ułamka dziesiętnego przez ułamek dziesiętny – najważniejszy krok!

Teraz przejdźmy do sedna sprawy: dzielenia ułamka dziesiętnego przez inny ułamek dziesiętny. Tutaj potrzebujemy pewnej sztuczki, aby ułatwić sobie życie. Sztuczka polega na przesunięciu przecinka zarówno w dzielnej (liczba, którą dzielimy), jak i w dzielniku (liczba, przez którą dzielimy), tak aby dzielnik stał się liczbą całkowitą.

Przykład: 4,8 : 1,2

Spójrz na dzielnik (1,2). Ile miejsc po przecinku ma dzielnik? W tym przypadku jedno.
Przesuń przecinek w dzielniku o jedno miejsce w prawo. 1,2 staje się 12.
Teraz *musisz* przesunąć przecinek o *tyle samo* miejsc w prawo również w dzielnej (4,8). 4,8 staje się 48.
Teraz zamiast 4,8 : 1,2, mamy 48 : 12. Dużo łatwiej, prawda?
48 : 12 = 4

Odp: 4,8 : 1,2 = 4

Kolejny przykład: 0,36 : 0,09

Spójrz na dzielnik (0,09). Ile miejsc po przecinku ma dzielnik? W tym przypadku dwa.
Przesuń przecinek w dzielniku o dwa miejsca w prawo. 0,09 staje się 9.
Przesuń przecinek o dwa miejsca w prawo również w dzielnej (0,36). 0,36 staje się 36.
Teraz zamiast 0,36 : 0,09, mamy 36 : 9.
36 : 9 = 4

Odp: 0,36 : 0,09 = 4

Przykład z "dopisywaniem zer": 1,5 : 0,25

Spójrz na dzielnik (0,25). Dwa miejsca po przecinku.
Przesuń przecinek w dzielniku o dwa miejsca w prawo. 0,25 staje się 25.
Przesuń przecinek o dwa miejsca w prawo również w dzielnej (1,5). Ale czekaj! Mamy tylko jedno miejsce po przecinku. Co robić?
Dopisujemy zero! 1,5 staje się 1,50 (wartość się nie zmienia!). Teraz możemy przesunąć przecinek o dwa miejsca w prawo i otrzymujemy 150.
Teraz zamiast 1,5 : 0,25, mamy 150 : 25.
150 : 25 = 6

Odp: 1,5 : 0,25 = 6

Dlaczego to działa?

Przesuwanie przecinka to tak naprawdę mnożenie zarówno dzielnej, jak i dzielnika przez 10, 100, 1000 itd. (w zależności od tego, ile miejsc przesuwamy przecinek). Pamiętaj, że jeśli pomnożysz dzielną i dzielnik przez tę samą liczbę, wynik dzielenia się nie zmieni! To tak, jakbyś miał 10 ciasteczek podzielić między 2 osoby (10:2 = 5). Jeśli podwoisz liczbę ciasteczek (20) i podwoisz liczbę osób (4), to każda osoba nadal dostanie 5 ciasteczek (20:4 = 5).

Praktyczne zastosowania

Dzielenie ułamków dziesiętnych przydaje się w wielu sytuacjach w życiu codziennym. Na przykład:

Kupowanie na wagę: Jeśli wiesz, ile kosztuje 1 kg jabłek (np. 4,50 zł) i chcesz kupić 0,7 kg, to aby obliczyć, ile zapłacisz, musisz pomnożyć 4,50 przez 0,7. Ale równie dobrze możesz chcieć podzielić całkowity koszt przez wagę, żeby sprawdzić, czy cena za kilogram się zgadza.
Dzielenie rachunku: Jeśli z przyjaciółmi jesz w restauracji i chcesz podzielić rachunek na równe części, musisz podzielić kwotę rachunku (np. 85,50 zł) przez liczbę osób.
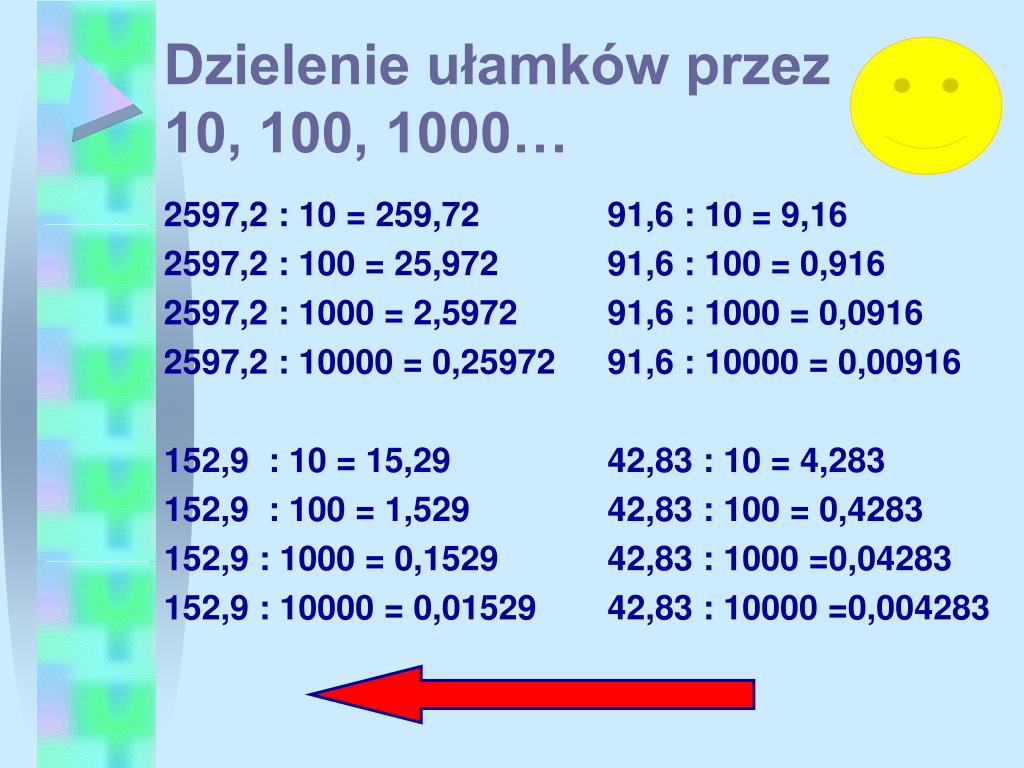
Przeliczanie jednostek: Możesz użyć dzielenia ułamków dziesiętnych do przeliczania jednostek, na przykład centymetrów na metry (dzieląc liczbę centymetrów przez 100).

Podsumowanie

Pamiętaj, że kluczem do sukcesu w dzieleniu ułamków dziesiętnych jest zrozumienie idei przesuwania przecinka. Po opanowaniu tej techniki, zadania staną się o wiele łatwiejsze. Ćwicz, ćwicz i jeszcze raz ćwicz, a wkrótce będziesz mistrzem dzielenia ułamków dziesiętnych! Powodzenia!

„Matematyka jest królową nauk, a arytmetyka królową matematyki.” – Carl Friedrich Gauss

Jeśli masz jakieś pytania, nie wahaj się ich zadać! Pamiętaj, że najważniejsze to zrozumieć zasadę, a potem ćwiczyć, aby nabrać wprawy. Dzielenie ułamków dziesiętnych wcale nie jest takie straszne, jak się wydaje!