Dzielenie Pisemne Ulamkow Dziesietnych Przyklady

Czy kiedykolwiek stanęliście przed problemem podzielenia kwoty na rachunku ze znajomymi i zastanawialiście się, jak to zrobić precyzyjnie, gdy kwoty są wyrażone w złotych i groszach? A może potrzebowaliście podzielić długość materiału na równe kawałki, gdzie długość była podana w metrach i centymetrach? Zrozumienie dzielenia pisemnego ułamków dziesiętnych jest kluczowe w wielu sytuacjach życia codziennego, a także w edukacji i pracy.

Wiele osób czuje się onieśmielonych, gdy słyszy o dzieleniu pisemnym ułamków dziesiętnych. Wygląda to na skomplikowany proces pełen liczb i przecinków. Ale spokojnie! W tym artykule pokażemy, że dzielenie pisemne ułamków dziesiętnych wcale nie musi być trudne. Krok po kroku przejdziemy przez cały proces, omówimy przykłady i rozwiejemy wszelkie wątpliwości.

Dlaczego Dzielenie Pisemne Ułamków Dziesiętnych Jest Ważne?

Dzielenie pisemne ułamków dziesiętnych to umiejętność, która przydaje się nie tylko w szkole. Oto kilka przykładów z życia wziętych:

Finanse osobiste: Podział rachunku w restauracji, obliczanie raty kredytu, przeliczanie kursów walut.
Zakupy: Porównywanie cen jednostkowych produktów (np. cena za kilogram), obliczanie rabatów.
Gotowanie: Dostosowywanie przepisów na różne ilości porcji, odmierzanie składników.
Praca: Obliczenia inżynieryjne, analizy finansowe, statystyka.

Zatem, umiejętność dzielenia pisemnego ułamków dziesiętnych to praktyczna umiejętność, która ułatwia nam codzienne życie i otwiera drzwi do wielu zawodów.

Jak Dzielić Pisemnie Ułamki Dziesiętne – Krok po Kroku

Proces dzielenia pisemnego ułamków dziesiętnych może wydawać się skomplikowany na pierwszy rzut oka, ale z odpowiednim podejściem i kilkoma prostymi zasadami, szybko stanie się jasny i zrozumiały. Omówimy go krok po kroku:

Krok 1: Przygotowanie do Dzielenia

Pierwszym krokiem jest zapisanie działania w postaci dzielenia pisemnego. Upewnij się, że dzielna (liczba, którą dzielimy) i dzielnik (liczba, przez którą dzielimy) są zapisane poprawnie.

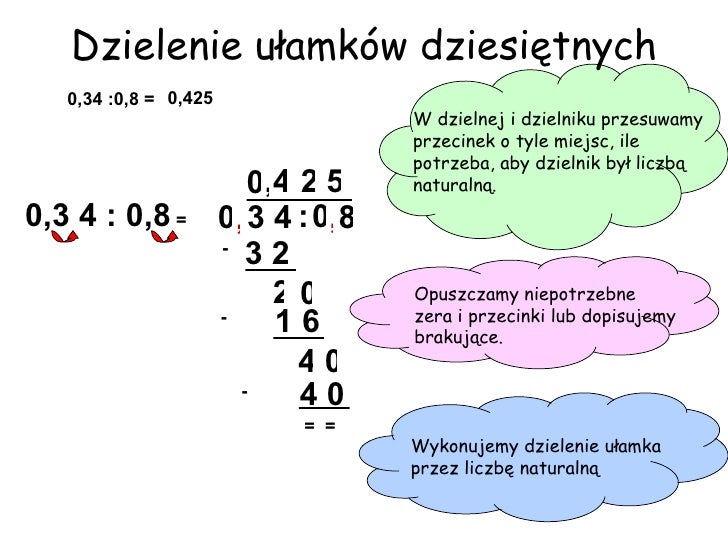
Jeśli dzielnik jest ułamkiem dziesiętnym, musimy go przekształcić w liczbę całkowitą. Robimy to, przesuwając przecinek w dzielniku w prawo, aż do uzyskania liczby całkowitej. Pamiętaj! O tyle samo miejsc musimy przesunąć przecinek w dzielnej.

Przykład: Chcemy podzielić 12,45 przez 2,5. Przesuwamy przecinek w dzielniku (2,5) o jedno miejsce w prawo, aby otrzymać 25. W dzielnej (12,45) również przesuwamy przecinek o jedno miejsce w prawo, otrzymując 124,5.

Krok 2: Dzielenie Jak Liczb Całkowitych

Po przekształceniu dzielnika w liczbę całkowitą, możemy przystąpić do dzielenia jak liczb całkowitych. Ignorujemy na razie przecinek w dzielnej.

Przykład: Dzielimy 124 przez 25. Pytamy: Ile razy 25 mieści się w 124? Odpowiedź to 4 (bo 4 * 25 = 100). Zapisujemy 4 nad kreską, a pod 124 zapisujemy 100. Odejmujemy 100 od 124, co daje nam 24.

Krok 3: Przecinek w Wyniku

Gdy dojdziemy do momentu, w którym musimy "zejść" za przecinek w dzielnej, stawiamy przecinek w wyniku (nad kreską). Następnie kontynuujemy dzielenie, tak jakby przecinka nie było.

Przykład: Mamy 24, a musimy "zejść" za przecinek w dzielnej (124,5), więc stawiamy przecinek w wyniku po 4. Teraz "zejmujemy" 5 z dzielnej, otrzymując 245. Pytamy: Ile razy 25 mieści się w 245? Odpowiedź to 9 (bo 9 * 25 = 225). Zapisujemy 9 nad kreską za przecinkiem, a pod 245 zapisujemy 225. Odejmujemy 225 od 245, co daje nam 20.

Krok 4: Kontynuacja Dzielenia

Jeśli po odjęciu otrzymamy resztę różną od zera, możemy kontynuować dzielenie, dopisując zera po przecinku w dzielnej (pamiętaj, że 124,5 to to samo co 124,50, 124,500 itd.).

Przykład: Mamy 20, dopisujemy 0, otrzymując 200. Pytamy: Ile razy 25 mieści się w 200? Odpowiedź to 8 (bo 8 * 25 = 200). Zapisujemy 8 nad kreską za 9, a pod 200 zapisujemy 200. Odejmujemy 200 od 200, co daje nam 0. Dzielenie zakończone!

Wynik: 12,45 / 2,5 = 4,98

Przykłady Dzielenia Pisemnego Ułamków Dziesiętnych

Aby lepiej zrozumieć proces dzielenia pisemnego ułamków dziesiętnych, przeanalizujmy kilka dodatkowych przykładów:

Przykład 1: 3,6 / 0,4

Przesuwamy przecinek w dzielniku (0,4) o jedno miejsce w prawo, aby otrzymać 4. Przesuwamy przecinek w dzielnej (3,6) o jedno miejsce w prawo, otrzymując 36.
Dzielimy 36 przez 4. Ile razy 4 mieści się w 36? Odpowiedź to 9.
Zapisujemy 9 nad kreską. 36 - (9 * 4) = 0.
Wynik: 3,6 / 0,4 = 9

Przykład 2: 15,75 / 3

Dzielnik (3) jest liczbą całkowitą, więc nie musimy przesuwać przecinka.
Dzielimy 15 przez 3. Ile razy 3 mieści się w 15? Odpowiedź to 5.
Zapisujemy 5 nad kreską. 15 - (5 * 3) = 0.
"Schodzimy" za przecinek w dzielnej, więc stawiamy przecinek w wyniku po 5.
"Zejmujemy" 7. Dzielimy 7 przez 3. Ile razy 3 mieści się w 7? Odpowiedź to 2.
Zapisujemy 2 nad kreską za przecinkiem. 7 - (2 * 3) = 1.
"Zejmujemy" 5. Dzielimy 15 przez 3. Ile razy 3 mieści się w 15? Odpowiedź to 5.
Zapisujemy 5 nad kreską za 2. 15 - (5 * 3) = 0.
Wynik: 15,75 / 3 = 5,25

Przykład 3: 0,24 / 0,08

Przesuwamy przecinek w dzielniku (0,08) o dwa miejsca w prawo, aby otrzymać 8. Przesuwamy przecinek w dzielnej (0,24) o dwa miejsca w prawo, otrzymując 24.
Dzielimy 24 przez 8. Ile razy 8 mieści się w 24? Odpowiedź to 3.
Zapisujemy 3 nad kreską. 24 - (3 * 8) = 0.
Wynik: 0,24 / 0,08 = 3

Częste Błędy i Jak Ich Unikać

Podczas dzielenia pisemnego ułamków dziesiętnych często popełniane są pewne błędy. Zwróć uwagę na te punkty, aby uniknąć pomyłek:

Zapominanie o przesunięciu przecinka: Najważniejsze jest, aby pamiętać o przesunięciu przecinka zarówno w dzielniku, jak i w dzielnej, o tę samą liczbę miejsc.
Błędne umieszczanie przecinka w wyniku: Przecinek w wyniku stawiamy w momencie, gdy "schodizmy" za przecinek w dzielnej.
Pomijanie zer: Jeśli po odjęciu otrzymamy resztę, a nie mamy już więcej cyfr w dzielnej, musimy dopisywać zera i kontynuować dzielenie.
Niepoprawne odejmowanie: Błędy w odejmowaniu prowadzą do niepoprawnego wyniku. Upewnij się, że odejmujesz prawidłowo.

Alternatywne Metody Dzielenia Ułamków Dziesiętnych

Oprócz dzielenia pisemnego, istnieją inne metody dzielenia ułamków dziesiętnych:

Kalkulator: Najprostsza i najszybsza metoda, szczególnie przydatna przy skomplikowanych obliczeniach.
Konwersja na ułamki zwykłe: Ułamki dziesiętne można zamienić na ułamki zwykłe, a następnie podzielić ułamki zwykłe.
Dzielenie w pamięci (w prostych przypadkach): W przypadku prostych przykładów, takich jak 0,5 / 0,1, można łatwo podzielić ułamki w pamięci.

Jednak dzielenie pisemne jest ważne, ponieważ rozwija umiejętności logicznego myślenia i pozwala zrozumieć istotę dzielenia.

Podsumowanie i Dalsze Kroki

Dzielenie pisemne ułamków dziesiętnych to umiejętność, która przydaje się w wielu sytuacjach życiowych. Choć może wydawać się trudne na początku, z odpowiednim podejściem i praktyką staje się proste i zrozumiałe. Pamiętaj o przesuwaniu przecinka, poprawnym umieszczaniu przecinka w wyniku i dopisywaniu zer, jeśli to konieczne.

Ćwiczenie czyni mistrza! Spróbuj rozwiązać kilka przykładów samodzielnie, korzystając z omówionych kroków. Jeśli masz jakiekolwiek pytania, śmiało pytaj nauczyciela, kolegę lub szukaj odpowiedzi w Internecie.

Czy ten artykuł pomógł Ci lepiej zrozumieć dzielenie pisemne ułamków dziesiętnych? Jakie zagadnienia związane z matematyką chciałbyś, abyśmy omówili w przyszłości?