Działania W Zbiorach Liczbowych Sprawdzian Liceum Pazdro

Dzień dobry wszystkim! Wiem, że działania w zbiorach liczbowych mogą wydawać się na początku trudne, szczególnie na sprawdzianie. Spróbuję to wszystko wyjaśnić w prosty i przystępny sposób, żebyście poczuli się pewniej. Skupimy się na tym, jak rozwiązywać typowe zadania, które mogą się pojawić. Pamiętajcie, najważniejsza jest praktyka, więc im więcej ćwiczeń zrobicie, tym lepiej.

Zacznijmy od podstaw. Co to właściwie są zbiory liczbowe? Mówiąc najprościej, to grupy liczb, które mają jakieś wspólne cechy. Mamy zbiór liczb naturalnych (1, 2, 3...), całkowitych (..., -2, -1, 0, 1, 2...), wymiernych (dają się zapisać jako ułamek), niewymiernych (np. √2, π) i wreszcie, zbiór liczb rzeczywistych, który zawiera wszystkie wymienione wcześniej.

Na sprawdzianie najczęściej pojawiają się zadania, gdzie trzeba wykonywać operacje na liczbach z różnych zbiorów i sprawdzać, do jakiego zbioru należy wynik. Trzeba umieć dodawać, odejmować, mnożyć, dzielić, potęgować i pierwiastkować. I pamiętać o kolejności wykonywania działań!

Działania na ułamkach

Ułamki to częsty element zadań. Dodawanie i odejmowanie ułamków wymaga sprowadzenia ich do wspólnego mianownika. Żeby znaleźć wspólny mianownik, szukamy najmniejszej wspólnej wielokrotności (NWW) mianowników. Na przykład, żeby dodać 1/2 i 1/3, musimy znaleźć NWW liczb 2 i 3, która wynosi 6. Wtedy zamieniamy 1/2 na 3/6, a 1/3 na 2/6. Teraz możemy dodać: 3/6 + 2/6 = 5/6.

Mnożenie ułamków jest prostsze – mnożymy licznik razy licznik, a mianownik razy mianownik. Na przykład, 1/2 * 1/3 = 1/6.

Dzielenie ułamków to mnożenie przez odwrotność drugiego ułamka. Czyli, jeśli mamy 1/2 : 1/3, to zamieniamy to na 1/2 * 3/1 = 3/2.

Potęgi i pierwiastki

Potęgi to skrócony zapis mnożenia tej samej liczby przez siebie. Na przykład, 2 do potęgi 3 (czyli 2³) to 2 * 2 * 2 = 8. Trzeba pamiętać o zasadach dotyczących potęg o wykładnikach ujemnych i ułamkowych. Liczba do potęgi ujemnej to odwrotność tej liczby podniesionej do potęgi dodatniej. Czyli, 2⁻¹ to 1/2. Liczba do potęgi ułamkowej to pierwiastek. Na przykład, 4¹/² to √4 = 2.

Pierwiastki to odwrotność potęgowania. Pierwiastek kwadratowy z liczby to taka liczba, która pomnożona przez siebie daje liczbę pod pierwiastkiem. Na przykład, √9 = 3, bo 3 * 3 = 9. Trzeba uważać na pierwiastki z liczb ujemnych – w zbiorze liczb rzeczywistych nie istnieją pierwiastki kwadratowe z liczb ujemnych. Istnieją one natomiast w zbiorze liczb zespolonych.

Wyrażenia algebraiczne

Często na sprawdzianie pojawiają się zadania z wyrażeniami algebraicznymi, gdzie mamy litery (zmienne) i liczby połączone działaniami. Trzeba umieć upraszczać takie wyrażenia, redukować wyrazy podobne (czyli te, które mają tę samą literę w tej samej potędze) i rozkładać wyrażenia na czynniki. Na przykład, 2x + 3x - 5 + 2 to 5x - 3.

Rozkładanie na czynniki polega na znalezieniu wspólnego czynnika w kilku wyrazach i wyłączeniu go przed nawias. Na przykład, w wyrażeniu 4x + 6y wspólnym czynnikiem jest 2. Możemy więc zapisać to jako 2(2x + 3y). Ważne są też wzory skróconego mnożenia, takie jak (a + b)² = a² + 2ab + b² i (a - b)² = a² - 2ab + b² oraz (a + b)(a - b) = a² - b². Znajomość tych wzorów bardzo ułatwia rozwiązywanie zadań.

Przykłady zadań i ich rozwiązywanie

1. Sprawdź, czy liczba √2 + √8 jest liczbą wymierną.

   Najpierw uprośćmy √8. √8 = √(4 * 2) = √4 * √2 = 2√2. Teraz dodajemy: √2 + 2√2 = 3√2. Liczba 3√2 jest liczbą niewymierną, bo √2 jest niewymierne, a iloczyn liczby wymiernej i niewymiernej jest niewymierny (z wyjątkiem przypadku mnożenia przez zero).

2. Oblicz (1/2 + 1/3) : 5/6.

   Najpierw obliczamy sumę w nawiasie: 1/2 + 1/3 = 3/6 + 2/6 = 5/6. Teraz dzielimy: 5/6 : 5/6 = 5/6 * 6/5 = 1.

3. Uprość wyrażenie (x + 2)² - x²

   Korzystamy ze wzoru skróconego mnożenia: (x + 2)² = x² + 4x + 4. Teraz odejmujemy: x² + 4x + 4 - x² = 4x + 4.

4. Rozwiąż nierówność |x - 1| < 2

   Oznacza to, że odległość x od 1 jest mniejsza niż 2. Możemy to zapisać jako dwie nierówności: -2 < x - 1 < 2. Dodajemy 1 do każdej strony: -1 < x < 3. Rozwiązaniem jest więc przedział (-1, 3).

5. Określ dziedzinę funkcji f(x) = 1/(x-3)

   Dziedzina funkcji to zbiór wszystkich argumentów (x), dla których funkcja ma sens. W tym przypadku, mianownik nie może być równy zero, bo nie można dzielić przez zero. Czyli, x - 3 ≠ 0, co oznacza, że x ≠ 3. Dziedziną funkcji jest więc zbiór wszystkich liczb rzeczywistych z wyjątkiem 3, czyli R \ {3}.

Pamiętajcie, żeby dokładnie czytać treść zadania i zwracać uwagę na szczegóły. Często błędy wynikają z niedokładnego przeczytania zadania, a nie z braku wiedzy.

Kilka dodatkowych wskazówek

• Używaj brudnopisu: Nie bój się robić obliczeń na brudnopisie. Lepiej sprawdzić kilka razy, niż popełnić błąd z pośpiechu.
• Sprawdzaj wyniki: Po rozwiązaniu zadania, spróbuj sprawdzić, czy wynik ma sens. Możesz na przykład podstawić obliczoną wartość do oryginalnego równania i sprawdzić, czy się zgadza.
• Zacznij od najłatwiejszych zadań: Na sprawdzianie zacznij od zadań, które wydają ci się najłatwiejsze. To pomoże ci się rozgrzać i nabrać pewności siebie. Potem możesz przejść do trudniejszych zadań.
• Nie panikuj: Jeśli utkniesz na jakimś zadaniu, nie panikuj. Spróbuj jeszcze raz przeczytać treść zadania, zastanów się, jakie wzory lub zasady możesz zastosować. Jeśli nadal nie wiesz, jak rozwiązać zadanie, przejdź do następnego i wróć do niego później.
• Pamiętaj o jednostkach: Jeśli zadanie dotyczy wielkości fizycznych (np. długości, masy, czasu), pamiętaj o podaniu jednostek.

Wartość bezwzględna liczby to jej odległość od zera na osi liczbowej. Oznacza się ją pionowymi kreskami: |x|. Wartość bezwzględna zawsze jest nieujemna. Na przykład, |3| = 3, a |-3| = 3.

Zadania z wartością bezwzględną często polegają na rozwiązywaniu równań i nierówności. Trzeba pamiętać, że wartość bezwzględna "kasuje" znak minus.

Przykład:

|x - 2| = 3

To równanie oznacza, że odległość x od 2 wynosi 3. Istnieją dwie możliwości:

• x - 2 = 3, czyli x = 5
• x - 2 = -3, czyli x = -1

Rozwiązaniem są więc dwie liczby: 5 i -1.

Podobnie rozwiązuje się nierówności. Na przykład:

|x + 1| < 2

Oznacza to, że odległość x od -1 jest mniejsza niż 2. Możemy to zapisać jako dwie nierówności:

-2 < x + 1 < 2

Odejmujemy 1 od każdej strony:

-3 < x < 1

Rozwiązaniem jest więc przedział (-3, 1).

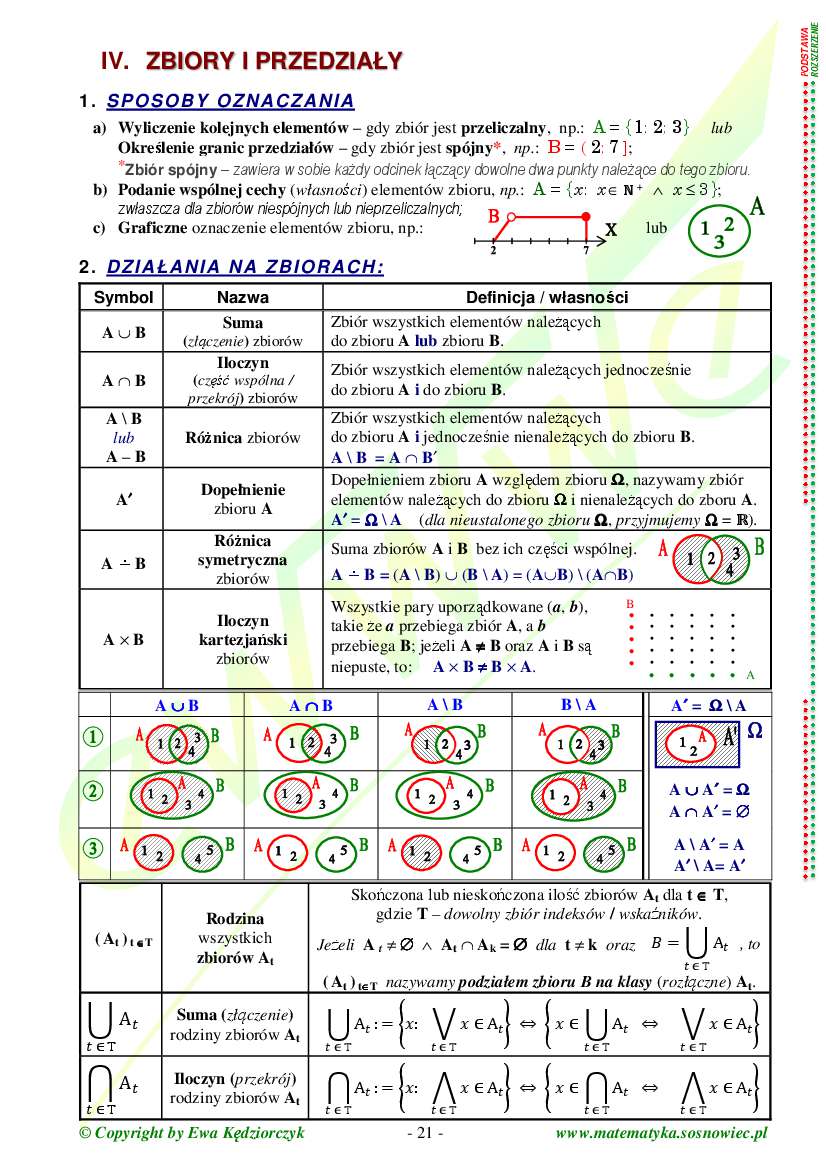
Często spotykane są zadania, które sprawdzają waszą umiejętność operowania na zbiorach. Mamy kilka podstawowych operacji:

• Suma zbiorów (A ∪ B): To zbiór, który zawiera wszystkie elementy zbioru A i wszystkie elementy zbioru B.
• Iloczyn zbiorów (A ∩ B): To zbiór, który zawiera tylko te elementy, które należą zarówno do zbioru A, jak i do zbioru B.
• Różnica zbiorów (A \ B): To zbiór, który zawiera tylko te elementy, które należą do zbioru A, ale nie należą do zbioru B.
• Dopełnienie zbioru (A'): To zbiór, który zawiera wszystkie elementy, które nie należą do zbioru A (ale należą do przestrzeni, w której rozważamy zbiory).

Przykład:

A = {1, 2, 3, 4}

B = {3, 4, 5, 6}

A ∪ B = {1, 2, 3, 4, 5, 6}

A ∩ B = {3, 4}

A \ B = {1, 2}

Zakładając, że przestrzenią jest zbiór liczb naturalnych, dopełnienie zbioru A jest zbiorem wszystkich liczb naturalnych, które nie należą do A (czyli {5, 6, 7, 8...}).

Pamiętajcie, kluczem do sukcesu jest zrozumienie podstawowych pojęć i regularne ćwiczenia. Przeróbcie zadania z podręcznika, rozwiążcie arkusze z poprzednich lat i analizujcie swoje błędy. Im więcej będziecie ćwiczyć, tym pewniej poczujecie się na sprawdzianie. Trzymam za was kciuki! Powodzenia!