Działania Na Ułamkach Zwykłych Klasa 6

Czy kiedykolwiek miałeś problem z podzieleniem pizzy sprawiedliwie między przyjaciół? A może zastanawiałeś się, ile składników potrzebujesz, gdy przepis jest podany tylko na połowę porcji? Jeśli tak, to wiedz, że zmagasz się z **ułamkami zwykłymi**! Dla wielu uczniów klasy 6 to zagadnienie wydaje się trudne i abstrakcyjne, ale w rzeczywistości ułamki są wszędzie wokół nas i umiejętność operowania nimi jest niezwykle przydatna w życiu codziennym.
Dlaczego ułamki sprawiają trudności?
Zanim przejdziemy do konkretnych działań, warto zrozumieć, skąd bierze się trudność. Często problemem jest samo pojęcie ułamka – co tak naprawdę oznacza zapis typu 1/2 czy 3/4? Innym wyzwaniem jest zapamiętanie wszystkich zasad dotyczących dodawania, odejmowania, mnożenia i dzielenia ułamków. A przecież to wszystko ma sens!
Pomyślmy o ułamku jako o części czegoś. 1/2 pizzy to połowa pizzy. 3/4 szklanki soku to trzy z czterech równych części szklanki. Wizualizacja pomaga zrozumieć, o czym mówimy.
Podstawowe pojęcia – przypomnienie
Zanim przejdziemy do działań, upewnijmy się, że rozumiemy podstawowe pojęcia:
- Licznik: liczba znajdująca się nad kreską ułamkową. Mówi nam, ile części bierzemy pod uwagę (np. 3 w ułamku 3/4).
- Mianownik: liczba znajdująca się pod kreską ułamkową. Mówi nam, na ile równych części podzielona jest całość (np. 4 w ułamku 3/4).
- Kreska ułamkowa: oznacza dzielenie. Ułamek 3/4 to to samo, co 3 podzielone przez 4.
Pamiętajmy również o pojęciu ułamka właściwego (licznik jest mniejszy od mianownika, np. 1/2) i ułamka niewłaściwego (licznik jest większy lub równy mianownikowi, np. 5/4). Ułamek niewłaściwy możemy zamienić na liczbę mieszaną (np. 5/4 = 1 1/4).
Działania na ułamkach – krok po kroku
Przejdźmy teraz do sedna, czyli do wykonywania działań na ułamkach zwykłych. Skupimy się na każdym działaniu osobno, podając jasne zasady i przykłady.
Dodawanie i odejmowanie ułamków
To tutaj wielu uczniów napotyka na problemy. Najważniejsza zasada brzmi: możemy dodawać i odejmować tylko ułamki o tym samym mianowniku!
Jeśli mianowniki są różne, musimy je sprowadzić do wspólnego mianownika.
Jak sprowadzić ułamki do wspólnego mianownika? Możemy to zrobić, znajdując najmniejszą wspólną wielokrotność (NWW) mianowników. Pamiętasz NWW z poprzednich lekcji? Jeśli nie, warto sobie to przypomnieć! Innym sposobem jest pomnożenie każdego ułamka przez odpowiedni ułamek równy 1 (np. 2/2, 3/3), aby otrzymać ten sam mianownik.
Przykład:
Chcemy dodać 1/2 + 1/3.
- Znajdujemy wspólny mianownik. NWW dla 2 i 3 to 6.
- Sprowadzamy ułamki do wspólnego mianownika: 1/2 = 3/6 (mnożymy licznik i mianownik przez 3) oraz 1/3 = 2/6 (mnożymy licznik i mianownik przez 2).
- Teraz możemy dodać: 3/6 + 2/6 = 5/6.
Odejmowanie działa dokładnie tak samo – sprowadzamy do wspólnego mianownika i odejmujemy liczniki.
Mnożenie ułamków
Mnożenie ułamków jest prostsze niż dodawanie i odejmowanie. Po prostu mnożymy licznik przez licznik, a mianownik przez mianownik.
Przykład:
2/3 * 1/4 = (2 * 1) / (3 * 4) = 2/12
Pamiętaj, że wynik warto uprościć (skrócić ułamek), dzieląc licznik i mianownik przez ten sam dzielnik. W naszym przykładzie 2/12 można skrócić do 1/6.
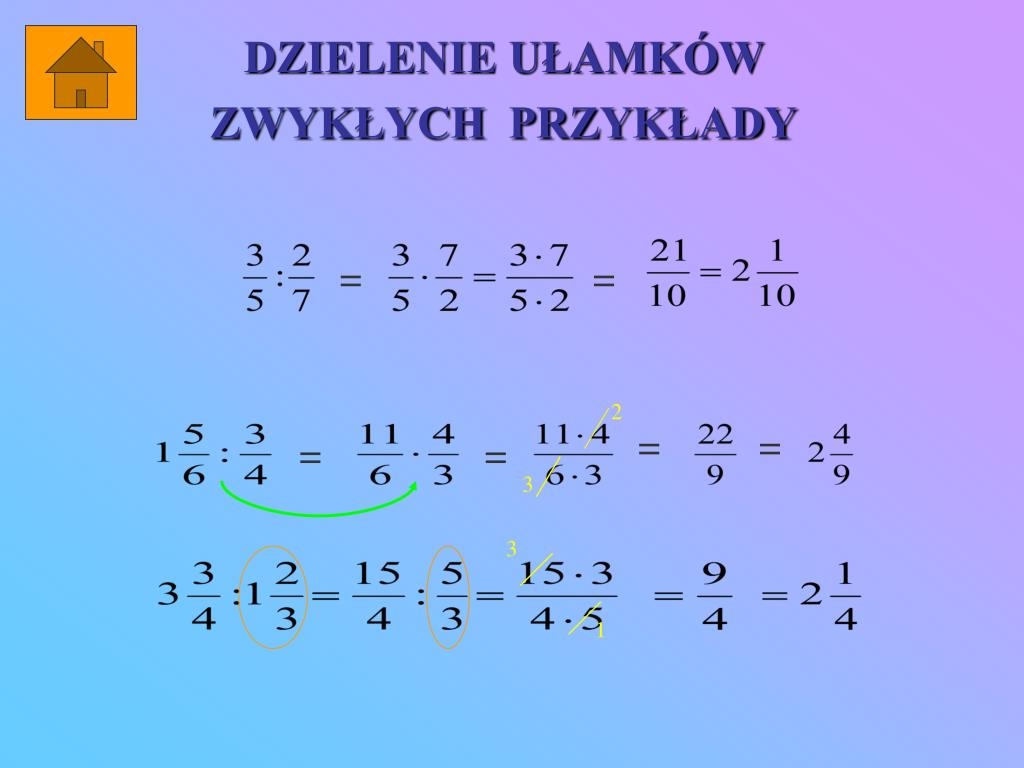
Dzielenie ułamków
Dzielenie ułamków to tak naprawdę... mnożenie! Dzieląc przez ułamek, mnożymy przez jego odwrotność.
Co to jest odwrotność ułamka? To ułamek, w którym zamieniamy licznik z mianownikiem. Odwrotnością 2/3 jest 3/2.
Przykład:
1/2 : 1/4 = 1/2 * 4/1 = (1 * 4) / (2 * 1) = 4/2 = 2
Ułamki a życie codzienne – gdzie je spotykamy?
Jak wspomnieliśmy na początku, ułamki są obecne w wielu sytuacjach życiowych. Oto kilka przykładów:
- Gotowanie i pieczenie: przepisy często podają proporcje składników w ułamkach (np. pół szklanki mąki, ćwierć łyżeczki soli).
- Zakupy: promocje typu "kup dwa, zapłać za półtora" wykorzystują ułamki.
- Mierzenie: długość, waga, objętość – często wyrażane są za pomocą ułamków.
- Podział obowiązków: dzielenie zadań między członków rodziny lub zespołu.
- Planowanie czasu: określanie, ile czasu poświęcamy na poszczególne czynności (np. pół godziny na odrabianie lekcji).
Częste błędy i jak ich unikać
Pamiętajmy o typowych pułapkach, w które łatwo wpaść przy operacjach na ułamkach:
- Zapominanie o sprowadzaniu do wspólnego mianownika: to najczęstszy błąd przy dodawaniu i odejmowaniu.
- Mnożenie lub dzielenie tylko jednego elementu ułamka przy sprowadzaniu do wspólnego mianownika: musimy pamiętać o pomnożeniu zarówno licznika, jak i mianownika.
- Błędne upraszczanie ułamków: dzielimy licznik i mianownik przez ten sam dzielnik.
- Zapominanie o odwrotności przy dzieleniu.
Ćwiczenie czyni mistrza! Im więcej przykładów rozwiążesz, tym lepiej zrozumiesz zasady i unikniesz błędów.
Przykładowe zadania z rozwiązaniami
Aby utrwalić wiedzę, przeanalizujmy kilka zadań:
Zadanie 1: Mama upiekła ciasto i podzieliła je na 8 równych części. Zosia zjadła 1/4 ciasta, a Tomek 3/8. Ile ciasta zjedli razem?
Rozwiązanie:
- Sprowadzamy ułamki do wspólnego mianownika: 1/4 = 2/8.
- Dodajemy ułamki: 2/8 + 3/8 = 5/8.
- Odpowiedź: Zosia i Tomek zjedli razem 5/8 ciasta.
Zadanie 2: Kasia ma 2/3 szklanki soku. Chce podzielić go równo między 4 osoby. Ile soku otrzyma każda osoba?
Rozwiązanie:
- Dzielimy ułamek: 2/3 : 4 = 2/3 * 1/4 = 2/12.
- Upraszczamy ułamek: 2/12 = 1/6.
- Odpowiedź: Każda osoba otrzyma 1/6 szklanki soku.
Podsumowanie i dalsze kroki
Ułamki zwykłe to ważna część matematyki, która ma wiele zastosowań w życiu codziennym. Pamiętaj o podstawowych zasadach, ćwicz regularnie i nie bój się zadawać pytań! Zrozumienie ułamków otworzy Ci drzwi do bardziej zaawansowanych zagadnień matematycznych.
Jeśli nadal masz trudności, poszukaj dodatkowych materiałów, np. ćwiczeń online, filmów edukacyjnych lub poproś o pomoc nauczyciela lub starszego kolegę. Pamiętaj, że nikt nie urodził się z wiedzą o ułamkach – wszystko wymaga praktyki i cierpliwości.
Na koniec, zastanów się: w jakiej sytuacji w najbliższym czasie możesz wykorzystać swoją wiedzę o ułamkach? Spróbuj rozwiązać jakiś problem, który dotychczas wydawał się trudny, dzięki nowo nabytym umiejętnościom. Powodzenia!