Działania Na Ułamkach Zwykłych I Dziesiętnych Klasa 6 Karta Pracy

Ułamki zwykłe i dziesiętne stanowią fundament wiedzy matematycznej, szczególnie istotny w klasie 6. Zrozumienie operacji na tych liczbach jest kluczowe dla dalszego sukcesu w matematyce i dla praktycznego zastosowania w życiu codziennym. Niniejszy artykuł ma na celu omówienie działań na ułamkach zwykłych i dziesiętnych, z uwzględnieniem zasad, przykładów i praktycznych zastosowań, ze szczególnym naciskiem na materiał zawarty w karcie pracy dla klasy 6.

Podstawowe operacje na ułamkach zwykłych

Ułamki zwykłe, reprezentowane w postaci a/b (gdzie a to licznik, a b to mianownik), podlegają podstawowym operacjom arytmetycznym. Sprawne wykonywanie tych działań jest niezbędne do rozwiązywania bardziej złożonych problemów.

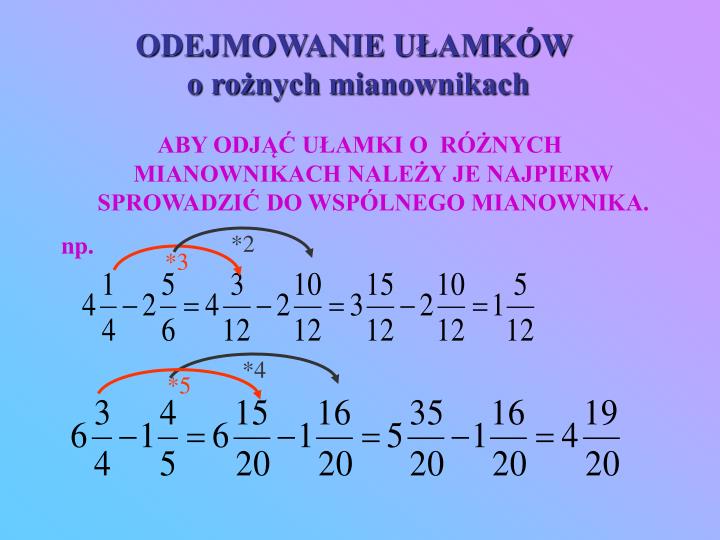
Dodawanie i odejmowanie ułamków zwykłych

Dodawanie i odejmowanie ułamków wymaga sprowadzenia ich do wspólnego mianownika. Jeśli ułamki mają różne mianowniki, należy znaleźć najmniejszą wspólną wielokrotność (NWW) mianowników i rozszerzyć ułamki tak, aby miały ten sam mianownik. Następnie dodajemy lub odejmujemy liczniki, a mianownik pozostaje bez zmian. Przykładowo:

1/3 + 1/4 = 4/12 + 3/12 = 7/12
2/5 - 1/10 = 4/10 - 1/10 = 3/10

Warto pamiętać o upraszczaniu wyniku, jeśli to możliwe. Jeśli wynik jest ułamkiem niewłaściwym (licznik większy od mianownika), można go zamienić na liczbę mieszaną.

Mnożenie ułamków zwykłych

Mnożenie ułamków jest stosunkowo proste. Mnożymy licznik przez licznik i mianownik przez mianownik. Nie trzeba sprowadzać do wspólnego mianownika. Przykładowo:

2/3 * 3/4 = (2 * 3) / (3 * 4) = 6/12 = 1/2

Przed wykonaniem mnożenia, warto sprawdzić, czy można skrócić ułamki "na krzyż", czyli podzielić licznik jednego ułamka i mianownik drugiego ułamka przez ich wspólny dzielnik. Upraszcza to obliczenia.

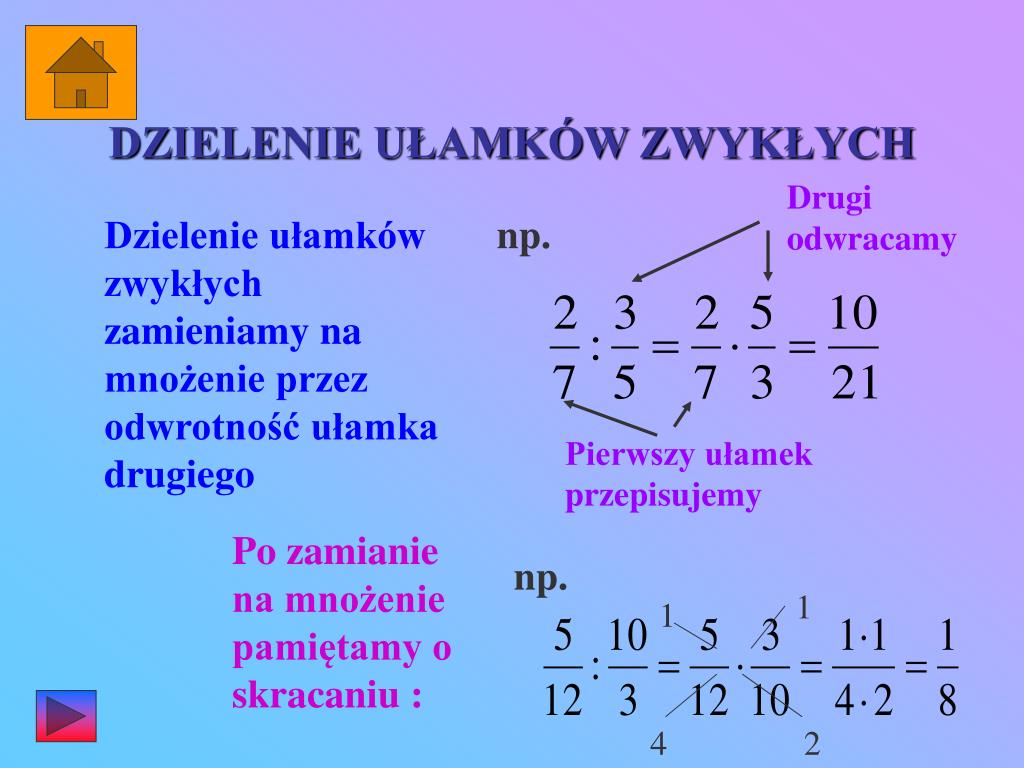
Dzielenie ułamków zwykłych

Dzielenie ułamków to mnożenie przez odwrotność drugiego ułamka. Oznacza to, że dzieląc ułamek a/b przez ułamek c/d, mnożymy a/b przez d/c. Przykładowo:

1/2 : 2/3 = 1/2 * 3/2 = 3/4

Podobnie jak przy mnożeniu, warto sprawdzić, czy można skrócić ułamki przed wykonaniem mnożenia.

Operacje na ułamkach dziesiętnych

Ułamki dziesiętne, zapisywane z użyciem przecinka, również podlegają podstawowym działaniom arytmetycznym. Zrozumienie ich zapisu i operacji na nich jest kluczowe.

Dodawanie i odejmowanie ułamków dziesiętnych

Dodawanie i odejmowanie ułamków dziesiętnych wymaga równego ustawienia przecinków w dodawanych lub odejmowanych liczbach. Można dopisać zera, aby wyrównać liczbę cyfr po przecinku. Następnie dodajemy lub odejmujemy jak liczby całkowite, pamiętając o przeniesieniu przecinka w wynik tak, aby znajdował się w tym samym miejscu, co w dodawanych lub odejmowanych liczbach. Przykładowo:

1,25 + 3,1 = 1,25 + 3,10 = 4,35
5,7 - 2,32 = 5,70 - 2,32 = 3,38

Mnożenie ułamków dziesiętnych

Mnożenie ułamków dziesiętnych wykonujemy jak mnożenie liczb całkowitych, ignorując przecinek. Następnie w wyniku oddzielamy przecinkiem tyle cyfr od prawej strony, ile łącznie znajduje się cyfr po przecinku w mnożonych liczbach. Przykładowo:

2,5 * 1,2 = 300
2, 5 (1 cyfra po przecinku)
* 1, 2 (1 cyfra po przecinku)
= 3, 00 (2 cyfry po przecinku)

Zatem 2,5 * 1,2 = 3,00 = 3.

Dzielenie ułamków dziesiętnych

Dzielenie ułamków dziesiętnych wymaga przesunięcia przecinka w dzielniku i dzielnej o tyle miejsc w prawo, aby dzielnik stał się liczbą całkowitą. Następnie wykonujemy dzielenie jak dzielenie liczb całkowitych. Przykładowo:

4,8 : 1,6 = 48 : 16 = 3
5,25 : 0,5 = 52,5 : 5 = 10,5

Jeśli dzielenie nie daje wyniku całkowitego, możemy kontynuować dzielenie, dopisując zera po przecinku w dzielnej.

Zamiana ułamków zwykłych na dziesiętne i odwrotnie

Umiejętność zamiany ułamków zwykłych na dziesiętne i odwrotnie jest bardzo przydatna przy rozwiązywaniu zadań.

Zamiana ułamka zwykłego na dziesiętny

Ułamek zwykły można zamienić na dziesiętny, dzieląc licznik przez mianownik. Często wygodnie jest najpierw rozszerzyć ułamek zwykły do mianownika 10, 100, 1000, itd. Przykładowo:

1/2 = 5/10 = 0,5
3/4 = 75/100 = 0,75
1/8 = 125/1000 = 0,125

Nie wszystkie ułamki zwykłe dają się zamienić na ułamki dziesiętne skończone. W takich przypadkach otrzymujemy ułamek dziesiętny okresowy. Na przykład 1/3 = 0,333... (zapisywane jako 0,(3)).

Zamiana ułamka dziesiętnego na zwykły

Aby zamienić ułamek dziesiętny na zwykły, zapisujemy go jako ułamek, w którym licznikiem jest liczba bez przecinka, a mianownikiem jest 1 z tyloma zerami, ile cyfr jest po przecinku w ułamku dziesiętnym. Następnie upraszczamy ułamek, jeśli to możliwe. Przykładowo:

0,25 = 25/100 = 1/4
1,5 = 15/10 = 3/2

Karta pracy dla klasy 6 - Przykładowe zadania

Karty pracy dla klasy 6 zawierają różnorodne zadania, które sprawdzają umiejętność wykonywania działań na ułamkach zwykłych i dziesiętnych. Przykładowe zadania mogą obejmować:

Dodawanie i odejmowanie ułamków o różnych mianownikach.
Mnożenie i dzielenie ułamków zwykłych i dziesiętnych.
Zamiana ułamków zwykłych na dziesiętne i odwrotnie.
Porównywanie ułamków.
Rozwiązywanie zadań tekstowych z użyciem ułamków.

Rozwiązanie tych zadań wymaga zastosowania wiedzy teoretycznej w praktyce. Ważne jest, aby krok po kroku analizować treść zadania, wybrać odpowiednie działanie i poprawnie je wykonać. Często pomocne jest rysowanie schematów lub diagramów, które pomagają wizualizować problem.

Praktyczne zastosowania ułamków

Działania na ułamkach mają szerokie zastosowanie w życiu codziennym. Przykłady obejmują:

Gotowanie: odmierzanie składników według przepisów (np. 1/2 szklanki mąki, 0,75 litra mleka).
Zakupy: obliczanie rabatów i obniżek cen (np. 20% zniżki na towar).
Mierzenie: określanie długości, wagi, objętości (np. 2,5 metra materiału, 0,5 kg cukru).
Podział: dzielenie pizzy na równe części, dzielenie budżetu na różne wydatki.
Finanse: obliczanie oprocentowania, spłaty kredytów.

Na przykład, jeśli w sklepie jest promocja -25% na dany produkt, a jego pierwotna cena wynosi 40 zł, możemy obliczyć obniżkę, mnożąc 40 zł przez 0,25 (czyli 25/100), co daje 10 zł. Zatem cena po obniżce wynosi 30 zł.

Badania pokazują, że osoby, które dobrze opanowały operacje na ułamkach, radzą sobie lepiej z zadaniami matematycznymi w dalszej edukacji oraz w życiu zawodowym. Umiejętność posługiwania się ułamkami wpływa na zdolność logicznego myślenia i rozwiązywania problemów.

Podsumowanie i dalsze kroki

Opanowanie działań na ułamkach zwykłych i dziesiętnych to kluczowy element edukacji matematycznej w klasie 6. Regularne ćwiczenia, rozwiązywanie zadań z kart pracy i praktyczne zastosowanie wiedzy teoretycznej pozwolą na utrwalenie zdobytych umiejętności. Pamiętaj o podstawowych zasadach dodawania, odejmowania, mnożenia i dzielenia ułamków, zamianie ułamków zwykłych na dziesiętne i odwrotnie. W razie trudności, nie wahaj się prosić o pomoc nauczyciela lub korzystać z dostępnych materiałów edukacyjnych online. Im lepiej opanujesz te umiejętności, tym łatwiej będzie Ci w dalszej nauce matematyki i w życiu codziennym.

Zachęcamy do systematycznej pracy i rozwiązywania zadań z różnych źródeł. Korzystaj z dostępnych narzędzi, takich jak kalkulatory ułamkowe online, które mogą pomóc w sprawdzeniu poprawności wyników. Pamiętaj, że praktyka czyni mistrza! Powodzenia!