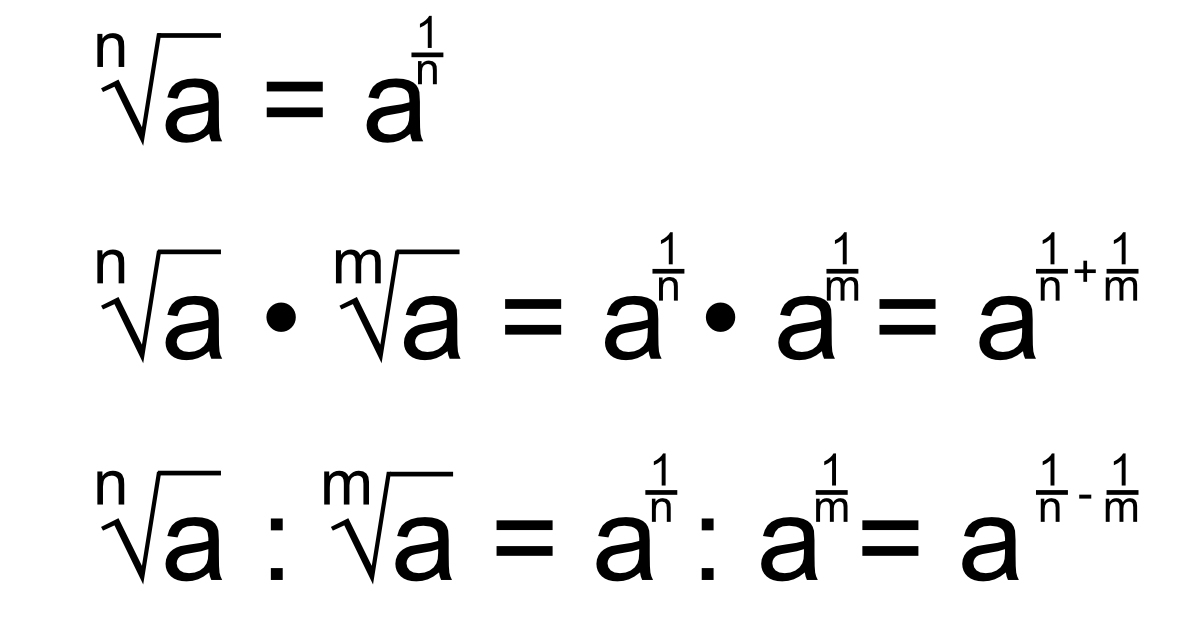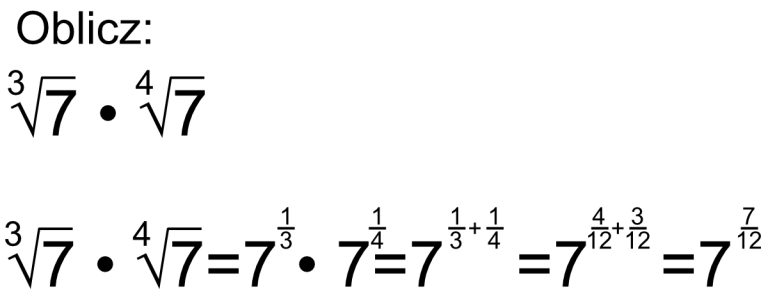Dzialania Na Pierwiastkach Klasa 8

Czy kiedykolwiek zastanawiałeś się, jak uprościć skomplikowane wyrażenia matematyczne, które zawierają pierwiastki kwadratowe i pierwiastki trzeciego stopnia? W ósmej klasie szkoły podstawowej poznajemy fascynujący świat działań na pierwiastkach. Ten artykuł jest skierowany do uczniów ósmej klasy, rodziców wspierających naukę swoich dzieci oraz nauczycieli, którzy chcą znaleźć dodatkowe materiały objaśniające te zagadnienia. Naszym celem jest przystępne wyjaśnienie, jak wykonywać dodawanie, odejmowanie, mnożenie i dzielenie pierwiastków, a także jak je upraszczać.

Co to są pierwiastki? Podstawowe definicje

Zanim przejdziemy do działań, przypomnijmy sobie, czym są pierwiastki. Najczęściej spotykamy się z pierwiastkiem kwadratowym, oznaczanym symbolem √. Pierwiastek kwadratowy z liczby a (√a) to taka liczba, która podniesiona do kwadratu daje a. Na przykład, √9 = 3, ponieważ 3² = 9.

Oprócz pierwiastka kwadratowego, istnieje również pierwiastek trzeciego stopnia, oznaczany symbolem ³√. Pierwiastek trzeciego stopnia z liczby a (³√a) to taka liczba, która podniesiona do trzeciej potęgi daje a. Na przykład, ³√8 = 2, ponieważ 2³ = 8.

Generalnie, pierwiastek n-tego stopnia z liczby a (ⁿ√a) to taka liczba, która podniesiona do potęgi n daje a.

Upraszczanie pierwiastków

Upraszczanie pierwiastków to bardzo ważna umiejętność. Polega na zapisaniu pierwiastka w prostszej formie, wyłączając czynniki przed znak pierwiastka. Spójrzmy na kilka przykładów:

Wyłączanie czynnika przed znak pierwiastka kwadratowego

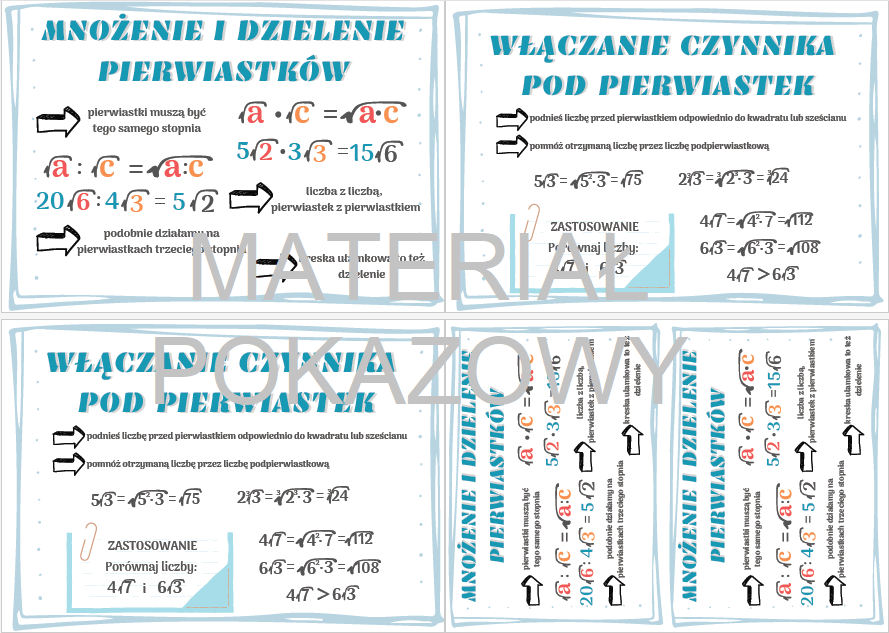
Załóżmy, że mamy √12. Możemy rozłożyć 12 na czynniki pierwsze: 12 = 2 * 2 * 3 = 2² * 3. Zatem:

√12 = √(2² * 3) = √(2²) * √3 = 2√3

Kluczem jest znalezienie idealnego kwadratu, który jest czynnikiem liczby pod pierwiastkiem.

Inny przykład: √75 = √(25 * 3) = √25 * √3 = 5√3

Wyłączanie czynnika przed znak pierwiastka trzeciego stopnia

Teraz spróbujmy z pierwiastkiem trzeciego stopnia. Weźmy ³√24. Rozkładamy 24 na czynniki pierwsze: 24 = 2 * 2 * 2 * 3 = 2³ * 3. Zatem:

³√24 = ³√(2³ * 3) = ³√(2³) * ³√3 = 2 ³√3

Tutaj szukamy idealnej trzeciej potęgi.

Kolejny przykład: ³√81 = ³√(27 * 3) = ³√27 * ³√3 = 3 ³√3

Działania na pierwiastkach

Gdy już potrafimy upraszczać pierwiastki, możemy przejść do wykonywania na nich działań. Pamiętajmy, że nie zawsze możemy od razu dodać lub odjąć pierwiastki.

Dodawanie i odejmowanie pierwiastków

Możemy dodawać i odejmować tylko te pierwiastki, które mają taki sam stopień i tę samą liczbę pod pierwiastkiem. Innymi słowy, musimy mieć "podobne" pierwiastki.

Przykłady:

• 2√3 + 5√3 = (2 + 5)√3 = 7√3
• 7√2 - 3√2 = (7 - 3)√2 = 4√2

Co zrobić, jeśli pierwiastki nie są "podobne"? Najpierw próbujemy je uprościć!

Przykład: √12 + √27

Upraszczamy:

• √12 = 2√3
• √27 = √(9 * 3) = 3√3

Teraz możemy dodać: 2√3 + 3√3 = 5√3

Mnożenie pierwiastków

Mnożenie pierwiastków jest prostsze niż dodawanie i odejmowanie. Możemy mnożyć pierwiastki tego samego stopnia. Mnożymy wtedy liczby pod pierwiastkami.

Przykłady:

• √2 * √3 = √(2 * 3) = √6
• 2√5 * 3√7 = (2 * 3)√(5 * 7) = 6√35
• ³√4 * ³√2 = ³√(4 * 2) = ³√8 = 2

Dzielenie pierwiastków

Podobnie jak mnożenie, dzielenie pierwiastków wymaga, aby pierwiastki były tego samego stopnia. Dzielimy wtedy liczby pod pierwiastkami.

Przykłady:

• √10 / √2 = √(10 / 2) = √5
• 6√15 / 2√3 = (6 / 2)√(15 / 3) = 3√5
• ³√24 / ³√3 = ³√(24 / 3) = ³√8 = 2

Usuwanie niewymierności z mianownika

Często w zadaniach matematycznych dąży się do tego, aby w mianowniku ułamka nie było pierwiastka. Proces usuwania pierwiastka z mianownika nazywamy usuwaniem niewymierności z mianownika.

Jak to zrobić?

Mianownik z pojedynczym pierwiastkiem kwadratowym

Jeśli w mianowniku mamy pojedynczy pierwiastek kwadratowy, mnożymy licznik i mianownik przez ten pierwiastek.

Przykład: 1/√2

Mnożymy licznik i mianownik przez √2:

(1 * √2) / (√2 * √2) = √2 / 2

Mianownik w postaci sumy lub różnicy z pierwiastkiem kwadratowym

Jeśli w mianowniku mamy sumę lub różnicę, w której występuje pierwiastek kwadratowy, wykorzystujemy wzór na różnicę kwadratów: (a + b)(a - b) = a² - b².

Przykład: 2 / (3 + √5)

Mnożymy licznik i mianownik przez (3 - √5), czyli wyrażenie sprzężone do mianownika:

[2 * (3 - √5)] / [(3 + √5) * (3 - √5)] = (6 - 2√5) / (3² - (√5)²) = (6 - 2√5) / (9 - 5) = (6 - 2√5) / 4 = (3 - √5) / 2

Przykłady zadań i ich rozwiązania

Zobaczmy, jak te zasady działają w praktyce, rozwiązując kilka przykładowych zadań.

1. Zadanie: Uprość wyrażenie: 3√8 + √50 - √18 Rozwiązanie:
   • 3√8 = 3√(4 * 2) = 3 * 2√2 = 6√2
   • √50 = √(25 * 2) = 5√2
   • √18 = √(9 * 2) = 3√2
   Zatem: 6√2 + 5√2 - 3√2 = (6 + 5 - 3)√2 = 8√2
2. Zadanie: Oblicz: (√3 + √2)(√3 - √2) Rozwiązanie: Wykorzystujemy wzór na różnicę kwadratów: (a + b)(a - b) = a² - b² Zatem: (√3 + √2)(√3 - √2) = (√3)² - (√2)² = 3 - 2 = 1
3. Zadanie: Usuń niewymierność z mianownika: 4 / √6 Rozwiązanie: Mnożymy licznik i mianownik przez √6: (4 * √6) / (√6 * √6) = 4√6 / 6 = 2√6 / 3

Praktyczne wskazówki i triki

• Zapamiętaj kwadraty i sześciany liczb naturalnych: Ułatwi to wyłączanie czynników przed znak pierwiastka.
• Rozkładaj liczby na czynniki pierwsze: To klucz do upraszczania pierwiastków.
• Zawsze sprawdzaj, czy wynik można jeszcze uprościć: Upewnij się, że wyłączyłeś wszystkie możliwe czynniki przed znak pierwiastka.
• Ćwicz, ćwicz i jeszcze raz ćwicz: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz te zagadnienia.

Podsumowanie

Działania na pierwiastkach mogą wydawać się na początku skomplikowane, ale z pewnością można je opanować, krok po kroku. Pamiętaj o podstawowych definicjach, metodach upraszczania pierwiastków i zasadach wykonywania działań. Upraszczanie wyrażeń z pierwiastkami to niezwykle przydatna umiejętność, która przyda się nie tylko na lekcjach matematyki, ale również w innych dziedzinach nauki. Regularne ćwiczenia i rozwiązywanie zadań sprawią, że poczujesz się pewniej i swobodniej w posługiwaniu się pierwiastkami. Powodzenia!

Mamy nadzieję, że ten artykuł pomógł Ci zrozumieć działania na pierwiastkach. Pamiętaj, że kluczem do sukcesu jest praktyka!