Działania Na Liczbach Naturalnych Klasa 4 Sprawdzian Matematyka Wokół Nas

Drodzy Uczniowie Klasy 4!

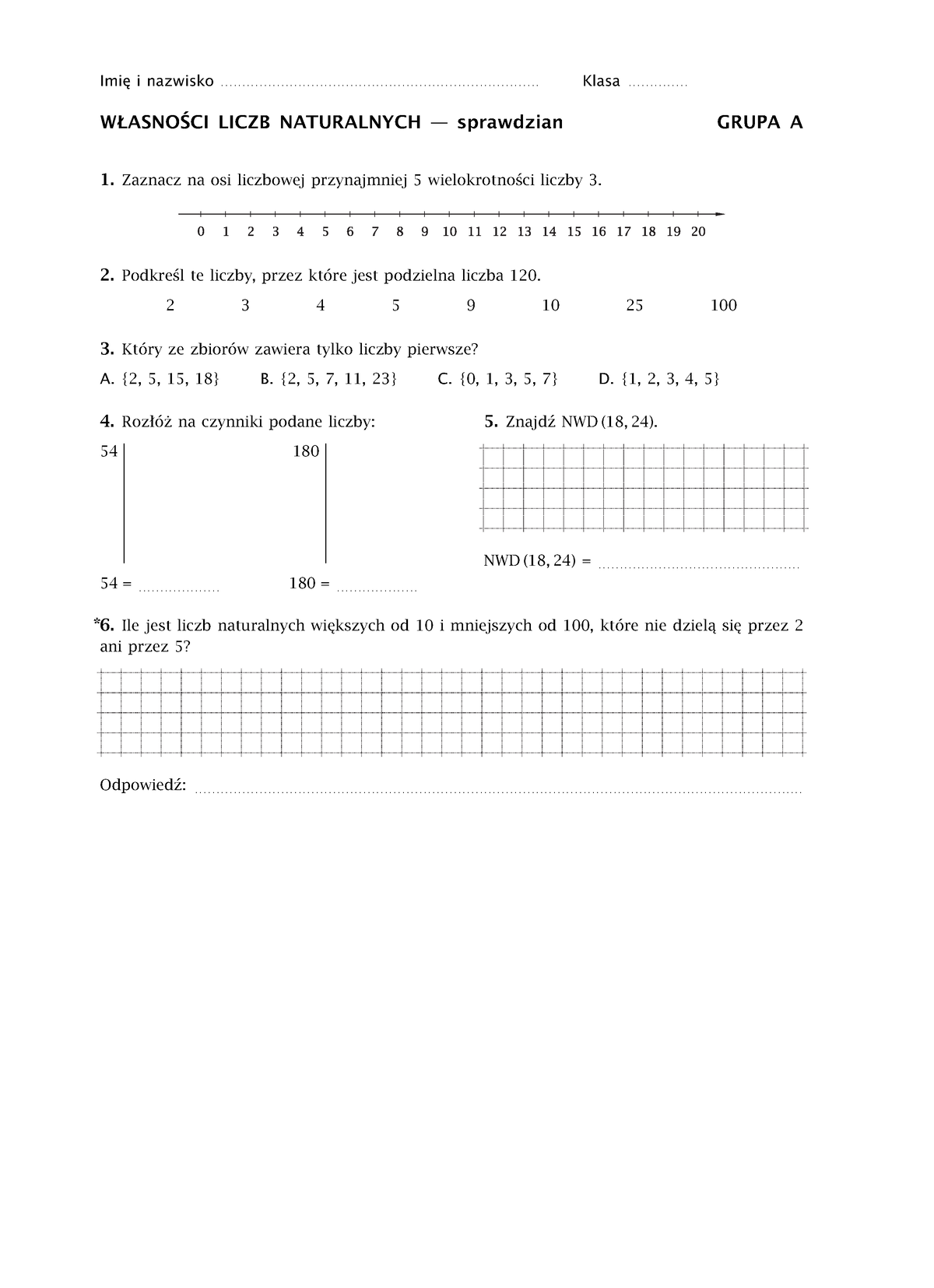
Zauważyłem, że macie pytania dotyczące sprawdzianu z matematyki "Wokół Nas", a konkretnie działu "Działania na Liczbach Naturalnych". Postaram się wam pomóc, prezentując wyczerpujący przegląd zagadnień, które mogą się pojawić. Skupimy się na typowych zadaniach, strategiach rozwiązywania i uwagach dotyczących poprawnego zapisu.

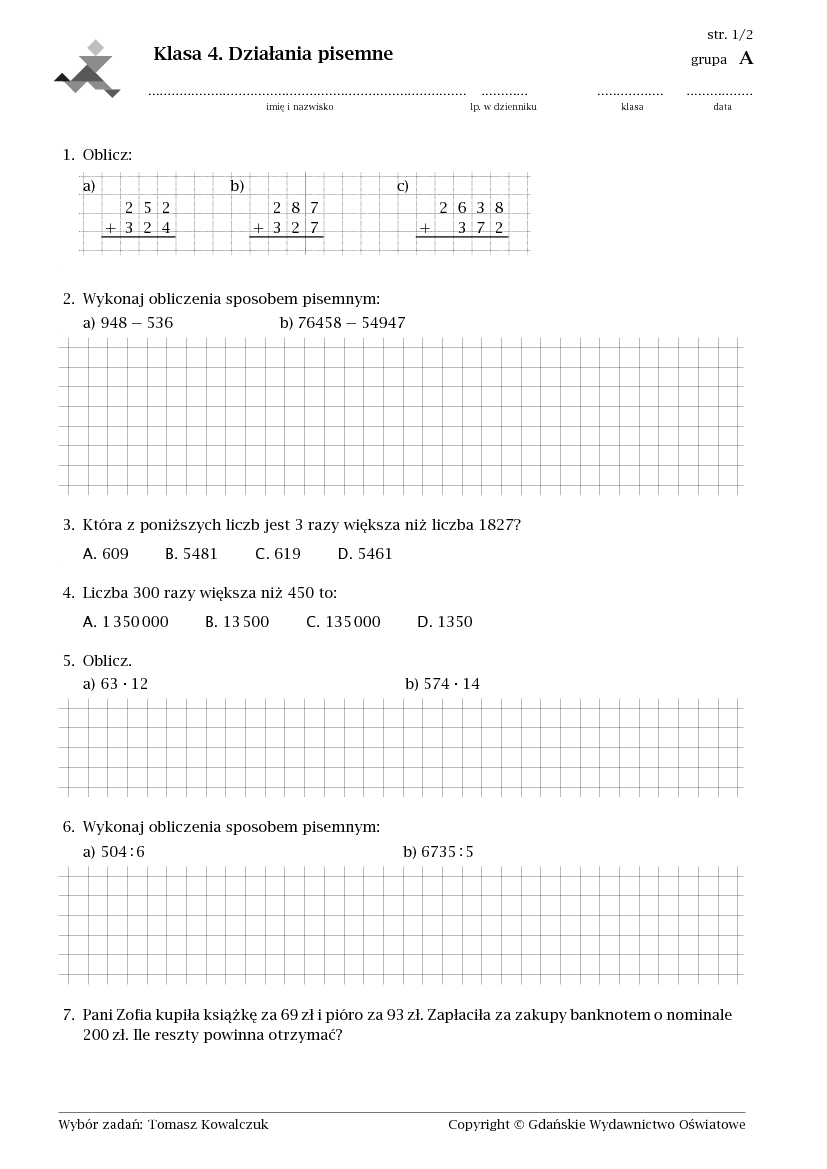
Rozpoczniemy od podstawowych operacji: dodawania, odejmowania, mnożenia i dzielenia. Pamiętajcie, że kluczowa jest znajomość algorytmów pisemnych dla każdej z tych operacji.

Dodawanie Pisemne

W zadaniach z dodawaniem pisemnym, upewnijcie się, że cyfry są ustawione kolumnami – jedności pod jednościami, dziesiątki pod dziesiątkami, setki pod setkami i tak dalej. Następnie dodajcie cyfry w każdej kolumnie, zaczynając od prawej strony (od jedności). Jeśli suma cyfr w kolumnie przekracza 9, zapiszcie cyfrę jedności wyniku, a cyfrę dziesiątek przenieście do następnej kolumny z lewej strony. Przykładowo:

345 + 178 = ?

1. Ustawiamy liczby kolumnami:

   345

   • 178

   ---

2. Dodajemy jedności: 5 + 8 = 13. Zapisujemy 3, a 1 przenosimy do kolumny dziesiątek.

3. Dodajemy dziesiątki (wraz z przeniesioną 1): 4 + 7 + 1 = 12. Zapisujemy 2, a 1 przenosimy do kolumny setek.

4. Dodajemy setki (wraz z przeniesioną 1): 3 + 1 + 1 = 5. Zapisujemy 5.

Ostatecznie: 345 + 178 = 523

Odejmowanie Pisemne

Podobnie jak w dodawaniu, liczby ustawiamy kolumnami. Jeśli cyfra w odjemnej (liczba, od której odejmujemy) jest mniejsza niż cyfra w odjemniku (liczba, którą odejmujemy), musimy "pożyczyć" 1 z kolumny z lewej strony. Pamiętajcie, że pożyczenie 1 z kolumny z lewej strony zmniejsza wartość cyfry w tej kolumnie o 1, a do pożyczonej cyfry dodajemy 10. Przykładowo:

523 - 178 = ?

1. Ustawiamy liczby kolumnami:

   523

   • 178

   ---

2. Odejmujemy jedności: 3 - 8. Nie możemy odjąć 8 od 3, więc pożyczamy 1 z kolumny dziesiątek. Zatem mamy 13 - 8 = 5. Zapisujemy 5.

3. Odejmujemy dziesiątki: Pamiętajmy, że od dwójki w kolumnie dziesiątek pożyczyliśmy 1, więc mamy teraz 1 - 7. Ponownie, nie możemy odjąć 7 od 1, więc pożyczamy 1 z kolumny setek. Zatem mamy 11 - 7 = 4. Zapisujemy 4.

4. Odejmujemy setki: Pamiętajmy, że od piątki w kolumnie setek pożyczyliśmy 1, więc mamy teraz 4 - 1 = 3. Zapisujemy 3.

Ostatecznie: 523 - 178 = 345

Mnożenie Pisemne

Mnożenie pisemne wymaga pomnożenia każdej cyfry jednej liczby przez każdą cyfrę drugiej liczby. Zaczynamy od pomnożenia cyfry jedności drugiej liczby przez każdą cyfrę pierwszej liczby, zapisując wynik pod spodem, zaczynając od prawej strony. Następnie mnożymy cyfrę dziesiątek drugiej liczby przez każdą cyfrę pierwszej liczby, zapisując wynik pod spodem, przesunięty o jedną pozycję w lewo. Kontynuujemy ten proces dla każdej cyfry drugiej liczby. Na koniec, dodajemy wszystkie częściowe wyniki, aby uzyskać ostateczny wynik. Przykładowo:

123 x 45 = ?

1. Mnożymy 123 przez 5 (cyfra jedności w 45):

   123 x 45

   615 (123 x 5)

2. Mnożymy 123 przez 40 (cyfra dziesiątek w 45 pomnożona przez 10): Pamiętajcie o przesunięciu wyniku o jedną pozycję w lewo!

   123 x 45

   615 492 (123 x 4, a następnie dopisujemy 0, ponieważ mnożymy przez 40)

3. Dodajemy częściowe wyniki:

   123 x 45

   615 4920

5535

Ostatecznie: 123 x 45 = 5535

Dzielenie Pisemne

Dzielenie pisemne to proces stopniowego dzielenia dzielnej (liczba dzielona) przez dzielnik (liczba, przez którą dzielimy). Wybieramy fragment dzielnej, który jest większy lub równy dzielnikowi, i dzielimy go. Zapisujemy wynik dzielenia nad dzielną (w ilorazie). Następnie mnożymy iloraz przez dzielnik i odejmujemy wynik od fragmentu dzielnej. Sprowadzamy kolejną cyfrę z dzielnej i powtarzamy proces, aż do momentu, gdy nie będzie już cyfr do sprowadzenia. Przykładowo:

5535 : 45 = ?

1. Sprawdzamy, czy 5 (pierwsza cyfra dzielnej) jest większe lub równe 45 (dzielnik). Nie jest.
2. Sprawdzamy, czy 55 (pierwsze dwie cyfry dzielnej) jest większe lub równe 45. Jest. Dzielimy 55 przez 45. Wynik to 1 (bo 45 mieści się w 55 jeden raz). Zapisujemy 1 nad 55.
3. Mnożymy 1 (iloraz) przez 45 (dzielnik): 1 x 45 = 45. Zapisujemy 45 pod 55 i odejmujemy: 55 - 45 = 10.
4. Sprowadzamy kolejną cyfrę z dzielnej (3). Mamy teraz 103.
5. Dzielimy 103 przez 45. Wynik to 2 (bo 45 mieści się w 103 dwa razy). Zapisujemy 2 nad 3 (obok 1, który już tam jest).
6. Mnożymy 2 (iloraz) przez 45 (dzielnik): 2 x 45 = 90. Zapisujemy 90 pod 103 i odejmujemy: 103 - 90 = 13.
7. Sprowadzamy kolejną cyfrę z dzielnej (5). Mamy teraz 135.
8. Dzielimy 135 przez 45. Wynik to 3 (bo 45 mieści się w 135 trzy razy). Zapisujemy 3 nad 5 (obok 12, które już tam jest).
9. Mnożymy 3 (iloraz) przez 45 (dzielnik): 3 x 45 = 135. Zapisujemy 135 pod 135 i odejmujemy: 135 - 135 = 0. Reszta wynosi 0.

Ostatecznie: 5535 : 45 = 123

Pamiętajcie o sprawdzaniu swoich wyników! Możecie to zrobić mnożąc iloraz przez dzielnik. Wynik powinien być równy dzielnej (lub dzielnej pomniejszonej o resztę, jeśli reszta jest różna od zera).

Kolejność Wykonywania Działań

Bardzo ważne jest, aby znać kolejność wykonywania działań. Pamiętamy o zasadzie:

1. Nawiasy
2. Potęgowanie i Pierwiastkowanie (tego jeszcze nie macie)
3. Mnożenie i Dzielenie (od lewej do prawej)
4. Dodawanie i Odejmowanie (od lewej do prawej)

Przykład:

2 + 3 x 4 = ?

Najpierw wykonujemy mnożenie: 3 x 4 = 12. Następnie wykonujemy dodawanie: 2 + 12 = 14.

Ostatecznie: 2 + 3 x 4 = 14

Jeśli mamy nawiasy, najpierw obliczamy to, co jest w nawiasach:

(2 + 3) x 4 = ?

Najpierw obliczamy to, co jest w nawiasach: 2 + 3 = 5. Następnie wykonujemy mnożenie: 5 x 4 = 20.

Ostatecznie: (2 + 3) x 4 = 20

Zadania Tekstowe

W zadaniach tekstowych kluczowe jest uważne przeczytanie treści i zidentyfikowanie, jakie operacje matematyczne należy wykonać, aby rozwiązać problem. Warto wypisać dane i szukane. Spróbujmy przeanalizować prosty przykład:

"Ania ma 15 jabłek, a Kasia ma 8 jabłek więcej niż Ania. Ile jabłek mają razem?"

1. Dane:

   • Ania: 15 jabłek
   • Kasia: 8 jabłek więcej niż Ania

2. Szukane:

   • Ile jabłek mają razem?

3. Rozwiązanie:

   • Najpierw obliczamy, ile jabłek ma Kasia: 15 + 8 = 23 jabłka
   • Następnie obliczamy, ile jabłek mają razem: 15 + 23 = 38 jabłek

4. Odpowiedź: Ania i Kasia mają razem 38 jabłek.

Kluczowe jest zrozumienie, że "więcej niż" oznacza dodawanie, "mniej niż" oznacza odejmowanie, "razy" oznacza mnożenie, a "podzielić na równe części" oznacza dzielenie. Często pomocne jest narysowanie schematu lub diagramu, aby lepiej zrozumieć relacje między danymi w zadaniu.

Pamiętajcie również o jednostkach! Jeśli w zadaniu występują różne jednostki (np. metry i centymetry), najpierw należy je zamienić na jedną jednostkę.

Mam nadzieję, że to kompendium pomoże Wam w przygotowaniu się do sprawdzianu! Powodzenia!