Działania Na Liczbach Klasa 8

Czy liczby to dla Ciebie tylko zbiór symboli, czy fascynujący świat pełen zagadek i możliwości? W klasie 8 wkraczamy na nowy poziom zrozumienia działań na liczbach. Ten artykuł jest Twoim przewodnikiem po tym zagadnieniu, niezależnie od tego, czy jesteś matematycznym orłem, czy dopiero zaczynasz swoją przygodę z liczbami. Razem przejdziemy przez podstawy, poszerzymy wiedzę i nauczymy się, jak wykorzystywać matematykę w praktyce.

Dlaczego działania na liczbach są ważne?

Może wydawać się, że działania na liczbach to tylko sucha teoria, ale w rzeczywistości towarzyszą nam one na każdym kroku. Pomyśl o planowaniu budżetu, gotowaniu według przepisów, obliczaniu odległości podczas podróży – wszędzie tam wykorzystujesz podstawowe operacje matematyczne. Zrozumienie tych zasad otwiera drzwi do rozwiązywania rzeczywistych problemów i ułatwia naukę innych przedmiotów, takich jak fizyka czy chemia.

Dodatkowo, solidne podstawy w działaniach na liczbach to fundament dla dalszej edukacji matematycznej. Bez tego trudno będzie zrozumieć algebrę, geometrię czy analizę matematyczną.

Podstawowe działania: Przypomnienie i utrwalenie

Zacznijmy od przypomnienia podstawowych operacji, które znasz już od dawna. Utrwalenie tych wiadomości to klucz do sukcesu w dalszych, bardziej skomplikowanych obliczeniach.

Dodawanie i odejmowanie

Dodawanie to łączenie dwóch lub więcej liczb w jedną sumę. Odejmowanie to proces odwrotny, czyli znajdowanie różnicy między dwiema liczbami. Pamiętaj o:

Znakach liczb: Liczba dodatnia (+) i liczba ujemna (-). Zwróć szczególną uwagę na odejmowanie liczb ujemnych, np. 5 - (-3) = 5 + 3 = 8.
Kolejności wykonywania działań: Zaczynamy od lewej do prawej, chyba że występują nawiasy.

Przykład: 7 + (-2) - 5 = 5 - 5 = 0

Mnożenie i dzielenie

Mnożenie to powtarzane dodawanie tej samej liczby. Dzielenie to rozdzielanie jednej liczby na równe części. Ważne zasady:

Znak iloczynu/ilorazu:
- (+) * (+) = (+)
- (+) * (-) = (-)
- (-) * (+) = (-)
- (-) * (-) = (+)
Dzielenie przez zero: Jest niedozwolone!

Przykład: (-3) * 4 / (-2) = -12 / (-2) = 6

Potęgowanie i pierwiastkowanie

Potęgowanie to skrócony zapis mnożenia tej samej liczby przez samą siebie. Pierwiastkowanie to proces odwrotny – szukanie liczby, która podniesiona do danej potęgi da wynik.

Potęgowanie

Liczba podnoszona do potęgi to podstawa potęgi, a liczba wskazująca, ile razy mnożymy podstawę przez siebie to wykładnik potęgi. Na przykład, 2³ = 2 * 2 * 2 = 8.

Potęga o wykładniku 0: Dowolna liczba (różna od zera) podniesiona do potęgi 0 daje 1. (a⁰ = 1, dla a ≠ 0)
Potęga o wykładniku 1: Dowolna liczba podniesiona do potęgi 1 daje samą siebie. (a¹ = a)
Potęgi liczb ujemnych: Znak wyniku zależy od wykładnika. Jeśli wykładnik jest parzysty, wynik jest dodatni. Jeśli wykładnik jest nieparzysty, wynik jest ujemny. (np. (-2)² = 4, ale (-2)³ = -8)

Pierwiastkowanie

Pierwiastek kwadratowy z liczby to liczba, która pomnożona przez samą siebie daje daną liczbę. Na przykład, √9 = 3, ponieważ 3 * 3 = 9. Ogólnie, ⁿ√a = b, jeśli bⁿ = a.

Pierwiastek z liczby ujemnej: W zbiorze liczb rzeczywistych nie istnieje pierwiastek kwadratowy z liczby ujemnej.
Pierwiastek z zera: √0 = 0

Pamiętaj! Potęgowanie i pierwiastkowanie są działaniami odwrotnymi.

Kolejność wykonywania działań

Aby uniknąć błędów w obliczeniach, musimy przestrzegać kolejności wykonywania działań. Ułatwi nam to zapamiętanie akronimu: Kolejność Działań: Nawiasy, Potęgowanie/Pierwiastkowanie, Mnożenie/Dzielenie, Dodawanie/Odejmowanie (czasami zapamiętywane jako: Nawiasy, Potęgi, Mnożenie i Dzielenie, Dodawanie i Odejmowanie – NDPDiO). Czyli:

Nawiasy: Najpierw wykonujemy działania w nawiasach, zaczynając od nawiasów najbardziej wewnętrznych.
Potęgowanie i pierwiastkowanie: Następnie obliczamy potęgi i pierwiastki.
Mnożenie i dzielenie: Kolejno wykonujemy mnożenie i dzielenie, od lewej do prawej.
Dodawanie i odejmowanie: Na końcu wykonujemy dodawanie i odejmowanie, również od lewej do prawej.

Przykład: 2 + 3 * (4 - 1)² = 2 + 3 * 3² = 2 + 3 * 9 = 2 + 27 = 29

Działania na ułamkach zwykłych i dziesiętnych

Ułamki zwykłe (np. ½, ¾) i ułamki dziesiętne (np. 0,5, 0,75) to liczby, które reprezentują części całości. Musimy umieć wykonywać na nich wszystkie podstawowe działania.

Działania na ułamkach zwykłych

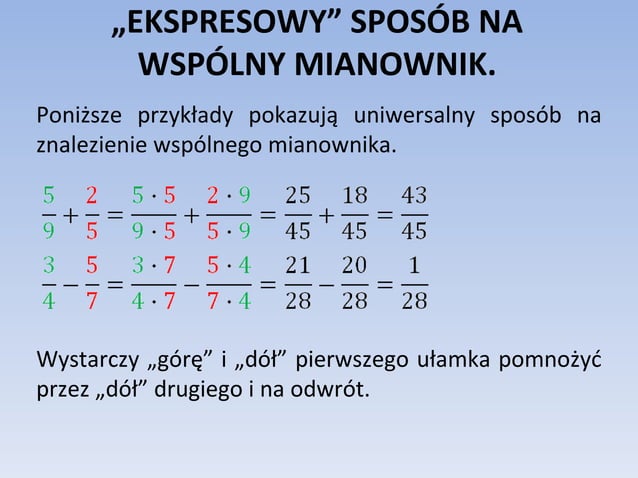
Dodawanie i odejmowanie: Ułamki muszą mieć wspólny mianownik. Następnie dodajemy lub odejmujemy liczniki, a mianownik pozostaje bez zmian.
Mnożenie: Mnożymy licznik przez licznik i mianownik przez mianownik.
Dzielenie: Dzielenie to mnożenie przez odwrotność drugiego ułamka.

Przykład: ½ + ¼ = 2/4 + 1/4 = ¾, ½ * ¼ = 1/8, ½ / ¼ = ½ * 4/1 = 2

Działania na ułamkach dziesiętnych

Dodawanie i odejmowanie: Ustawiamy ułamki tak, aby przecinek był pod przecinkiem, a następnie dodajemy lub odejmujemy jak liczby całkowite.
Mnożenie: Mnożymy jak liczby całkowite, a następnie przesuwamy przecinek w wyniku o tyle miejsc w lewo, ile wynosi suma miejsc po przecinku w obu mnożonych liczbach.
Dzielenie: Przesuwamy przecinek w dzielniku i dzielnej o tyle miejsc w prawo, aby dzielnik stał się liczbą całkowitą, a następnie wykonujemy dzielenie.

Przykład: 0,5 + 0,25 = 0,75, 0,5 * 0,25 = 0,125, 0,5 / 0,25 = 2

Działania na liczbach wymiernych i niewymiernych

Liczby wymierne to liczby, które można zapisać w postaci ułamka zwykłego (np. 2, -3, 0,5). Liczby niewymierne to liczby, których nie można zapisać w postaci ułamka zwykłego (np. √2, π).

Działania na liczbach wymiernych są podobne do działań na ułamkach zwykłych i dziesiętnych. Natomiast działania na liczbach niewymiernych często wymagają użycia kalkulatora lub przybliżeń.

Pamiętaj! Wynik dodawania, odejmowania, mnożenia lub dzielenia liczby wymiernej i niewymiernej jest zawsze liczbą niewymierną (z wyjątkiem mnożenia lub dzielenia przez zero).

Praktyczne zastosowania: Przykłady z życia wzięte

Spójrzmy na kilka przykładów, jak wiedza o działaniach na liczbach przydaje się w codziennym życiu:

Planowanie budżetu: Obliczanie wydatków i oszczędności.
Gotowanie: Przeliczanie proporcji składników w przepisach.
Zakupy: Obliczanie rabatów i porównywanie cen.
Podróże: Obliczanie odległości i czasu podróży.
Inwestycje: Obliczanie procentów i zysków.

Im lepiej opanujesz działania na liczbach, tym łatwiej będzie Ci radzić sobie z różnymi sytuacjami w życiu codziennym.

Wskazówki i triki

Oto kilka dodatkowych wskazówek, które pomogą Ci w nauce działań na liczbach:

Ćwicz regularnie: Im więcej ćwiczysz, tym lepiej utrwalisz wiedzę.
Używaj kalkulatora: Kalkulator może być pomocny przy sprawdzaniu wyników i wykonywaniu skomplikowanych obliczeń.
Szukaj pomocy: Jeśli masz trudności, nie wstydź się pytać nauczyciela, rodziców lub kolegów.
Graj w gry matematyczne: Gry matematyczne to świetny sposób na naukę przez zabawę.
Wykorzystuj matematykę w praktyce: Szukaj okazji do wykorzystywania wiedzy matematycznej w życiu codziennym.

Zrozumienie i umiejętność wykonywania działań na liczbach to kluczowa umiejętność, która przyda Ci się w szkole, w życiu zawodowym i osobistym. Nie zrażaj się trudnościami, ćwicz regularnie i ciesz się odkrywaniem fascynującego świata liczb!