Działania Na Liczbach Klasa 5

Czy liczby sprawiają Ci czasem trudności? Rozumiem! Dla wielu uczniów, szczególnie w 5 klasie, działania na liczbach mogą wydawać się skomplikowane. Ale nie martw się! Razem spróbujemy to uprościć i sprawić, że matematyka stanie się bardziej zrozumiała i przyjemna.

Podstawowe Działania: Fundament Matematyki

Zacznijmy od podstaw, czyli od dodawania, odejmowania, mnożenia i dzielenia. To one są fundamentem, na którym buduje się cała reszta. Ważne jest, by dobrze je opanować.

Dodawanie i Odejmowanie

Dodawanie to nic innego jak łączenie dwóch lub więcej liczb w jedną sumę. Wyobraź sobie, że masz 3 jabłka, a Twój kolega daje Ci jeszcze 2. Ile masz razem? 3 + 2 = 5 jabłek!

Odejmowanie to natomiast zabieranie czegoś. Jeśli miałeś 5 jabłek i zjadłeś 1, to ile Ci zostało? 5 - 1 = 4 jabłka.

Pamiętaj o kilku ważnych zasadach:

Kolejność wykonywania działań: W działaniach bez nawiasów, dodawanie i odejmowanie wykonujemy od lewej do prawej.
Liczby ujemne: Na początku mogą wydawać się dziwne, ale pomyśl o długu. Jeśli masz -3 zł, to znaczy, że jesteś komuś winien 3 zł.

Mnożenie i Dzielenie

Mnożenie to skrócone dodawanie. Jeśli masz 3 grupy po 4 cukierki w każdej, to ile masz cukierków razem? Możesz dodać 4 + 4 + 4 = 12, ale prościej jest pomnożyć 3 x 4 = 12.

Dzielenie to rozdzielanie czegoś na równe części. Jeśli masz 12 cukierków i chcesz je rozdać równo pomiędzy 3 osoby, to ile cukierków dostanie każda osoba? 12 : 3 = 4 cukierki.

Kilka ważnych wskazówek:

Tabliczka mnożenia: Naucz się jej na pamięć! To bardzo ułatwi Ci rozwiązywanie zadań.
Dzielenie przez zero: Pamiętaj, że nie można dzielić przez zero! To niedozwolone działanie w matematyce.

Kolejność Wykonywania Działań: Klucz do Sukcesu

To bardzo ważny temat! Kiedy w jednym działaniu występuje kilka różnych operacji, musimy wiedzieć, w jakiej kolejności je wykonywać, żeby otrzymać poprawny wynik. Wyobraź sobie, że masz do policzenia: 2 + 3 x 4. Co robisz najpierw?

Kolejność jest następująca:

Nawiasy: Jeśli w działaniu są nawiasy, najpierw wykonujemy działania w nawiasach.
Potęgowanie i pierwiastkowanie: Tego w 5 klasie jeszcze nie ma, ale warto wiedzieć na przyszłość.
Mnożenie i dzielenie: Wykonujemy od lewej do prawej.
Dodawanie i odejmowanie: Wykonujemy od lewej do prawej.

W przykładzie 2 + 3 x 4 najpierw wykonujemy mnożenie: 3 x 4 = 12, a dopiero potem dodajemy: 2 + 12 = 14. Gdybyśmy dodali najpierw, otrzymalibyśmy zły wynik!

Ułamki: Nie Taki Diabeł Straszny

Ułamki często budzą niepokój, ale wcale nie są takie trudne. Ułamek to po prostu część całości. Na przykład, jeśli podzielisz pizzę na 8 kawałków i zjesz 3 z nich, to zjadłeś 3/8 pizzy.

Budowa ułamka:

Licznik: To liczba na górze ułamka, która mówi, ile części mamy.
Mianownik: To liczba na dole ułamka, która mówi, na ile części podzielona jest całość.

Działania na ułamkach

Dodawanie i odejmowanie ułamków o tych samych mianownikach: To proste! Wystarczy dodać lub odjąć liczniki, a mianownik zostaje ten sam. Na przykład: 2/5 + 1/5 = 3/5.

Mnożenie ułamków: Mnożymy licznik przez licznik i mianownik przez mianownik. Na przykład: 1/2 x 2/3 = 2/6.

Dzielenie ułamków: Dzielenie ułamków to mnożenie przez odwrotność drugiego ułamka. Na przykład: 1/2 : 2/3 = 1/2 x 3/2 = 3/4.

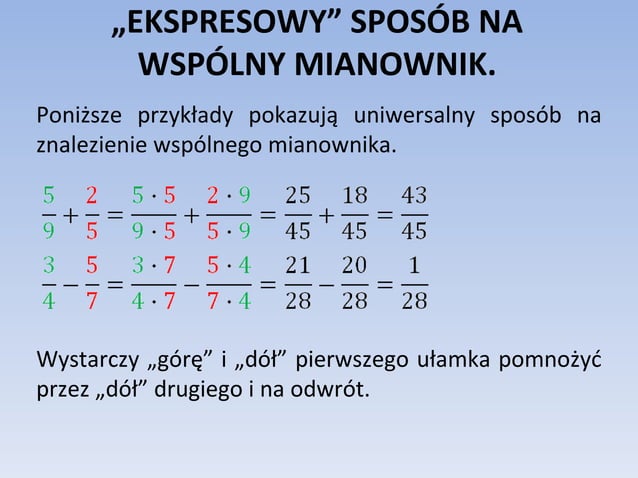
Sprowadzanie ułamków do wspólnego mianownika: To ważne, gdy chcemy dodać lub odjąć ułamki o różnych mianownikach. Znajdujemy najmniejszą wspólną wielokrotność (NWW) mianowników i sprowadzamy ułamki do tego mianownika.

Liczby Dziesiętne: Alternatywny Zapis

Liczby dziesiętne to inny sposób zapisu ułamków. Mają przecinek, który oddziela część całkowitą od części ułamkowej. Na przykład: 3,5 to trzy całe i pięć dziesiątych.

Działania na liczbach dziesiętnych

Dodawanie i odejmowanie: Ważne jest, aby wyrównać przecinki. Dopisz zera, aby liczby miały tyle samo miejsc po przecinku, a następnie dodaj lub odejmij jak zwykłe liczby.

Mnożenie: Mnożymy jak zwykłe liczby, a na końcu liczymy, ile miejsc po przecinku mają łącznie obie liczby i odliczamy tyle samo miejsc w wyniku.

Dzielenie: Jeśli dzielnik jest liczbą dziesiętną, przesuwamy przecinek w dzielniku i dzielnej o tyle samo miejsc, aby dzielnik stał się liczbą całkowitą, a następnie dzielimy jak zwykłe liczby.

Zadania Tekstowe: Matematyka w Praktyce

Zadania tekstowe sprawiają trudność, bo trzeba zrozumieć, o co pytają i jakie działania wykonać. Ale to właśnie one pokazują, jak matematyka przydaje się w życiu!

Jak rozwiązywać zadania tekstowe?

Przeczytaj uważnie: Zrozum treść zadania. Co wiesz? O co pytają?
Wypisz dane: Zapisz wszystkie liczby i informacje z zadania.
Zaplanuj rozwiązanie: Zastanów się, jakie działania musisz wykonać, aby odpowiedzieć na pytanie.
Wykonaj obliczenia: Oblicz to, co zaplanowałeś.
Sprawdź odpowiedź: Czy Twoja odpowiedź ma sens? Czy pasuje do treści zadania?

Przykład: Ania ma 15 cukierków. Dała Kasi 5 cukierków, a potem kupiła jeszcze 7. Ile cukierków ma teraz Ania?

Rozwiązanie:

Ania miała 15 cukierków.
Dała Kasi 5, więc ma 15 - 5 = 10 cukierków.
Kupiła jeszcze 7, więc ma 10 + 7 = 17 cukierków.
Odpowiedź: Ania ma teraz 17 cukierków.

Praktyczne Wskazówki i Triki

Oto kilka dodatkowych wskazówek, które mogą Ci pomóc:

Ćwicz regularnie: Im więcej ćwiczysz, tym lepiej rozumiesz matematykę.
Używaj materiałów pomocniczych: Skorzystaj z podręczników, zeszytów ćwiczeń, filmów edukacyjnych i gier online.
Szukaj pomocy: Jeśli masz trudności, poproś o pomoc nauczyciela, rodzica, starszego brata lub siostrę, albo kolegę z klasy.
Baw się matematyką: Matematyka może być zabawna! Szukaj gier i zadań, które Cię interesują.
Wykorzystuj matematykę w życiu codziennym: Obliczaj ceny w sklepie, planuj budżet, mierz odległości – to pomoże Ci zrozumieć, jak matematyka jest ważna.

Pamiętaj, że każdy uczy się w swoim tempie. Nie zrażaj się trudnościami, bądź cierpliwy i wytrwały, a na pewno osiągniesz sukces! Powodzenia!