Dwa Okręgi Są Styczne Wewnętrznie Odległość Między Ich środkami Wynosi

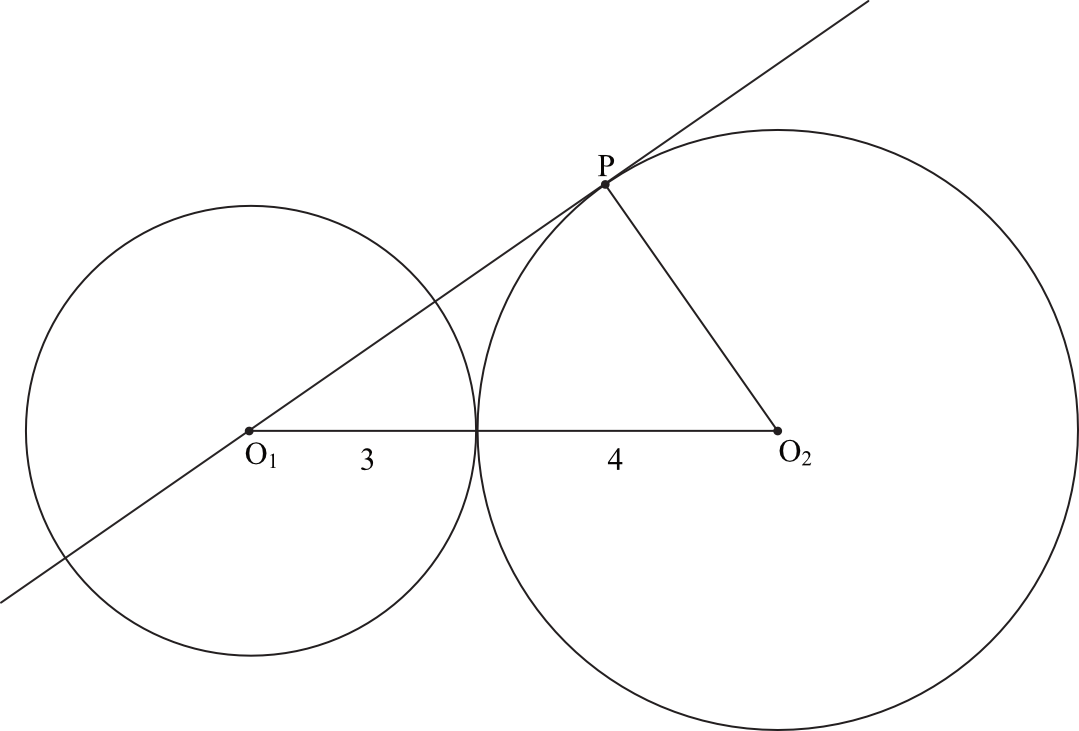
Drodzy Uczniowie,

Otrzymałem Wasze pytania dotyczące sytuacji, w której dwa okręgi są styczne wewnętrznie, a znana jest odległość między ich środkami. Postaram się przedstawić Wam kompleksowe omówienie tego zagadnienia, bazując na mojej wiedzy i doświadczeniu.

Kluczowe w zrozumieniu tego problemu jest precyzyjne zdefiniowanie, co oznacza styczność wewnętrzna okręgów. Dwa okręgi są styczne wewnętrznie, gdy jeden z nich znajduje się wewnątrz drugiego i mają dokładnie jeden punkt wspólny. Ten punkt wspólny nazywamy punktem styczności. Co istotne, zarówno środki okręgów, jak i punkt styczności leżą na jednej prostej.

Rozważmy dwa okręgi: okrąg O₁ o promieniu r₁ i okrąg O₂ o promieniu r₂. Załóżmy, że okrąg O₂ leży wewnątrz okręgu O₁ i są one styczne wewnętrznie. Oznaczmy odległość między środkami tych okręgów jako d. Naszym celem jest wyrażenie tej odległości d w zależności od promieni r₁ i r₂.

Możemy rozważyć dwa przypadki:

r₁ > r₂: W tym przypadku okrąg O₂ jest mniejszy i leży wewnątrz okręgu O₁. Odległość między środkami okręgów d jest równa różnicy promieni: d = r₁ - r₂. To dlatego, że odległość od środka O₁ do punktu styczności jest równa r₁, a odległość od środka O₂ do punktu styczności jest równa r₂. Ponieważ wszystkie trzy punkty (O₁, O₂ i punkt styczności) leżą na jednej prostej, odległość między O₁ i O₂ musi być różnicą promieni.
r₂ > r₁: W tym przypadku okrąg O₁ jest mniejszy i leży wewnątrz okręgu O₂. Analogicznie, odległość między środkami okręgów d jest równa różnicy promieni: d = r₂ - r₁.

W obu przypadkach, odległość między środkami dwóch okręgów stycznych wewnętrznie jest równa wartości bezwzględnej różnicy ich promieni. Możemy to zapisać jako: d = |r₁ - r₂|. Jest to fundamentalna relacja, którą musimy zapamiętać.

Teraz przejdźmy do zastosowań tej wiedzy w rozwiązywaniu konkretnych problemów.

Zadanie 1:

Dane są dwa okręgi styczne wewnętrznie. Promień większego okręgu wynosi 10 cm, a odległość między środkami okręgów wynosi 4 cm. Oblicz promień mniejszego okręgu.

Rozwiązanie:

Oznaczmy promień większego okręgu jako r₁ = 10 cm, a promień mniejszego okręgu jako r₂. Odległość między środkami okręgów wynosi d = 4 cm. Zgodnie z naszym wzorem:

d = |r₁ - r₂|

4 = |10 - r₂|

Rozważamy dwa przypadki:

10 - r₂ = 4 => r₂ = 10 - 4 = 6 cm
10 - r₂ = -4 => r₂ = 10 + 4 = 14 cm

Ponieważ r₂ musi być mniejsze od r₁, to jedynym poprawnym rozwiązaniem jest r₂ = 6 cm.

Zadanie 2:

Dwa okręgi są styczne wewnętrznie. Promień jednego z okręgów wynosi 5 cm. Odległość między środkami okręgów wynosi 2 cm. Jakie mogą być promienie drugiego okręgu?

Rozwiązanie:

Oznaczmy promień jednego okręgu jako r₁ = 5 cm. Niech r₂ będzie promieniem drugiego okręgu. Odległość między środkami okręgów wynosi d = 2 cm. Znowu korzystamy ze wzoru:

d = |r₁ - r₂|

2 = |5 - r₂|

Rozważamy dwa przypadki:

5 - r₂ = 2 => r₂ = 5 - 2 = 3 cm
5 - r₂ = -2 => r₂ = 5 + 2 = 7 cm

W tym przypadku, oba rozwiązania są poprawne. Promień drugiego okręgu może wynosić 3 cm lub 7 cm. Jeśli r₂ = 3 cm, to okrąg o promieniu 3 cm jest mniejszy i leży wewnątrz okręgu o promieniu 5 cm. Jeśli r₂ = 7 cm, to okrąg o promieniu 5 cm jest mniejszy i leży wewnątrz okręgu o promieniu 7 cm.

Złożone Konfiguracje i Dodatkowe Wskazówki

Styczność wewnętrzna okręgów może być elementem bardziej skomplikowanych konfiguracji geometrycznych. Na przykład, możemy mieć trójkąt, w który wpisany jest okrąg, a następnie drugi okrąg styczny wewnętrznie do tego okręgu i do boków trójkąta. Analiza takich problemów wymaga często zastosowania dodatkowych narzędzi, takich jak twierdzenie Pitagorasa, trygonometria, czy właściwości podobieństwa figur.

Ważnym elementem jest także umiejętność rysowania precyzyjnych diagramów. Dobry rysunek często pozwala na wizualizację problemu i ułatwia znalezienie poprawnego rozwiązania. Pamiętajcie, aby zaznaczać na rysunku wszystkie istotne dane, takie jak promienie okręgów, odległości między środkami, punkty styczności, itp.

Kolejna ważna wskazówka to uważne czytanie treści zadania. Często w zadaniach podawane są dodatkowe informacje, które mogą okazać się kluczowe w rozwiązaniu. Na przykład, możemy mieć podany kąt między promieniem jednego okręgu a prostą przechodzącą przez środek drugiego okręgu. Wykorzystanie takich informacji pozwala na zbudowanie odpowiednich równań i rozwiązanie problemu.

Przykłady Zastosowań w Geometrii Analitycznej

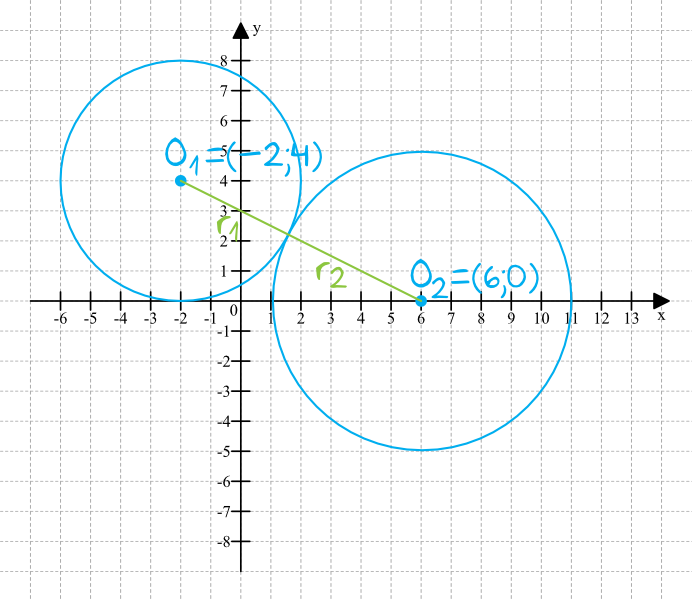
Styczność wewnętrzna okręgów znajduje również zastosowanie w geometrii analitycznej. Jeżeli mamy dane równania dwóch okręgów, możemy sprawdzić, czy są one styczne wewnętrznie, analizując odległość między ich środkami oraz porównując ją z różnicą ich promieni.

Równanie okręgu o środku w punkcie (a, b) i promieniu r ma postać: (x - a)² + (y - b)² = r². Jeżeli mamy dwa okręgi o równaniach:

(x - a₁)² + (y - b₁)² = r₁²
(x - a₂)² + (y - b₂)² = r₂²

to odległość między ich środkami wynosi: d = √((a₂ - a₁)² + (b₂ - b₁)²).

Aby okręgi były styczne wewnętrznie, musi być spełniony warunek: d = |r₁ - r₂|. Sprawdzenie tego warunku pozwala na stwierdzenie, czy okręgi są styczne wewnętrznie, czy też nie.

Podsumowując, zrozumienie koncepcji styczności wewnętrznej okręgów jest kluczowe dla rozwiązywania wielu problemów geometrycznych. Mam nadzieję, że moje wyjaśnienia były dla Was pomocne. W razie dodatkowych pytań, jestem do Waszej dyspozycji. Pamiętajcie o ćwiczeniach i rozwiązywaniu zadań, aby utrwalić zdobytą wiedzę. Powodzenia!