Dwa Graniastoslupy Proste Czworokatne Maja Taka Sama Wysokosc Rowna 5

Dobrze, rozważmy więc dwa graniastosłupy proste czworokątne, oba o wysokości równej 5. Spróbujmy przeanalizować różne aspekty związane z takimi graniastosłupami, uwzględniając ich pola powierzchni, objętości oraz możliwe konfiguracje podstaw.

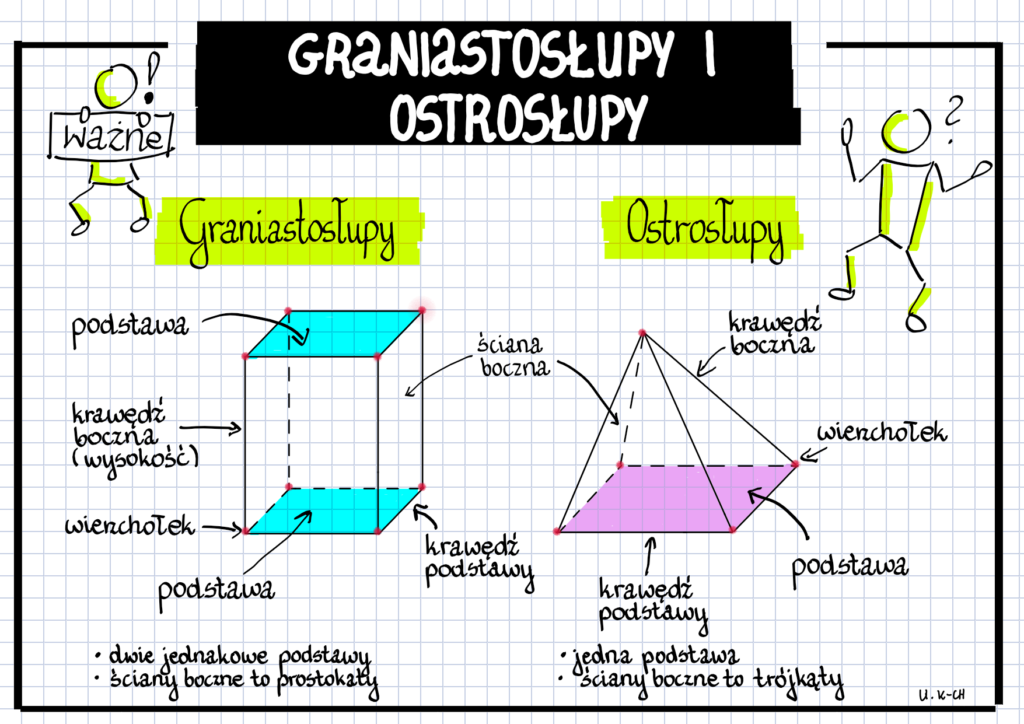
Graniastosłup prosty czworokątny to bryła, której podstawą jest czworokąt, a ściany boczne są prostokątami prostopadłymi do podstawy. "Prosty" oznacza, że krawędzie boczne są prostopadłe do płaszczyzn podstaw. "Czworokątny" precyzuje, że podstawa jest czworokątem, który może być kwadratem, prostokątem, równoległobokiem, trapezem, deltoidem lub dowolnym innym czworobokiem.

Skoro oba graniastosłupy mają tę samą wysokość równą 5, to różnice w ich właściwościach (np. objętości, polu powierzchni) będą wynikały wyłącznie z różnic w kształcie i wymiarach ich podstaw.

Zacznijmy od objętości. Objętość graniastosłupa obliczamy jako iloczyn pola podstawy i wysokości: V = Pp * h. Ponieważ h = 5 dla obu graniastosłupów, ich objętości będą równe wtedy i tylko wtedy, gdy pola ich podstaw będą równe. Oznacza to, że mimo iż czworokąty w podstawie mogą wyglądać zupełnie inaczej, muszą mieć identyczne pola powierzchni, aby objętości graniastosłupów były takie same. Na przykład, jeden graniastosłup może mieć w podstawie prostokąt o wymiarach 2 x 3, co daje pole 6, a drugi może mieć trapez o wysokości 2 i podstawach długości 2 i 4 (pole trapezu to (a+b)*h/2 = (2+4)*2/2 = 6). Mimo różnic w kształcie podstaw, objętości graniastosłupów będą identyczne, wynoszące 6 * 5 = 30.

Przejdźmy teraz do pola powierzchni. Pole powierzchni całkowitej graniastosłupa to suma pól dwóch podstaw i pola powierzchni bocznej: Pc = 2Pp + Pb. Pole powierzchni bocznej obliczamy jako sumę pól wszystkich ścian bocznych, które w przypadku graniastosłupa prostego są prostokątami. Pole powierzchni bocznej można również obliczyć jako iloczyn obwodu podstawy i wysokości graniastosłupa: Pb = Obwód_podstawy * h.

Zauważmy, że nawet jeśli pola podstaw obu graniastosłupów są równe, ich pola powierzchni całkowitej mogą być różne. Wynika to z faktu, że obwody podstaw mogą być różne, nawet jeśli pola są identyczne. Wróćmy do przykładu z prostokątem 2 x 3 i trapezem. Prostokąt ma obwód 2(2+3) = 10. Obwód trapezu zależy od długości jego ramion. Załóżmy, że trapez jest równoramienny, a każde z ramion ma długość sqrt(1^2 + 2^2) = sqrt(5) (korzystamy z twierdzenia Pitagorasa, zakładając, że ramię tworzy trójkąt prostokątny o wysokości 2 i podstawie 1, ponieważ podstawa trapezu o długości 4 jest o 2 dłuższa niż podstawa o długości 2, a ta różnica jest równomiernie rozłożona na oba boki). Wtedy obwód trapezu wynosi 2 + 4 + 2*sqrt(5) = 6 + 2*sqrt(5) ≈ 10.47. Widać, że obwody są różne. Zatem, pole powierzchni bocznej prostokątnego graniastosłupa będzie wynosić 10 * 5 = 50, a pole powierzchni bocznej graniastosłupa o podstawie trapezoidalnej wyniesie (6 + 2*sqrt(5)) * 5 = 30 + 10*sqrt(5) ≈ 52.36. W rezultacie, pole powierzchni całkowitej graniastosłupa o podstawie prostokątnej wyniesie 2 * 6 + 50 = 62, a pole powierzchni całkowitej graniastosłupa o podstawie trapezoidalnej wyniesie 2 * 6 + 30 + 10*sqrt(5) = 42 + 10*sqrt(5) ≈ 64.36.

Analiza różnych typów czworokątów jako podstaw graniastosłupów:

Kwadrat: Jeśli podstawa jest kwadratem o boku a, to pole podstawy wynosi a^2, obwód wynosi 4a, objętość graniastosłupa to a^2 * 5, a pole powierzchni całkowitej to 2a^2 + 4a * 5 = 2a^2 + 20a.

Prostokąt: Jeśli podstawa jest prostokątem o bokach a i b, to pole podstawy wynosi a * b, obwód wynosi 2(a+b), objętość graniastosłupa to a * b * 5, a pole powierzchni całkowitej to 2ab + 2(a+b) * 5 = 2ab + 10a + 10b.

Równoległobok: Jeśli podstawa jest równoległobokiem o bokach a i b oraz kącie ostrym α między nimi, to pole podstawy wynosi a * b * sin(α), obwód wynosi 2(a+b), objętość graniastosłupa to a * b * sin(α) * 5, a pole powierzchni całkowitej to 2ab*sin(α) + 2(a+b) * 5 = 2ab*sin(α) + 10a + 10b.

Trapez: Jeśli podstawa jest trapezem o podstawach a i b oraz wysokości h_t, to pole podstawy wynosi (a+b) * h_t / 2, obwód zależy od długości ramion (c i d), objętość graniastosłupa to (a+b) * h_t / 2 * 5, a pole powierzchni całkowitej to 2 * (a+b) * h_t / 2 + (a + b + c + d) * 5.

Deltoid: Jeśli podstawa jest deltoidem o przekątnych e i f, to pole podstawy wynosi e * f / 2, obwód zależy od długości boków (dwa boki o długości a i dwa o długości b), objętość graniastosłupa to e * f / 2 * 5, a pole powierzchni całkowitej to 2 * e * f / 2 + (2a + 2b) * 5 = ef + 10a + 10b.

H2 Zależności między parametrami

Podsumowując, posiadając dwa graniastosłupy proste czworokątne o tej samej wysokości, możemy wywnioskować następujące zależności:

Równość objętości: Aby objętości graniastosłupów były równe, pola ich podstaw muszą być identyczne. Kształt podstaw nie ma znaczenia, liczy się jedynie pole powierzchni.
Różnice w polu powierzchni: Nawet jeśli pola podstaw są równe, pola powierzchni całkowitej mogą się różnić. Wynika to z różnic w obwodach podstaw. Im większy obwód podstawy, tym większe pole powierzchni bocznej, a w konsekwencji - większe pole powierzchni całkowitej.
Wpływ kształtu podstawy: Różne kształty czworokątów (kwadrat, prostokąt, równoległobok, trapez, deltoid) prowadzą do różnych wzorów na obliczanie pola podstawy i obwodu, co z kolei wpływa na objętość i pole powierzchni całkowitej graniastosłupa.

H2 Specjalne przypadki i konfiguracje

Rozważmy kilka szczególnych przypadków:

Dwa graniastosłupy o podstawach będących kwadratami: Jeśli oba graniastosłupy mają podstawy będące kwadratami, a ich objętości są równe, to długości boków tych kwadratów muszą być identyczne. W konsekwencji, ich pola powierzchni całkowitej również będą równe.
Graniastosłup o podstawie prostokątnej kontra graniastosłup o podstawie w kształcie równoległoboku o tej samej powierzchni: Możliwe jest dobranie wymiarów prostokąta i równoległoboku w taki sposób, aby ich pola były identyczne, ale obwody różne. W takim przypadku, graniastosłup o podstawie równoległobocznej będzie miał inne pole powierzchni bocznej i całkowitej niż graniastosłup o podstawie prostokątnej.

H2 Wpływ wysokości na parametry

Skoro wysokość jest stała i wynosi 5, wpływa ona liniowo na objętość i pole powierzchni bocznej. Zwiększenie pola podstawy powoduje proporcjonalny wzrost objętości. Zwiększenie obwodu podstawy powoduje proporcjonalny wzrost pola powierzchni bocznej. Pole powierzchni całkowitej jest bardziej złożone, ponieważ zależy zarówno od pola podstawy, jak i obwodu.

Podsumowując, analiza dwóch graniastosłupów prostych czworokątnych o tej samej wysokości wymaga uwzględnienia zarówno kształtu, jak i wymiarów ich podstaw. Równość wysokości upraszcza niektóre obliczenia, ale różnice w kształcie podstaw mają kluczowy wpływ na objętość i pole powierzchni.