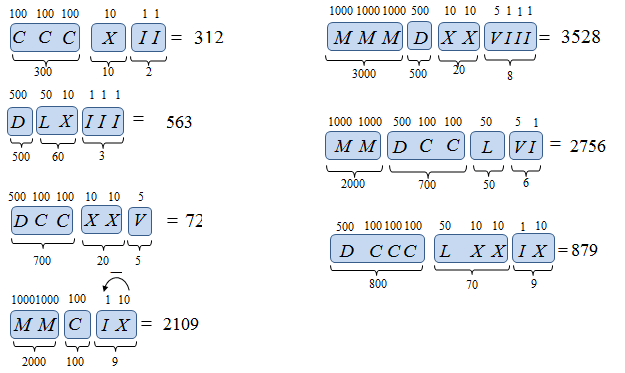Duże Liczby W Systemie Rzymskim

System rzymski, choć kojarzony głównie z cyframi I, V, X, L, C, D i M, kryje w sobie pewne wyzwania, gdy chcemy przedstawić duże liczby. Wbrew powszechnemu przekonaniu, Rzymianie radzili sobie z reprezentowaniem liczb większych niż 3999, choć robili to z użyciem specyficznych konwencji. Ten artykuł ma na celu przybliżenie metod zapisu dużych liczb w systemie rzymskim, przedstawiając zarówno teoretyczne podstawy, jak i praktyczne przykłady.
Podstawowe Zasady Zapisu Cyfr Rzymskich
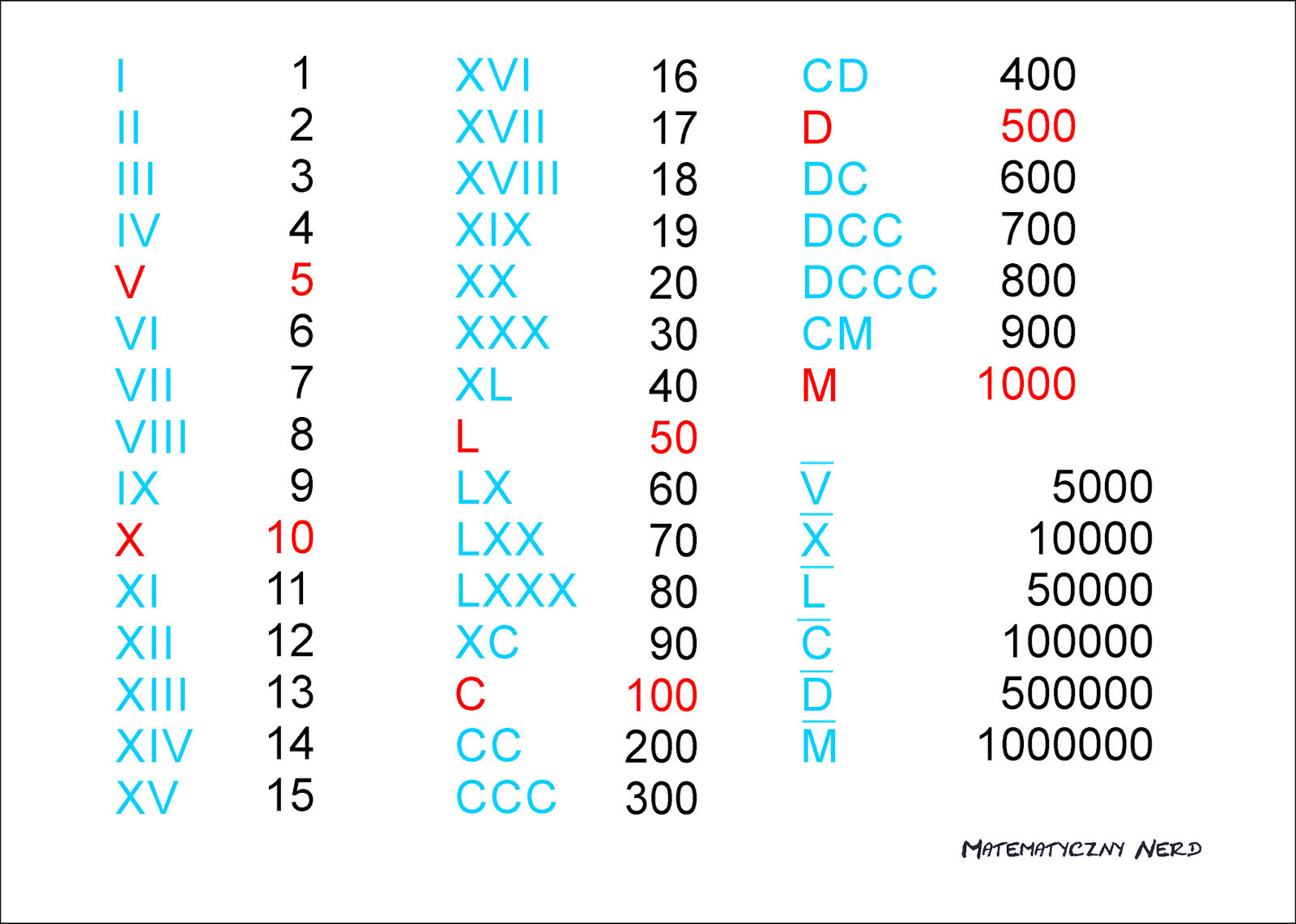
Zanim przejdziemy do dużych liczb, warto przypomnieć sobie podstawowe zasady zapisu rzymskiego. Kluczowe symbole to:
- I = 1
- V = 5
- X = 10
- L = 50
- C = 100
- D = 500
- M = 1000
Liczby tworzy się poprzez dodawanie i odejmowanie. Mniejsze cyfry umieszczone przed większymi oznaczają odejmowanie (np. IV = 4), a umieszczone po większych – dodawanie (np. VI = 6). Ważne jest, że odejmowanie stosuje się tylko dla bezpośrednio mniejszych cyfr (np. można zapisać IX = 9, ale nie IC = 99).
Ograniczenia Podstawowego Systemu
Tradycyjnie, system rzymski ma ograniczenia. Największą liczbą, którą da się zapisać bez specjalnych modyfikacji, jest MMMCMXCIX, czyli 3999. Co jednak z liczbami większymi?
Vinculum – Kreska Nad Cyfrą
Jednym ze sposobów na reprezentowanie większych liczb był vinculum, czyli kreska umieszczana nad cyfrą. Kreska nad cyfrą oznacza, że jej wartość należy pomnożyć przez 1000. Na przykład:
- V = 5000
- X = 10 000
- L = 50 000
- C = 100 000
- D = 500 000
- M = 1 000 000
Używając vinculum, można zapisywać znacznie większe liczby. Na przykład, liczba 45 678 byłaby zapisana jako XLVDCLXXVIII.
Podwójny Vinculum
Dla jeszcze większych liczb stosowano podwójny vinculum (czasem nazywany koroną lub ramką). Podwójna kreska nad cyfrą oznacza pomnożenie jej wartości przez 1 000 000. Zatem:
- I = 1 000 000
- V = 5 000 000
- X = 10 000 000
Na przykład, XVCMLXXXII reprezentuje 10 005 982.
Apostrophus i Inversus C
Inną metodą, stosowaną zwłaszcza w starożytności, było użycie apostrophus (odwrócone C) i jego lustrzanego odbicia. Oznaczały one mnożenie przez tysiąc.
Symbol (I) reprezentował 1000, a ((I)) reprezentowało 100 000. (((I))) to już 10 000 000. Te symbole rzadko były używane, ale istnieją dowody na ich występowanie w starożytnych tekstach.
Również |Ɔ (inversus C) oznaczało 500, a |ƆƆ oznaczało 5000, a |ƆƆƆ oznaczało 50 000. Ta notacja była mniej powszechna niż vinculum.
Praktyczne Przyklady i Zastosowania
Znalezienie konkretnych przykładów użycia dużych liczb rzymskich w starożytności nie jest łatwe, ponieważ większość dokumentów historycznych (np. inskrypcje) zazwyczaj nie wymagała reprezentowania bardzo dużych kwot. Jednakże, można znaleźć przykłady w traktatach matematycznych, rachunkach handlowych i zapisach administracyjnych.
Wyobraźmy sobie, że Rzymianin musiał zapisać liczbę 1 234 567. Używając vinculum i podstawowych cyfr rzymskich, mógłby to zapisać jako MCCXXXIVDLXVII.
Inny przykład: 5 789 432 można by zapisać jako VDCCLXXXIXCDXXXII.
Choć w dzisiejszych czasach nie używamy systemu rzymskiego na co dzień do operacji matematycznych, znajomość jego zasad, zwłaszcza tych dotyczących dużych liczb, pozwala lepiej zrozumieć historię matematyki i systemów liczbowych.
Realne Dane Historyczne (ograniczone)
Bezpośrednie przykłady historyczne użycia notacji vinculum dla bardzo dużych liczb są trudne do znalezienia w powszechnie dostępnych źródłach. Jednakże, archeolodzy i historycy znajdują fragmenty dokumentów (np. na tabliczkach woskowych), gdzie liczby przekraczają 3999 i używają form zapisu sugerujących zastosowanie vinculum lub innych metod zwiększania zakresu liczb.
W rachunkach dotyczących dużych transakcji handlowych lub spisu ludności, notacja rzymska (w rozwiniętej formie) musiała być stosowana, aby reprezentować tysiące i dziesiątki tysięcy. Niestety, kompletne i dobrze zachowane dokumenty z takimi liczbami są rzadkością.
Wyzwania i Niedogodności Systemu Rzymskiego
Mimo istnienia metod zapisu dużych liczb, system rzymski nie był idealny. Brak zera i addytywno-subtraktywny charakter utrudniały wykonywanie skomplikowanych obliczeń. Dodawanie, odejmowanie, mnożenie i dzielenie wymagały użycia abakusa lub innych narzędzi wspomagających. To właśnie dlatego system rzymski został ostatecznie zastąpiony przez bardziej efektywny system arabski, który używamy do dziś.
Kolejnym problemem była niejednolitość notacji. Różni skrybowie mogli stosować nieco odmienne konwencje, co prowadziło do niejasności i potencjalnych błędów. Brak standaryzacji utrudniał komunikację i wymianę informacji liczbowych.
Podsumowanie i Wnioski
System rzymski, choć z pozoru prosty, oferuje rozwiązania dla zapisu dużych liczb. Użycie vinculum, podwójnego vinculum oraz innych notacji (apostrophus, inversus C) pozwalało na przedstawianie liczb rzędu tysięcy, setek tysięcy, a nawet milionów. Pomimo swoich ograniczeń i niedogodności, system rzymski odegrał ważną rolę w historii matematyki i kultury. Zrozumienie zasad zapisu dużych liczb rzymskich pozwala docenić pomysłowość starożytnych Rzymian i lepiej zrozumieć ewolucję systemów liczbowych.
Dalsze badania nad starożytnymi dokumentami i inskrypcjami mogą ujawnić więcej przykładów użycia dużych liczb rzymskich w praktyce. Zachęcam do zgłębiania historii matematyki i eksplorowania różnych systemów liczbowych, aby poszerzyć swoją wiedzę i spojrzeć na liczby z nowej perspektywy. Może odkryjesz fascynujące, zapomniane metody obliczeń!