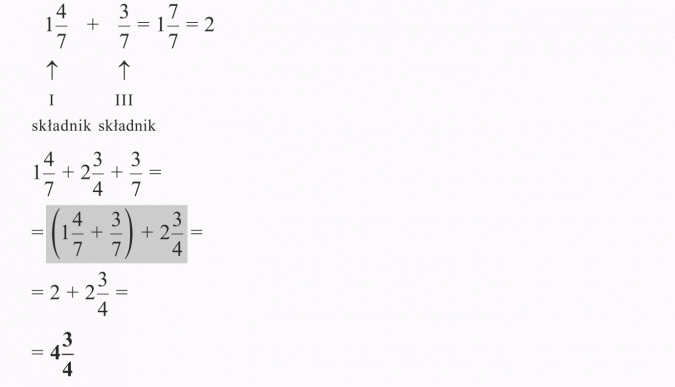Dodawanie Ułamków Klasa 4 Zadania

Witajcie, młodzi matematycy! Wkraczamy w świat ułamków! Na pewno słyszeliście o nich i być może już trochę o nich wiecie. Dziś skupimy się na dodawaniu ułamków, co jest kluczową umiejętnością w matematyce klasy 4. Dodawanie ułamków może wydawać się trudne na początku, ale z odpowiednim podejściem i odrobiną praktyki, stanie się ono dla Was łatwe i przyjemne. Ten artykuł ma na celu pomóc Wam zrozumieć, jak to robić krok po kroku.

Dlaczego Dodawanie Ułamków Jest Ważne?

Zanim przejdziemy do szczegółów, warto zrozumieć, dlaczego w ogóle uczymy się dodawać ułamki. Ułamki są wszędzie wokół nas! Od przepisów kulinarnych, gdzie potrzebujemy np. 1/2 szklanki mąki, po dzielenie pizzy na kawałki, które chcemy zjeść. Zrozumienie ułamków i umiejętność wykonywania na nich operacji matematycznych, takich jak dodawanie, jest niezbędne w wielu sytuacjach codziennego życia.

Pomaga także w rozwijaniu logicznego myślenia i umiejętności rozwiązywania problemów. Kiedy opanujesz dodawanie ułamków, poczujesz większą pewność siebie w matematyce i łatwiej będzie Ci się uczyć trudniejszych zagadnień w przyszłości.

Podstawy Ułamków: Przypomnienie

Zanim zaczniemy dodawać ułamki, upewnijmy się, że dobrze rozumiemy, co to jest ułamek. Ułamek składa się z dwóch części:

Licznika: To liczba nad kreską ułamkową. Mówi nam, ile części całości mamy.
Mianownika: To liczba pod kreską ułamkową. Mówi nam, na ile równych części została podzielona całość.

Na przykład, w ułamku 3/4, 3 to licznik, a 4 to mianownik. Oznacza to, że mamy 3 części z całości podzielonej na 4 równe części.

Ułamki Właściwe i Niewłaściwe

Ważne jest również rozróżnienie między ułamkami właściwymi i niewłaściwymi:

Ułamek właściwy: Licznik jest mniejszy od mianownika (np. 1/2, 2/3, 3/4).
Ułamek niewłaściwy: Licznik jest większy lub równy mianownikowi (np. 4/3, 5/2, 7/7). Ułamek niewłaściwy można zamienić na liczbę mieszaną.

Liczba mieszana składa się z liczby całkowitej i ułamka właściwego (np. 1 1/3). 4/3 to to samo, co 1 1/3.

Dodawanie Ułamków o Tych Samych Mianownikach

Zacznijmy od najprostszego przypadku: dodawania ułamków, które mają ten sam mianownik. To naprawdę proste!

Zasada: Aby dodać ułamki o tych samych mianownikach, dodajemy liczniki, a mianownik pozostawiamy bez zmian.

Przykład:

1/4 + 2/4 = (1 + 2) / 4 = 3/4

Wyobraźmy sobie, że mamy tort podzielony na 4 kawałki. Zjadamy jeden kawałek (1/4 tortu), a potem jeszcze dwa kawałki (2/4 tortu). Razem zjedliśmy 3 kawałki (3/4 tortu).

Inny przykład:

3/8 + 1/8 + 2/8 = (3 + 1 + 2) / 8 = 6/8

Pamiętaj, żeby zawsze sprawdzać, czy wynik można uprościć. W tym przypadku, 6/8 można uprościć do 3/4, dzieląc licznik i mianownik przez 2.

Dodawanie Ułamków o Różnych Mianownikach

Dodawanie ułamków o różnych mianownikach jest trochę trudniejsze, ale nadal do opanowania! Kluczem jest sprowadzenie ułamków do wspólnego mianownika.

Co to jest Wspólny Mianownik?

Wspólny mianownik to liczba, która jest wielokrotnością wszystkich mianowników w dodawanych ułamkach. Najczęściej używamy najmniejszego wspólnego mianownika (NWW), ponieważ ułatwia to obliczenia.

Przykład: Chcemy dodać 1/2 + 1/3.

Mianowniki to 2 i 3. Musimy znaleźć NWW liczb 2 i 3. Wielokrotności 2 to: 2, 4, 6, 8... Wielokrotności 3 to: 3, 6, 9, 12... Najmniejszą wspólną wielokrotnością 2 i 3 jest 6. Zatem, wspólnym mianownikiem będzie 6.

Jak Sprowadzić Ułamki do Wspólnego Mianownika?

Aby sprowadzić ułamek do nowego mianownika, musimy pomnożyć zarówno licznik, jak i mianownik przez tę samą liczbę. Ta liczba to wynik podzielenia nowego mianownika przez stary mianownik.

W naszym przykładzie (1/2 + 1/3):

Dla 1/2: Dzielimy nowy mianownik (6) przez stary mianownik (2): 6 / 2 = 3. Mnożymy licznik i mianownik 1/2 przez 3: (1 * 3) / (2 * 3) = 3/6
Dla 1/3: Dzielimy nowy mianownik (6) przez stary mianownik (3): 6 / 3 = 2. Mnożymy licznik i mianownik 1/3 przez 2: (1 * 2) / (3 * 2) = 2/6

Teraz mamy: 3/6 + 2/6. Możemy dodać ułamki, ponieważ mają ten sam mianownik:

3/6 + 2/6 = (3 + 2) / 6 = 5/6

Inny przykład: 1/4 + 2/5

Znajdujemy NWW dla 4 i 5. Wielokrotności 4 to: 4, 8, 12, 16, 20... Wielokrotności 5 to: 5, 10, 15, 20... NWW wynosi 20.

Dla 1/4: 20 / 4 = 5. Mnożymy licznik i mianownik przez 5: (1 * 5) / (4 * 5) = 5/20
Dla 2/5: 20 / 5 = 4. Mnożymy licznik i mianownik przez 4: (2 * 4) / (5 * 4) = 8/20

Dodajemy: 5/20 + 8/20 = 13/20

Dodawanie Liczb Mieszanych

Dodawanie liczb mieszanych można zrobić na dwa sposoby:

Sposób 1: Dodajemy liczby całkowite oddzielnie, a następnie ułamki. Jeśli suma ułamków jest ułamkiem niewłaściwym, zamieniamy go na liczbę mieszaną i dodajemy do sumy liczb całkowitych.
Sposób 2: Zamieniamy liczby mieszane na ułamki niewłaściwe, a następnie dodajemy ułamki jak zwykle. Na koniec, zamieniamy wynik z powrotem na liczbę mieszaną (jeśli to konieczne).

Przykład (Sposób 1): 2 1/4 + 1 1/2

Dodajemy liczby całkowite: 2 + 1 = 3

Dodajemy ułamki: 1/4 + 1/2. Musimy znaleźć wspólny mianownik. NWW dla 4 i 2 to 4.

Sprowadzamy 1/2 do mianownika 4: (1 * 2) / (2 * 2) = 2/4

Dodajemy ułamki: 1/4 + 2/4 = 3/4

Łączymy wyniki: 3 + 3/4 = 3 3/4

Przykład (Sposób 2): 2 1/4 + 1 1/2

Zamieniamy 2 1/4 na ułamek niewłaściwy: (2 * 4 + 1) / 4 = 9/4

Zamieniamy 1 1/2 na ułamek niewłaściwy: (1 * 2 + 1) / 2 = 3/2

Znajdujemy wspólny mianownik (NWW dla 4 i 2 to 4).

Sprowadzamy 3/2 do mianownika 4: (3 * 2) / (2 * 2) = 6/4

Dodajemy ułamki: 9/4 + 6/4 = 15/4

Zamieniamy 15/4 na liczbę mieszaną: 15 / 4 = 3 reszty 3, więc 15/4 = 3 3/4

Przykłady z Życia Codziennego

Spójrzmy na kilka przykładów z życia codziennego, gdzie dodawanie ułamków może się przydać:

Gotowanie: Przepis na ciasto wymaga 1/2 szklanki mąki pszennej i 1/4 szklanki mąki ziemniaczanej. Ile mąki potrzebujesz łącznie? (1/2 + 1/4 = 3/4 szklanki)
Sport: Podczas biegu, Kasia przebiegła 1/3 trasy, a Janek 2/5 trasy. Jaką część trasy przebiegli razem? (1/3 + 2/5 = 11/15 trasy)
Dzielenie pizzy: Pizza została podzielona na 8 kawałków. Zjadłeś 2 kawałki (2/8 pizzy), a Twój brat zjadł 3 kawałki (3/8 pizzy). Ile pizzy zostało zjedzone łącznie? (2/8 + 3/8 = 5/8 pizzy)

Zadania do Ćwiczeń

Aby dobrze opanować dodawanie ułamków, potrzebna jest praktyka. Oto kilka zadań do samodzielnego rozwiązania:

1/5 + 2/5 = ?
3/7 + 2/7 + 1/7 = ?
1/3 + 1/6 = ?
2/5 + 1/4 = ?
1 1/2 + 2 1/4 = ?
3 2/3 + 1 1/6 = ?

Sprawdź swoje odpowiedzi i w razie potrzeby, wróć do wcześniejszych części artykułu, aby powtórzyć materiał.

Podsumowanie

Dodawanie ułamków to ważna umiejętność, która przydaje się w wielu sytuacjach życiowych. Pamiętaj o podstawowych zasadach: jeśli ułamki mają ten sam mianownik, dodajemy liczniki. Jeśli mają różne mianowniki, musimy sprowadzić je do wspólnego mianownika. Regularna praktyka jest kluczem do sukcesu!

Nie zrażaj się trudnościami! Z każdym rozwiązanym zadaniem będziesz coraz lepszy. Powodzenia!