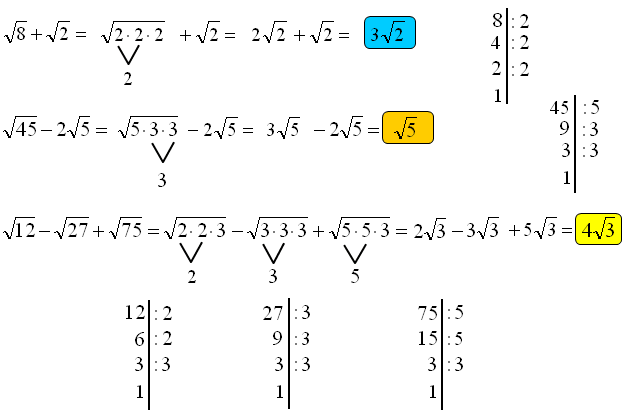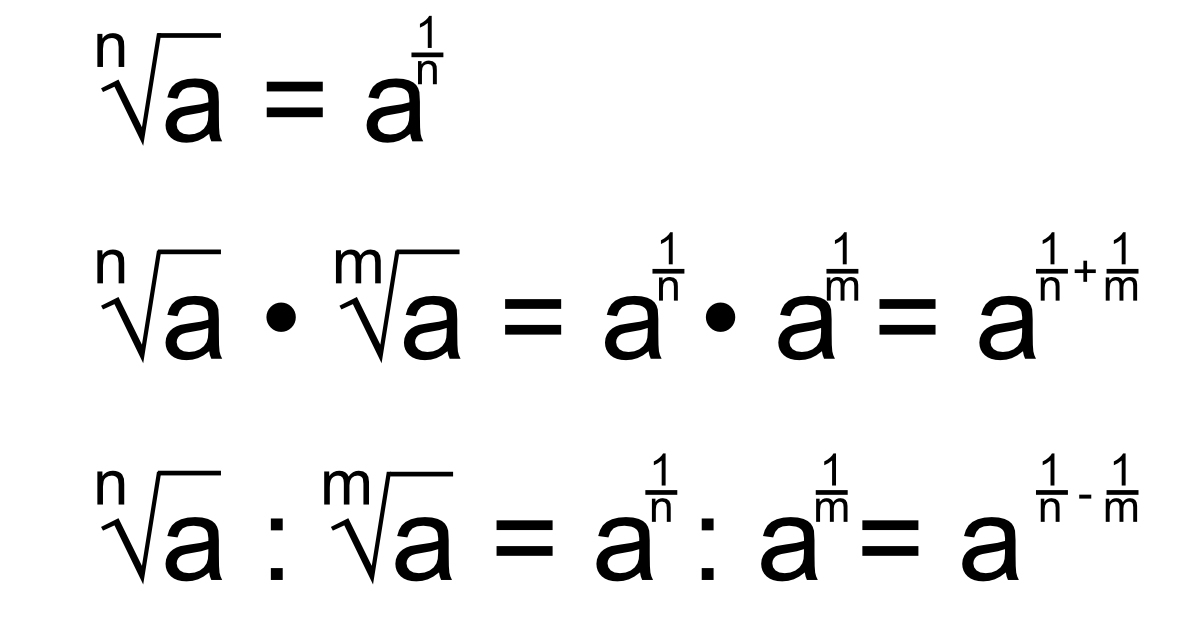Dodawanie Pierwiastków O Różnych Podstawach

Czy kiedykolwiek zastanawiałeś się, jak dodać do siebie pierwiastki, które na pierwszy rzut oka wydają się kompletnie różne? To pytanie może wydawać się skomplikowane, zwłaszcza dla osób stawiających pierwsze kroki w świecie matematyki. Ale spokojnie! Ten artykuł został stworzony właśnie dla Ciebie – ucznia, studenta, czy każdego, kto chce zrozumieć, jak poradzić sobie z dodawaniem pierwiastków o różnych podstawach.

Naszym celem jest przedstawienie jasnych i zrozumiałych zasad dodawania pierwiastków, nawet tych z pozoru niekompatybilnych. Zamiast zanurzać się w skomplikowanych wzorach, skupimy się na praktycznych przykładach i logicznym rozumowaniu. Gotowy? Zaczynamy!

Czym są Pierwiastki i Dlaczego Sprawiają Problemy?

Zanim przejdziemy do sedna, upewnijmy się, że wszyscy rozumiemy, czym właściwie jest pierwiastek. W uproszczeniu, pierwiastek kwadratowy z liczby x to taka liczba y, która pomnożona przez samą siebie daje x. Na przykład, pierwiastek kwadratowy z 9 to 3, ponieważ 3 * 3 = 9. Analogicznie, pierwiastek sześcienny z 8 to 2, ponieważ 2 * 2 * 2 = 8.

Problemy zaczynają się, gdy próbujemy dodać pierwiastki, które mają różne liczby pod pierwiastkiem, czyli tzw. podstawy. Nie możemy po prostu dodać ich do siebie tak, jak dodajemy jabłka i jabłka. Musimy najpierw zrozumieć, kiedy i jak możemy je uprościć.

Kiedy Możemy Dodawać Pierwiastki?

Kluczowym pojęciem jest "podobne pierwiastki". Dwa pierwiastki są podobne, gdy mają ten sam stopień pierwiastka (np. pierwiastek kwadratowy, sześcienny, etc.) i tą samą liczbę pod pierwiastkiem. Dopiero wtedy możemy je dodać.

Spójrzmy na przykład:

√2 + 3√2 = 4√2 (To są podobne pierwiastki - oba są pierwiastkami kwadratowymi z 2)
√2 + √3 = ? (To nie są podobne pierwiastki - mają różne liczby pod pierwiastkiem)

Widzimy więc, że dodawanie jest możliwe tylko wtedy, gdy "wnętrze" pierwiastka jest identyczne. Ale co zrobić, gdy tak nie jest?

Upraszczanie Pierwiastków – Klucz do Sukcesu

Często, zanim będziemy mogli dodać pierwiastki, musimy je najpierw uprościć. Upraszczanie polega na wyciągnięciu czynników przed znak pierwiastka. Jak to zrobić? Rozłóżmy liczbę pod pierwiastkiem na czynniki pierwsze i poszukajmy kwadratów (lub sześcianów, jeśli mamy pierwiastek trzeciego stopnia) liczb.

Przykład 1: Uprośćmy √12

Rozkładamy 12 na czynniki pierwsze: 12 = 2 * 2 * 3 = 2² * 3
√12 = √(2² * 3)
Wyciągamy 2² przed pierwiastek jako 2: √12 = 2√3

Teraz, jeśli mieliśmy wyrażenie √12 + √3, możemy je uprościć:

√12 + √3 = 2√3 + √3 = 3√3

Przykład 2: Uprośćmy √50 + √18

Upraszczamy √50: 50 = 2 * 5 * 5 = 2 * 5² => √50 = √(2 * 5²) = 5√2
Upraszczamy √18: 18 = 2 * 3 * 3 = 2 * 3² => √18 = √(2 * 3²) = 3√2
Dodajemy: 5√2 + 3√2 = 8√2

Zauważ, jak uproszczenie pierwiastków pozwoliło nam zamienić problem w proste dodawanie!

Dodawanie Pierwiastków Sześciennych (i wyższych stopni)

Zasady dodawania pierwiastków sześciennych (i wyższych stopni) są analogiczne do tych dla pierwiastków kwadratowych. Różnica polega na tym, że szukamy czynników, które podniesione do potęgi równej stopniowi pierwiastka, dają liczbę pod pierwiastkiem.

Przykład: Uprośćmy ∛24 + ∛81

Upraszczamy ∛24: 24 = 2 * 2 * 2 * 3 = 2³ * 3 => ∛24 = ∛(2³ * 3) = 2∛3
Upraszczamy ∛81: 81 = 3 * 3 * 3 * 3 = 3³ * 3 => ∛81 = ∛(3³ * 3) = 3∛3
Dodajemy: 2∛3 + 3∛3 = 5∛3

Kiedy Uproszczenie Nie Pomoże?

Niestety, nie zawsze da się uprościć pierwiastki tak, aby stały się podobne. Na przykład, √7 + √11 nie da się uprościć, ponieważ 7 i 11 są liczbami pierwszymi. W takich przypadkach, po prostu zostawiamy wyrażenie w takiej postaci.

Praktyczne Porady i Wskazówki

Zawsze szukaj możliwości uproszczenia: To pierwszy krok. Rozkładaj liczby pod pierwiastkiem na czynniki pierwsze.
Zwracaj uwagę na stopień pierwiastka: Pamiętaj, że pierwiastek kwadratowy i sześcienny to różne operacje.
Ćwicz, ćwicz, ćwicz: Im więcej przykładów rozwiążesz, tym lepiej zrozumiesz zasady.
Nie bój się pytać: Jeśli masz wątpliwości, zapytaj nauczyciela, kolegę lub poszukaj odpowiedzi online.

Przykłady z Życia Wzięte

Choć pierwiastki mogą wydawać się abstrakcyjnym konceptem, mają wiele zastosowań w życiu codziennym, np.:

Obliczanie długości przekątnej kwadratu lub prostokąta: Używamy twierdzenia Pitagorasa, które zawiera pierwiastki.
Obliczanie pola powierzchni niektórych figur geometrycznych: Np. wzór na pole trójkąta równobocznego zawiera pierwiastek kwadratowy.
Fizyka: Obliczanie prędkości, energii potencjalnej i kinetycznej często wymaga użycia pierwiastków.
Inżynieria: Projektowanie mostów, budynków i innych konstrukcji wymaga precyzyjnych obliczeń, w których pierwiastki odgrywają ważną rolę.

Typowe Błędy, Których Należy Unikać

Podczas dodawania pierwiastków łatwo popełnić błędy. Oto kilka z nich:

Dodawanie pierwiastków o różnych podstawach bez upraszczania: Pamiętaj, że √2 + √3 ≠ √5
Pomijanie stopnia pierwiastka: Upewnij się, że dodajesz tylko pierwiastki tego samego stopnia.
Błędne upraszczanie: Sprawdź, czy poprawnie rozłożyłeś liczbę na czynniki pierwsze i wyciągnąłeś czynniki przed pierwiastek.

Ćwiczenie 1: Uprość i dodaj √27 + √12 + √75

√27 = √(3² * 3) = 3√3

√12 = √(2² * 3) = 2√3

√75 = √(5² * 3) = 5√3

3√3 + 2√3 + 5√3 = 10√3

Ćwiczenie 2: Uprość i dodaj ∛16 + ∛54

∛16 = ∛(2³ * 2) = 2∛2

∛54 = ∛(3³ * 2) = 3∛2

2∛2 + 3∛2 = 5∛2

Podsumowanie i Co Dalej?

Dodawanie pierwiastków o różnych podstawach może wydawać się trudne na początku, ale dzięki upraszczaniu i zrozumieniu zasad, staje się prostsze. Pamiętaj, żeby szukać podobnych pierwiastków, a jeśli ich nie ma, spróbuj uprościć te, które masz.

Teraz, kiedy znasz już podstawy, zachęcamy do dalszej eksploracji świata pierwiastków! Spróbuj rozwiązywać bardziej skomplikowane zadania, poszukaj informacji o innych operacjach na pierwiastkach (np. mnożenie, dzielenie), a być może odkryjesz w sobie talent do matematyki. Pamiętaj, że matematyka to nie tylko wzory, ale przede wszystkim logiczne myślenie i rozwiązywanie problemów.

Życzymy powodzenia w dalszej nauce!