Dodawanie Liczb O Tych Samych Potęgach

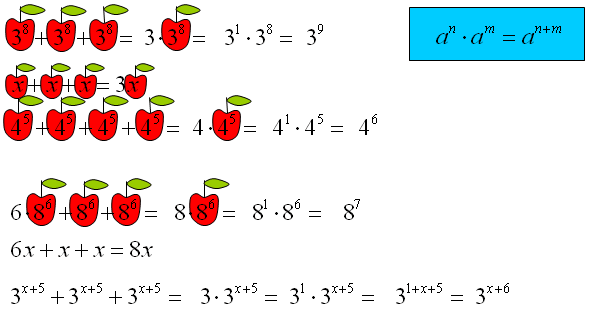
Często w matematyce, zwłaszcza w algebrze, spotykamy się z koniecznością dodawania wyrażeń algebraicznych, które zawierają potęgi. Dodawanie liczb o tych samych potęgach jest operacją, która wymaga pewnej ostrożności i zrozumienia zasad dotyczących wyrażeń podobnych. W tym artykule szczegółowo omówimy, jak dodawać liczby o tych samych potęgach, przedstawimy liczne przykłady i zastosowania.

Co to są wyrażenia podobne?

Zanim przejdziemy do samego dodawania, ważne jest, aby zrozumieć, co rozumiemy przez wyrażenia podobne. Wyrażenia algebraiczne są podobne, jeśli mają te same zmienne podniesione do tych samych potęg. Na przykład, 3x² i 5x² są wyrażeniami podobnymi, ponieważ oba zawierają zmienną 'x' podniesioną do potęgi 2. Natomiast 3x² i 5x³ nie są podobne, ponieważ potęgi są różne.

Kluczowe jest, aby zrozumieć, że dodawać możemy jedynie wyrażenia podobne. To ograniczenie wynika z podstawowych praw algebry.

Jak dodawać liczby o tych samych potęgach - krok po kroku

Proces dodawania liczb o tych samych potęgach jest dość prosty, pod warunkiem, że wyrażenia są podobne. Oto kroki, które należy wykonać:

Krok 1: Sprawdź, czy wyrażenia są podobne

Upewnij się, że wszystkie wyrażenia, które chcesz dodać, mają te same zmienne i te same potęgi. Jeżeli tak nie jest, nie możesz ich bezpośrednio dodać.

Krok 2: Dodaj współczynniki

Współczynnik to liczba, która stoi przed zmienną. Na przykład, w wyrażeniu 5x² współczynnik wynosi 5. Dodaj współczynniki wszystkich podobnych wyrażeń.

Krok 3: Przepisz zmienną z potęgą

Po dodaniu współczynników, przepisz zmienną z potęgą. To właśnie ona definiuje, że wyrażenia są podobne.

Przykłady dodawania liczb o tych samych potęgach

Aby lepiej zrozumieć ten proces, przyjrzyjmy się kilku przykładom:

• Przykład 1: 3x² + 5x² = (3+5)x² = 8x²
• Przykład 2: -2y³ + 7y³ = (-2+7)y³ = 5y³
• Przykład 3: 4ab² + 2ab² - ab² = (4+2-1)ab² = 5ab²
• Przykład 4: 6z⁴ - 8z⁴ + 3z⁴ = (6-8+3)z⁴ = z⁴

Zauważ, że w każdym z tych przykładów dodawaliśmy lub odejmowaliśmy tylko współczynniki, a zmienna z potęgą pozostała bez zmian.

Wyrażenia, które nie są podobne

Co się dzieje, gdy próbujemy dodać wyrażenia, które nie są podobne? W takim przypadku nie możemy ich połączyć w jedno wyrażenie. Po prostu zostawiamy je oddzielnie.

Na przykład, jeśli mamy wyrażenie 3x² + 5x³, nie możemy go uprościć. To wyrażenie pozostaje w takiej formie, dopóki nie będziemy mieli więcej informacji lub możliwości zastosowania innych operacji matematycznych.

Zastosowania dodawania liczb o tych samych potęgach

Dodawanie liczb o tych samych potęgach ma wiele zastosowań w różnych dziedzinach, w tym:

• Algebra: Upraszczanie wyrażeń algebraicznych, rozwiązywanie równań.
• Fizyka: Obliczanie sum sił, energii, i innych wielkości fizycznych.
• Inżynieria: Projektowanie obwodów elektrycznych, obliczanie obciążeń konstrukcyjnych.
• Informatyka: Analiza algorytmów, optymalizacja kodu.

Na przykład, rozważmy problem obliczenia całkowitego kosztu produkcji, gdzie koszt materiałów jest opisany wyrażeniem 2x², a koszt robocizny wyrażeniem 3x². Całkowity koszt to suma tych dwóch wyrażeń: 2x² + 3x² = 5x². Gdzie 'x' może reprezentować jednostkę produktu.

Podsumowanie

Dodawanie liczb o tych samych potęgach jest podstawową umiejętnością w algebrze. Kluczem do sukcesu jest rozpoznawanie wyrażeń podobnych i dodawanie tylko ich współczynników. Pamiętaj, że dodawanie wyrażeń, które nie są podobne, nie jest możliwe bez dodatkowych operacji lub informacji. Zrozumienie tych zasad pozwala na upraszczanie wyrażeń algebraicznych, rozwiązywanie równań i stosowanie tej wiedzy w różnych dziedzinach nauki i techniki.

Ćwiczenie różnych przykładów pomoże Ci utrwalić tę umiejętność i zwiększyć pewność siebie w rozwiązywaniu bardziej złożonych problemów matematycznych. Pamiętaj, praktyka czyni mistrza!