Dodawanie I Odejmowanie Ułamków Zwykłych O Różnych Mianownikach

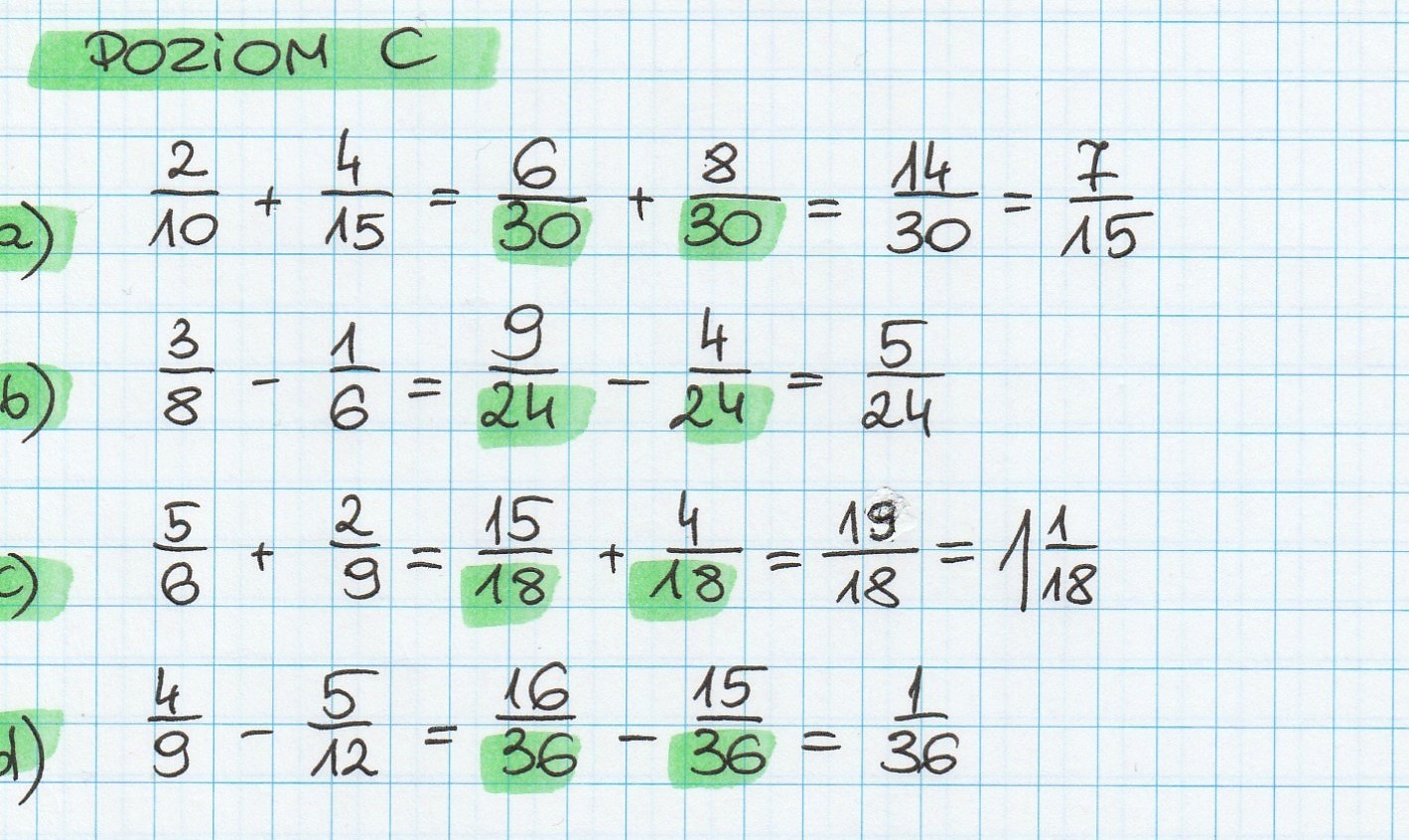
Dodawanie i odejmowanie ułamków zwykłych o różnych mianownikach bywa wyzwaniem, ale dzięki kilku prostym krokom, można je opanować bez większego problemu. Pamiętaj, kluczem jest sprowadzenie ułamków do wspólnego mianownika.

Zacznijmy od najprostszego przykładu: 1/2 + 1/4. Zauważamy, że mianowniki są różne – 2 i 4. Szukamy najmniejszej wspólnej wielokrotności (NWW) liczb 2 i 4. W tym przypadku NWW wynosi 4. Teraz pierwszy ułamek, 1/2, musimy przekształcić tak, aby w mianowniku mieć 4. Aby to zrobić, mnożymy licznik i mianownik ułamka 1/2 przez 2: (1 * 2) / (2 * 2) = 2/4. Teraz mamy: 2/4 + 1/4. Mianowniki są takie same, więc dodajemy liczniki: 2 + 1 = 3. Wynik to 3/4.

Przejdźmy do odejmowania: 2/3 - 1/6. Mamy mianowniki 3 i 6. NWW liczb 3 i 6 to 6. Ułamek 2/3 przekształcamy mnożąc licznik i mianownik przez 2: (2 * 2) / (3 * 2) = 4/6. Teraz mamy: 4/6 - 1/6. Odejmujemy liczniki: 4 - 1 = 3. Wynik to 3/6. Możemy jeszcze uprościć ten ułamek, dzieląc licznik i mianownik przez 3: (3 / 3) / (6 / 3) = 1/2.

Spróbujmy czegoś trudniejszego: 3/5 + 2/7. Mamy mianowniki 5 i 7. NWW liczb 5 i 7 to 35. Ułamek 3/5 przekształcamy mnożąc licznik i mianownik przez 7: (3 * 7) / (5 * 7) = 21/35. Ułamek 2/7 przekształcamy mnożąc licznik i mianownik przez 5: (2 * 5) / (7 * 5) = 10/35. Teraz mamy: 21/35 + 10/35. Dodajemy liczniki: 21 + 10 = 31. Wynik to 31/35.

A co z liczbami mieszanymi? Spróbujmy: 1 1/2 + 2 1/3. Najpierw zamieniamy liczby mieszane na ułamki niewłaściwe. 1 1/2 = (1 * 2 + 1) / 2 = 3/2. 2 1/3 = (2 * 3 + 1) / 3 = 7/3. Teraz mamy: 3/2 + 7/3. Mianowniki to 2 i 3. NWW liczb 2 i 3 to 6. Ułamek 3/2 przekształcamy mnożąc licznik i mianownik przez 3: (3 * 3) / (2 * 3) = 9/6. Ułamek 7/3 przekształcamy mnożąc licznik i mianownik przez 2: (7 * 2) / (3 * 2) = 14/6. Teraz mamy: 9/6 + 14/6. Dodajemy liczniki: 9 + 14 = 23. Wynik to 23/6. Możemy zamienić to z powrotem na liczbę mieszaną: 23 / 6 = 3 reszty 5, więc wynik to 3 5/6.

Pamiętaj, że upraszczanie ułamków to ważny krok. Jeśli wynik można uprościć, zawsze to rób. Na przykład, 6/8 można uprościć dzieląc licznik i mianownik przez 2: (6 / 2) / (8 / 2) = 3/4.

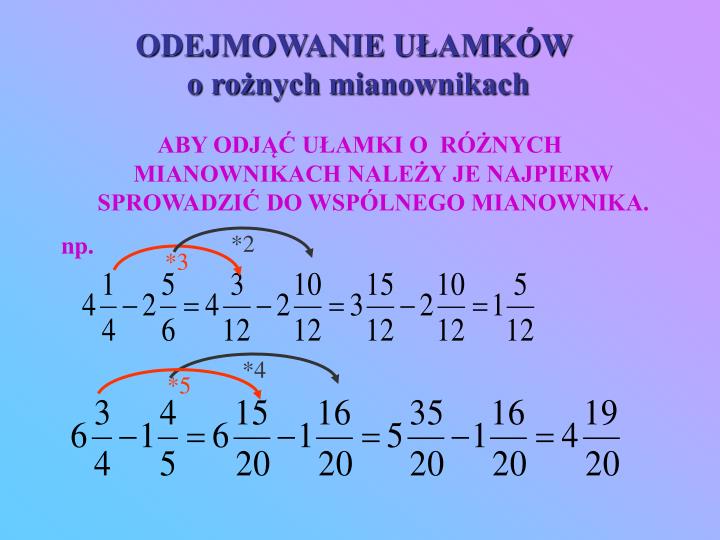
Oto kilka przykładów z odejmowaniem liczb mieszanych: 3 1/4 - 1 1/2. Najpierw zamieniamy na ułamki niewłaściwe: 3 1/4 = (3 * 4 + 1) / 4 = 13/4. 1 1/2 = (1 * 2 + 1) / 2 = 3/2. Teraz mamy: 13/4 - 3/2. Mianowniki to 4 i 2. NWW liczb 4 i 2 to 4. Ułamek 3/2 przekształcamy mnożąc licznik i mianownik przez 2: (3 * 2) / (2 * 2) = 6/4. Teraz mamy: 13/4 - 6/4. Odejmujemy liczniki: 13 - 6 = 7. Wynik to 7/4. Zamieniamy na liczbę mieszaną: 7 / 4 = 1 reszty 3, więc wynik to 1 3/4.

Co zrobić, gdy odejmujemy ułamek od liczby całkowitej? Na przykład: 5 - 2/3. Myślimy o liczbie 5 jako o ułamku 5/1. Teraz mamy: 5/1 - 2/3. Mianowniki to 1 i 3. NWW liczb 1 i 3 to 3. Ułamek 5/1 przekształcamy mnożąc licznik i mianownik przez 3: (5 * 3) / (1 * 3) = 15/3. Teraz mamy: 15/3 - 2/3. Odejmujemy liczniki: 15 - 2 = 13. Wynik to 13/3. Zamieniamy na liczbę mieszaną: 13 / 3 = 4 reszty 1, więc wynik to 4 1/3.

Rozwiązywanie bardziej skomplikowanych przykładów

Spójrzmy na bardziej rozbudowany przykład: 2 1/2 + 1 3/4 - 3/8. Najpierw zamieniamy liczby mieszane na ułamki niewłaściwe: 2 1/2 = (2 * 2 + 1) / 2 = 5/2. 1 3/4 = (1 * 4 + 3) / 4 = 7/4. Teraz mamy: 5/2 + 7/4 - 3/8. Mianowniki to 2, 4 i 8. NWW liczb 2, 4 i 8 to 8. Ułamek 5/2 przekształcamy mnożąc licznik i mianownik przez 4: (5 * 4) / (2 * 4) = 20/8. Ułamek 7/4 przekształcamy mnożąc licznik i mianownik przez 2: (7 * 2) / (4 * 2) = 14/8. Teraz mamy: 20/8 + 14/8 - 3/8. Dodajemy i odejmujemy liczniki: 20 + 14 - 3 = 31. Wynik to 31/8. Zamieniamy na liczbę mieszaną: 31 / 8 = 3 reszty 7, więc wynik to 3 7/8.

Jak znaleźć Najmniejszą Wspólną Wielokrotność (NWW)?

Istnieje kilka sposobów na znalezienie NWW. Można wypisać wielokrotności każdej liczby i znaleźć najmniejszą, która występuje w obu listach. Na przykład, dla liczb 4 i 6:

Wielokrotności 4: 4, 8, 12, 16, 20, 24... Wielokrotności 6: 6, 12, 18, 24, 30...

Najmniejszą wspólną wielokrotnością jest 12.

Inna metoda to rozkład na czynniki pierwsze. Dla liczb 12 i 18:

12 = 2 * 2 * 3 18 = 2 * 3 * 3

NWW to iloczyn wszystkich czynników pierwszych, wziętych z największą krotnością, z jaką występują w rozkładach: 2 * 2 * 3 * 3 = 36.

Ćwiczenia

Aby utrwalić wiedzę, rozwiąż kilka przykładów:

1/3 + 1/5
3/4 - 1/8
1 1/2 + 2/5
2 3/4 - 1 1/3
5/6 + 1/9 - 1/3

Pamiętaj o sprowadzaniu do wspólnego mianownika i upraszczaniu wyników.

Kluczem do sukcesu jest praktyka. Im więcej przykładów rozwiążesz, tym łatwiej i szybciej będziesz dodawać i odejmować ułamki o różnych mianownikach. Nie zrażaj się początkowymi trudnościami, a z czasem operacje na ułamkach staną się dla Ciebie proste i intuicyjne. Powodzenia!