Dodawanie I Odejmowanie Ułamków Zwykłych Klasa 4 Pdf

Drodzy uczniowie klasy czwartej! Często pytacie mnie o ułamki zwykłe, a szczególnie o to, jak je dodawać i odejmować. Spróbuję to wytłumaczyć tak prosto, jak to możliwe, żebyście mogli bez problemu rozwiązywać zadania.

Na początek, przypomnijmy sobie, co to właściwie jest ułamek zwykły. Ułamek zwykły to liczba, która przedstawia część całości. Składa się z licznika i mianownika, oddzielonych kreską ułamkową. Na przykład, w ułamku 1/2 (czytamy "jedna druga"), 1 to licznik, a 2 to mianownik. Mianownik mówi nam, na ile równych części podzieliliśmy całość, a licznik mówi, ile z tych części bierzemy.

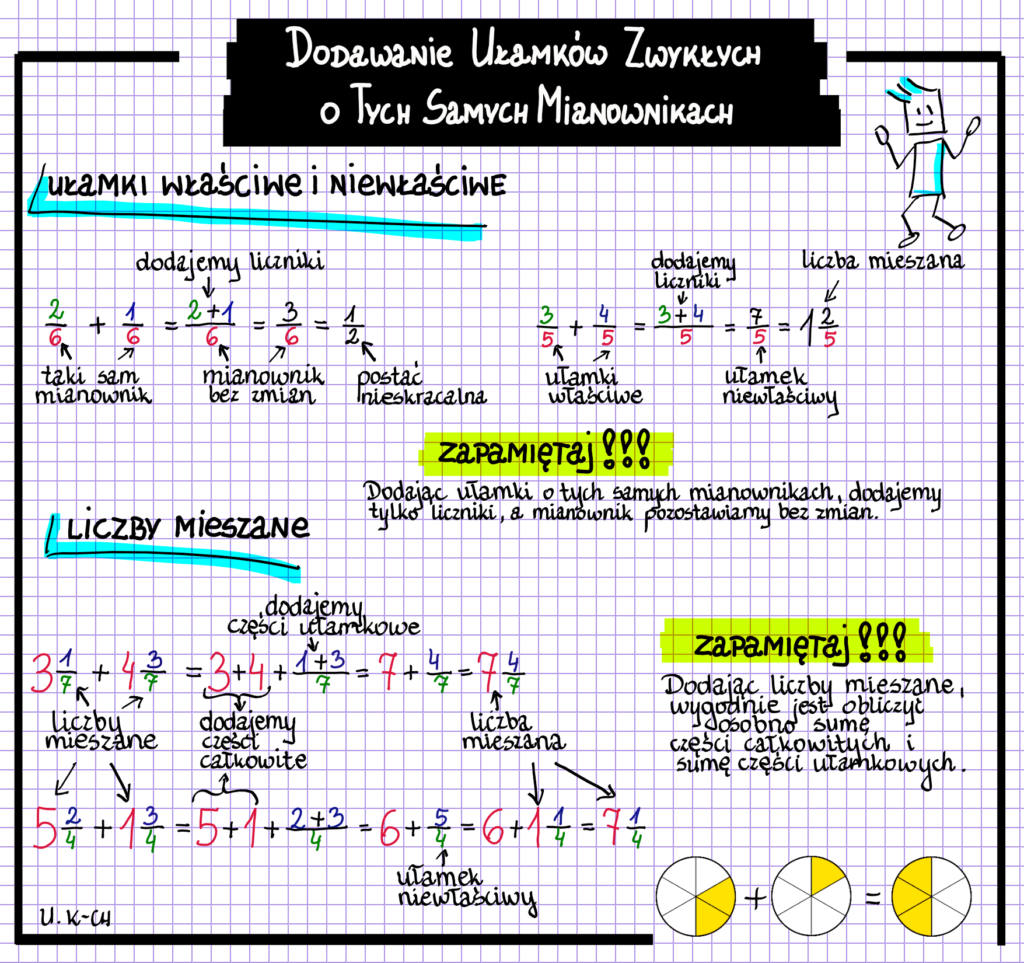
Dodawanie ułamków o tych samych mianownikach

Dodawanie ułamków jest proste, jeśli mają one te same mianowniki. Wyobraźcie sobie, że macie pizzę pokrojoną na 8 kawałków. Jeśli zjecie 2 kawałki (czyli 2/8 pizzy), a potem jeszcze 3 kawałki (3/8 pizzy), to łącznie zjecie 5 kawałków (5/8 pizzy).

Zatem, żeby dodać ułamki o tych samych mianownikach, dodajemy tylko liczniki, a mianownik zostawiamy bez zmian.

Przykład:

• 1/5 + 2/5 = (1+2)/5 = 3/5
• 3/8 + 4/8 = (3+4)/8 = 7/8
• 5/12 + 1/12 + 2/12 = (5+1+2)/12 = 8/12

Pamiętajcie, żeby po dodaniu ułamka sprawdzić, czy można go skrócić. Skracanie ułamków polega na podzieleniu licznika i mianownika przez ten sam dzielnik. W przykładzie 8/12, zarówno 8, jak i 12 można podzielić przez 4. Zatem:

8/12 = (8:4) / (12:4) = 2/3

Odejmowanie ułamków o tych samych mianownikach

Odejmowanie ułamków o tych samych mianownikach jest bardzo podobne do dodawania. Zamiast dodawać liczniki, odejmujemy je. Mianownik ponownie zostaje bez zmian.

Wyobraźcie sobie, że macie tort pokrojony na 6 kawałków. Jeśli macie 5 kawałków (5/6 tortu) i zjecie 2 kawałki (2/6 tortu), to zostanie Wam 3 kawałki (3/6 tortu).

Przykład:

• 4/7 - 1/7 = (4-1)/7 = 3/7
• 9/10 - 3/10 = (9-3)/10 = 6/10
• 7/9 - 2/9 - 1/9 = (7-2-1)/9 = 4/9

Podobnie jak przy dodawaniu, sprawdźcie, czy po odjęciu ułamek można skrócić. W przykładzie 6/10, zarówno 6, jak i 10 można podzielić przez 2. Zatem:

6/10 = (6:2) / (10:2) = 3/5

Dodawanie i odejmowanie ułamków o różnych mianownikach

Sprawa się trochę komplikuje, kiedy ułamki mają różne mianowniki. Nie możemy po prostu dodać lub odjąć liczników, ponieważ ułamki reprezentują części podzielone na różne ilości. Musimy najpierw sprowadzić ułamki do wspólnego mianownika.

Co to znaczy "sprowadzić do wspólnego mianownika"? To znaczy znaleźć taki mianownik, który będzie pasował do obu ułamków. Innymi słowy, musimy znaleźć liczbę, która dzieli się zarówno przez mianownik pierwszego ułamka, jak i przez mianownik drugiego ułamka. Najłatwiej jest znaleźć najmniejszą wspólną wielokrotność (NWW) mianowników.

Przykład: 1/2 + 1/3

Mianowniki to 2 i 3. Musimy znaleźć NWW liczb 2 i 3. W tym przypadku NWW to 6 (ponieważ 6 dzieli się zarówno przez 2, jak i przez 3).

Teraz musimy zamienić ułamki tak, aby miały mianownik 6.

• Żeby zamienić 1/2 na ułamek o mianowniku 6, musimy pomnożyć zarówno licznik, jak i mianownik przez 3 (bo 2 * 3 = 6). Zatem 1/2 = (13) / (23) = 3/6
• Żeby zamienić 1/3 na ułamek o mianowniku 6, musimy pomnożyć zarówno licznik, jak i mianownik przez 2 (bo 3 * 2 = 6). Zatem 1/3 = (12) / (32) = 2/6

Teraz możemy dodać ułamki:

3/6 + 2/6 = (3+2)/6 = 5/6

Przykład odejmowania: 3/4 - 1/6

Mianowniki to 4 i 6. Musimy znaleźć NWW liczb 4 i 6. W tym przypadku NWW to 12 (ponieważ 12 dzieli się zarówno przez 4, jak i przez 6).

• Żeby zamienić 3/4 na ułamek o mianowniku 12, musimy pomnożyć zarówno licznik, jak i mianownik przez 3 (bo 4 * 3 = 12). Zatem 3/4 = (33) / (43) = 9/12
• Żeby zamienić 1/6 na ułamek o mianowniku 12, musimy pomnożyć zarówno licznik, jak i mianownik przez 2 (bo 6 * 2 = 12). Zatem 1/6 = (12) / (62) = 2/12

Teraz możemy odjąć ułamki:

9/12 - 2/12 = (9-2)/12 = 7/12

Kilka dodatkowych wskazówek

• Zawsze sprawdzajcie, czy ułamki można skrócić po dodaniu lub odjęciu.
• Czasami zamiast NWW łatwiej jest pomnożyć mianowniki przez siebie. Wtedy jednak ułamek wynikowy może być trudniejszy do skrócenia. Na przykład, dla 1/2 + 1/3, zamiast szukać NWW (6), można pomnożyć mianowniki 2 * 3 = 6. W tym przypadku wynik będzie taki sam, ale przy bardziej skomplikowanych ułamkach, szukanie NWW jest bardziej efektywne.
• Jeśli macie więcej niż dwa ułamki do dodania lub odjęcia, sprowadźcie je wszystkie do wspólnego mianownika.
• Pamiętajcie o kolejności wykonywania działań, jeśli macie zarówno dodawanie, jak i odejmowanie ułamków.
• Ćwiczcie! Im więcej zadań zrobicie, tym łatwiej będzie Wam dodawać i odejmować ułamki.

Mam nadzieję, że to wyjaśnienie pomoże Wam zrozumieć, jak dodawać i odejmować ułamki zwykłe. Jeśli macie jakieś pytania, śmiało pytajcie! Powodzenia!