Dodawanie I Odejmowanie Ułamków Zwykłych I Dziesiętnych

Dzień dobry wszystkim! Widzę, że macie pytania dotyczące dodawania i odejmowania ułamków, zarówno zwykłych, jak i dziesiętnych. To bardzo ważny temat, który pojawia się na każdym etapie edukacji matematycznej, więc postaram się wyjaśnić wszystko krok po kroku w sposób prosty i zrozumiały.

Zacznijmy od ułamków zwykłych.

Dodawanie i Odejmowanie Ułamków Zwykłych

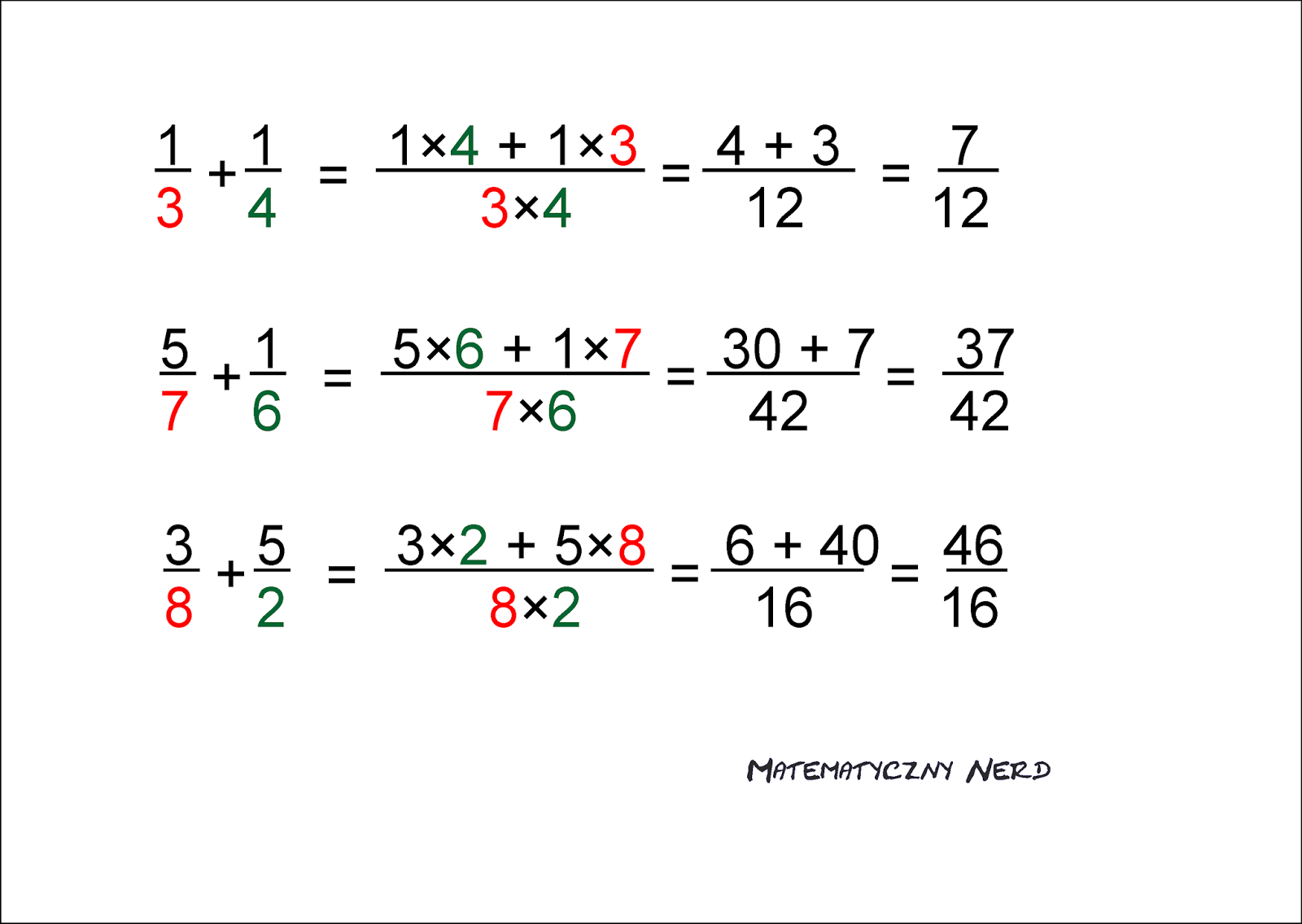
Najważniejsza zasada dodawania i odejmowania ułamków zwykłych brzmi: musimy mieć wspólny mianownik. Co to znaczy? Mianownik to liczba na dole ułamka, ta pod kreską ułamkową. Jeśli mamy dwa ułamki z różnymi mianownikami, to przed dodaniem lub odjęciem musimy je sprowadzić do wspólnego mianownika.

Jak to zrobić? Poszukujemy najmniejszej wspólnej wielokrotności (NWW) mianowników. NWW to najmniejsza liczba, która dzieli się bez reszty przez oba mianowniki.

Przykład 1: Dodajmy ułamki 1/2 i 1/4.

Mamy ułamki 1/2 i 1/4. Mianowniki to 2 i 4. Szukamy NWW liczb 2 i 4. Najmniejsza liczba, która dzieli się zarówno przez 2, jak i przez 4 to 4. Zatem wspólnym mianownikiem będzie 4.

Ułamek 1/2 musimy "rozszerzyć" do ułamka o mianowniku 4. Żeby z 2 zrobić 4, musimy pomnożyć 2 przez 2. Tak samo musimy pomnożyć licznik (górną liczbę) ułamka 1/2 przez 2.

Czyli 1/2 = (1 * 2) / (2 * 2) = 2/4

Teraz mamy: 2/4 + 1/4. Skoro mamy wspólny mianownik, dodajemy liczniki, a mianownik przepisujemy bez zmian.

2/4 + 1/4 = (2 + 1) / 4 = 3/4

Wynik to 3/4.

Przykład 2: Odejmijmy ułamki 3/5 i 1/10.

Mamy ułamki 3/5 i 1/10. Mianowniki to 5 i 10. Szukamy NWW liczb 5 i 10. Najmniejsza liczba, która dzieli się zarówno przez 5, jak i przez 10 to 10. Zatem wspólnym mianownikiem będzie 10.

Ułamek 3/5 musimy rozszerzyć do ułamka o mianowniku 10. Żeby z 5 zrobić 10, musimy pomnożyć 5 przez 2. Tak samo musimy pomnożyć licznik ułamka 3/5 przez 2.

Czyli 3/5 = (3 * 2) / (5 * 2) = 6/10

Teraz mamy: 6/10 - 1/10. Skoro mamy wspólny mianownik, odejmujemy liczniki, a mianownik przepisujemy bez zmian.

6/10 - 1/10 = (6 - 1) / 10 = 5/10

Wynik to 5/10. Zauważcie, że ułamek 5/10 można jeszcze skrócić, dzieląc licznik i mianownik przez 5.

5/10 = (5 : 5) / (10 : 5) = 1/2

Ostateczny wynik to 1/2.

Przykład 3: Dodajmy ułamki 2/3 i 1/4.

Mamy ułamki 2/3 i 1/4. Mianowniki to 3 i 4. Szukamy NWW liczb 3 i 4. Najmniejsza liczba, która dzieli się zarówno przez 3, jak i przez 4 to 12. Zatem wspólnym mianownikiem będzie 12.

Ułamek 2/3 musimy rozszerzyć do ułamka o mianowniku 12. Żeby z 3 zrobić 12, musimy pomnożyć 3 przez 4. Tak samo musimy pomnożyć licznik ułamka 2/3 przez 4.

Czyli 2/3 = (2 * 4) / (3 * 4) = 8/12

Ułamek 1/4 musimy rozszerzyć do ułamka o mianowniku 12. Żeby z 4 zrobić 12, musimy pomnożyć 4 przez 3. Tak samo musimy pomnożyć licznik ułamka 1/4 przez 3.

Czyli 1/4 = (1 * 3) / (4 * 3) = 3/12

Teraz mamy: 8/12 + 3/12. Skoro mamy wspólny mianownik, dodajemy liczniki, a mianownik przepisujemy bez zmian.

8/12 + 3/12 = (8 + 3) / 12 = 11/12

Wynik to 11/12.

Co, jeśli mamy ułamki mieszane? To ułamki, które mają część całkowitą (np. 2 1/3). Przed dodawaniem lub odejmowaniem, zamieniamy ułamki mieszane na ułamki niewłaściwe. Jak to zrobić?

Żeby zamienić ułamek mieszany na niewłaściwy, mnożymy mianownik przez część całkowitą, dodajemy licznik, a mianownik przepisujemy bez zmian.

Przykład: Zamieńmy 2 1/3 na ułamek niewłaściwy.

Mianownik to 3, część całkowita to 2, licznik to 1.

(3 * 2 + 1) / 3 = (6 + 1) / 3 = 7/3

Czyli 2 1/3 = 7/3

Po zamianie ułamków mieszanych na niewłaściwe, postępujemy tak samo, jak w przypadku zwykłych ułamków – sprowadzamy do wspólnego mianownika i dodajemy lub odejmujemy liczniki.

Dodawanie i Odejmowanie Ułamków Dziesiętnych

Dodawanie i odejmowanie ułamków dziesiętnych jest dużo prostsze, o ile pamiętamy o jednej bardzo ważnej rzeczy: przecinek pod przecinkiem!

Układamy ułamki w słupku tak, żeby przecinki były jeden pod drugim. Następnie dodajemy lub odejmujemy, tak jak normalne liczby. Jeśli brakuje nam cyfr po przecinku, możemy dopisać zera, to nie zmienia wartości ułamka.

Przykład 1: Dodajmy ułamki 2,5 i 1,3.

  2,5
+ 1,3
-------
  3,8

Przecinek pod przecinkiem, dodajemy normalnie. Wynik to 3,8.

Przykład 2: Dodajmy ułamki 3,14 i 0,7.

  3,14
+ 0,70  (dopisaliśmy zero, żeby mieć tyle samo cyfr po przecinku)
-------
  3,84

Przecinek pod przecinkiem, dodajemy normalnie. Wynik to 3,84.

Przykład 3: Odejmijmy ułamki 5,7 i 2,1.

  5,7
- 2,1
-------
  3,6

Przecinek pod przecinkiem, odejmujemy normalnie. Wynik to 3,6.

Przykład 4: Odejmijmy ułamki 4,2 i 1,85.

  4,20 (dopisaliśmy zero, żeby móc odjąć)
- 1,85
-------
  2,35

Przecinek pod przecinkiem, odejmujemy normalnie. Trzeba pamiętać o pożyczaniu! Wynik to 2,35.

Co zrobić, jeśli mamy liczby całkowite i ułamki dziesiętne? Na przykład 5 + 2,3? Liczbę całkowitą możemy zapisać jako ułamek dziesiętny z przecinkiem i zerami: 5 = 5,0. Wtedy układamy w słupku i dodajemy:

  5,0
+ 2,3
-------
  7,3

Podobnie z odejmowaniem.

Ułamki Zwykłe i Dziesiętne – Przechodzenie między Nimi

Czasami potrzebujemy zamienić ułamek zwykły na dziesiętny, albo odwrotnie.

Z ułamka zwykłego na dziesiętny: Najprościej jest podzielić licznik przez mianownik. Można to zrobić pisemnie lub za pomocą kalkulatora.

Przykład: Zamieńmy ułamek 1/4 na dziesiętny.

Dzielimy 1 przez 4: 1 : 4 = 0,25

Zatem 1/4 = 0,25

Przykład: Zamieńmy ułamek 3/8 na dziesiętny.

Dzielimy 3 przez 8: 3 : 8 = 0,375

Zatem 3/8 = 0,375

Z ułamka dziesiętnego na zwykły: Zapisujemy ułamek dziesiętny jako ułamek zwykły o mianowniku 10, 100, 1000, itd., w zależności od tego, ile mamy cyfr po przecinku. Następnie skracamy ułamek, jeśli to możliwe.

Przykład: Zamieńmy ułamek 0,5 na zwykły.

0,5 = 5/10 (jedna cyfra po przecinku, więc mianownik to 10)

Skracamy ułamek 5/10, dzieląc licznik i mianownik przez 5: 5/10 = 1/2

Zatem 0,5 = 1/2

Przykład: Zamieńmy ułamek 0,75 na zwykły.

0,75 = 75/100 (dwie cyfry po przecinku, więc mianownik to 100)

Skracamy ułamek 75/100. Możemy podzielić licznik i mianownik przez 25: 75/100 = 3/4

Zatem 0,75 = 3/4

Mam nadzieję, że to wyjaśnienie było pomocne. Ćwiczcie, rozwiązujcie zadania, a ułamki przestaną być dla Was tajemnicą! Pamiętajcie – regularna praktyka czyni mistrza! Powodzenia!