Dodawanie I Odejmowanie Ułamków O Tych Samych Mianownikach Klasa 5

Dobrze, posłuchajcie uważnie, bo temat dodawania i odejmowania ułamków o tych samych mianownikach w klasie 5 to fundament, który musicie opanować do perfekcji. Bez tego ani rusz dalej!

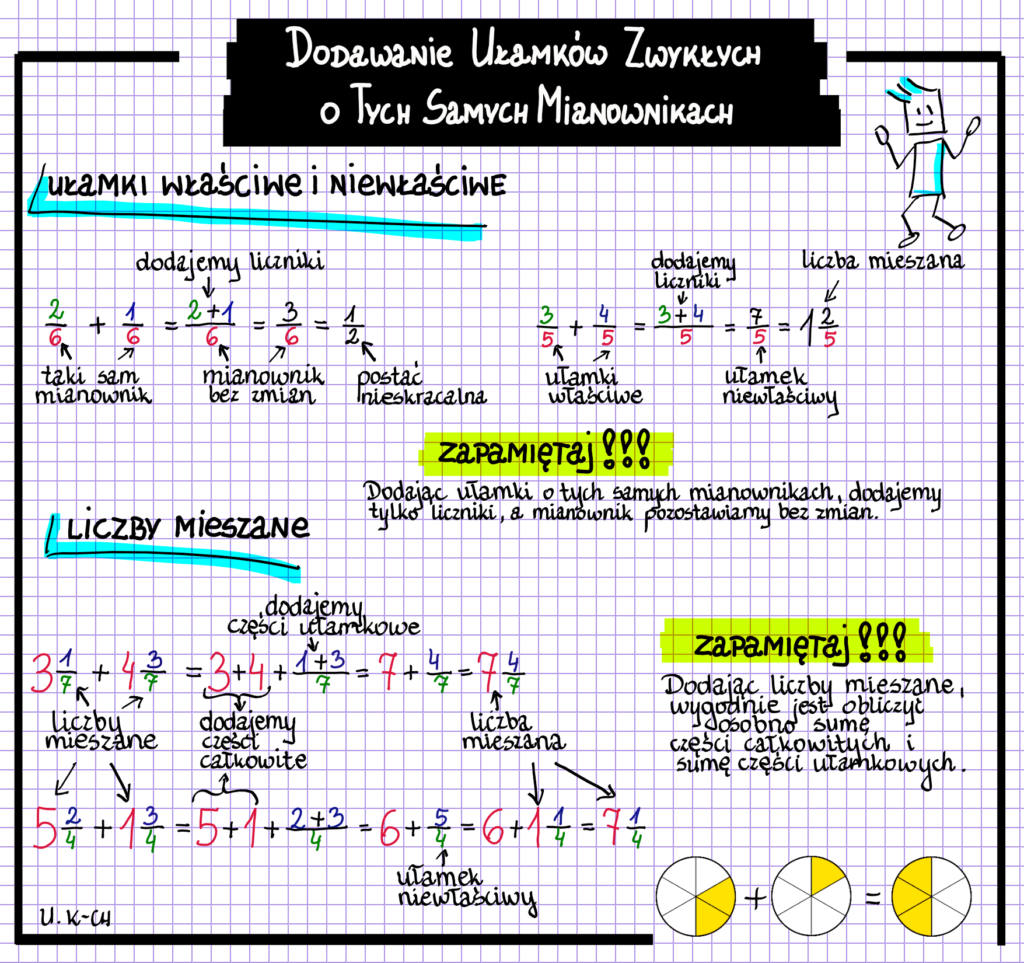
Zaczniemy od najprostszych przypadków. Jeżeli mamy dodać dwa ułamki, na przykład 3/7 i 2/7, to sprawdzamy, czy mianowniki są takie same. W tym przypadku są. Więc przepisujemy mianownik, czyli 7, a dodajemy tylko liczniki: 3 + 2 = 5. Wynik to 5/7.

Podobnie z odejmowaniem. Jeśli mamy 5/9 - 2/9, to mianownik (9) przepisujemy, a odejmujemy liczniki: 5 - 2 = 3. Wynik to 3/9. Pamiętajcie, że wynik zawsze sprawdzamy, czy da się go skrócić. W tym przypadku 3/9 można skrócić przez 3, otrzymując 1/3. Zawsze dążymy do przedstawienia ułamka w najprostszej postaci.

Teraz trochę trudniejsze przykłady. Załóżmy, że mamy 11/15 + 2/15 + 1/15. Mianownik jest wspólny (15), więc przepisujemy go. Dodajemy liczniki: 11 + 2 + 1 = 14. Wynik to 14/15. Tym razem nie da się skrócić.

A co, jeśli mamy odejmowanie z kilkoma ułamkami? Na przykład 9/11 - 3/11 - 1/11. Mianownik (11) zostaje. Odejmujemy liczniki po kolei: 9 - 3 - 1 = 5. Wynik to 5/11. Znów, nie można skrócić.

Pamiętajcie, kolejność wykonywania działań jest ważna. Jeżeli mamy wyrażenie typu 12/17 - 5/17 + 2/17, to wykonujemy odejmowanie, a potem dodawanie, chyba że są nawiasy. Czyli najpierw 12 - 5 = 7, a potem 7 + 2 = 9. Wynik to 9/17.

Jeśli mamy ułamek niewłaściwy w wyniku, na przykład 15/7, to zamieniamy go na liczbę mieszaną. W 15 mieści się 2 siódemki (2 * 7 = 14), a reszta to 1. Zatem 15/7 to 2 i 1/7. To bardzo ważne, żeby umieć zamieniać ułamki niewłaściwe na liczby mieszane i odwrotnie.

A co z zadaniami tekstowymi? Załóżmy, że Kasia zjadła 2/5 tortu, a Tomek 1/5 tortu. Ile tortu zjedli razem? Mamy dodawanie: 2/5 + 1/5 = 3/5. Odpowiedź: Razem zjedli 3/5 tortu.

Inny przykład: Mama upiekła 7/8 ciasta. Zjedliśmy 3/8 ciasta. Ile ciasta zostało? Mamy odejmowanie: 7/8 - 3/8 = 4/8. Możemy skrócić 4/8 przez 4, otrzymując 1/2. Odpowiedź: Zostało 1/2 ciasta.

I jeszcze jedno: W klasie 5a jest 10/25 uczniów, którzy lubią matematykę, a w klasie 5b jest 8/25 uczniów, którzy lubią matematykę. Jaka część wszystkich uczniów klas piątych lubi matematykę (zakładając, że obie klasy są tej samej wielkości)? Dodajemy: 10/25 + 8/25 = 18/25. Odpowiedź: 18/25 uczniów lubi matematykę.

Zauważcie, że kluczem jest zawsze wspólny mianownik. Bez tego ani rusz. Jeśli macie ułamki o różnych mianownikach (co zobaczycie w przyszłości), musicie je sprowadzić do wspólnego mianownika. Ale to już inna historia.

Pamiętajcie o skracaniu ułamków. Zawsze, gdy to możliwe, doprowadzajcie ułamek do najprostszej postaci. To świadczy o waszej biegłości w operacjach na ułamkach.

Bardziej Złożone Przykłady

Teraz przejdźmy do przykładów, które wymagają nieco więcej uwagi. Wyobraźmy sobie sytuację, gdzie mamy więcej niż dwa działania i liczby mieszane do tego:

Przykład 1: Oblicz 3 i 2/11 + 1 i 5/11 - 2/11.

Najpierw skupiamy się na całościach. Mamy 3 + 1 = 4. Teraz dodajemy ułamki: 2/11 + 5/11 = 7/11. Następnie odejmujemy 2/11, czyli 7/11 - 2/11 = 5/11. Czyli wynik to 4 i 5/11.

Przykład 2: Oblicz 7/13 - 2/13 + 1 i 6/13.

Tutaj najpierw zajmujemy się ułamkami: 7/13 - 2/13 = 5/13. Następnie dodajemy do tego liczbę mieszaną, czyli 5/13 + 6/13 = 11/13. Do tego mamy całą liczbę 1 z liczby mieszanej. Więc wynik to 1 i 11/13.

Przykład 3: Co się stanie, jeśli odejmowanie ułamków da nam wynik ujemny w liczbie mieszanej? Załóżmy, że mamy 2 i 1/5 - 3/5. Musimy "pożyczyć" jedną całą liczbę od 2, zamieniając ją na 5/5. Wtedy mamy 1 i 6/5 - 3/5. Teraz możemy odjąć: 6/5 - 3/5 = 3/5. Wynik to 1 i 3/5.

Widzicie, że manipulacja liczbami mieszanymi wymaga trochę więcej wprawy. Trzeba pamiętać o zamianie całości na ułamki i o "pożyczaniu", jeśli zachodzi taka potrzeba.

Pułapki i Częste Błędy

Muszę was przestrzec przed typowymi błędami, które zdarzają się uczniom:

Dodawanie/odejmowanie zarówno liczników, jak i mianowników: To absolutnie niedopuszczalne! Mianownik pozostaje bez zmian, jeśli jest wspólny. Dodajemy lub odejmujemy tylko liczniki.
Zapominanie o skracaniu ułamków: Zawsze upraszczajcie wynik do najprostszej postaci. To pokazuje, że rozumiecie, co robicie.
Problemy z liczbami mieszanymi: Upewnijcie się, że potraficie sprawnie zamieniać liczby mieszane na ułamki niewłaściwe i odwrotnie. To kluczowe w bardziej skomplikowanych obliczeniach.
Brak uwagi na kolejność działań: Jeśli macie więcej niż jedno działanie, wykonujcie je po kolei, chyba że są nawiasy.

Ćwiczenia i Powtórka

Teraz czas na ćwiczenia. Im więcej rozwiążecie zadań, tym lepiej utrwalicie sobie tę wiedzę. Poproście mnie o dodatkowe zadania, jeśli czujecie, że potrzebujecie więcej praktyki.

Pamiętajcie, że opanowanie dodawania i odejmowania ułamków o tych samych mianownikach to podstawa do dalszej nauki o ułamkach. Nie lekceważcie tego!

I jeszcze jedno: regularnie powtarzajcie materiał. Matematyka to nie wkuwanie na pamięć, tylko zrozumienie zasad i ćwiczenie. Tylko wtedy będziecie czuli się pewnie i swobodnie z ułamkami. Jeśli macie jakieś pytania, nie krępujcie się pytać. Jestem tu, żeby wam pomóc!