Dodawanie I Odejmowanie Ułamków O Tych Samych Mianownikach

Dodawanie i odejmowanie ułamków o tych samych mianownikach to jedna z podstawowych operacji w arytmetyce ułamków. Jest to prostsze niż dodawanie i odejmowanie ułamków o różnych mianownikach, ponieważ nie wymaga sprowadzania ich do wspólnego mianownika. Zamiast tego, skupiamy się bezpośrednio na licznikach, utrzymując mianownik bez zmian.

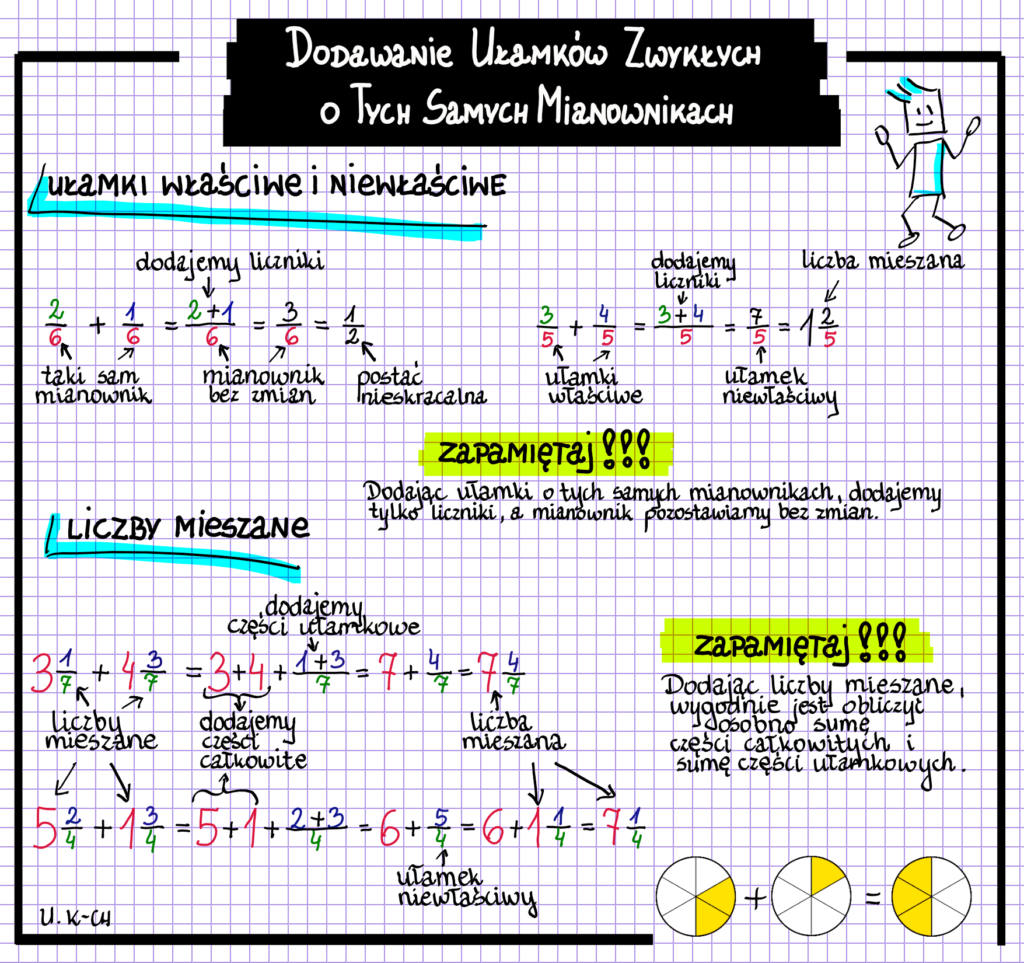
Żeby dodać ułamki o tych samych mianownikach, dodajemy po prostu ich liczniki, a mianownik pozostaje ten sam. Przykładowo, jeżeli mamy ułamki 2/5 i 1/5, dodajemy liczniki (2 + 1 = 3), a mianownik pozostaje 5. Wynikiem jest ułamek 3/5. To bardzo proste! Możemy to zapisać w następujący sposób: a/c + b/c = (a + b)/c. Ta zasada obowiązuje dla dowolnej liczby ułamków o tym samym mianowniku. Możemy dodawać trzy, cztery, a nawet więcej ułamków, o ile wszystkie mają ten sam mianownik. Weźmy na przykład 1/7 + 2/7 + 3/7. Dodajemy liczniki: 1 + 2 + 3 = 6. Mianownik pozostaje bez zmian, czyli 7. Wynikiem jest ułamek 6/7.

Podobnie, aby odjąć ułamki o tych samych mianownikach, odejmujemy ich liczniki, a mianownik pozostaje ten sam. Na przykład, jeżeli mamy ułamki 5/8 i 2/8, odejmujemy liczniki (5 - 2 = 3), a mianownik pozostaje 8. Wynikiem jest ułamek 3/8. Możemy to zapisać jako: a/c - b/c = (a - b)/c. Istotne jest, żeby pamiętać o kolejności odejmowania. Odejmujemy drugi licznik od pierwszego, a nie odwrotnie, chyba że mamy do czynienia z liczbami ujemnymi. Spójrzmy na przykład 9/11 - 4/11. Odejmujemy 4 od 9, co daje nam 5. Mianownik pozostaje 11. Wynikiem jest 5/11.

Ważne jest, żeby pamiętać, że wynik dodawania lub odejmowania ułamków powinien być zawsze uproszczony, jeżeli to możliwe. Oznacza to, że powinniśmy znaleźć największy wspólny dzielnik licznika i mianownika i podzielić przez niego oba te elementy ułamka. Na przykład, jeżeli po dodaniu lub odjęciu otrzymamy ułamek 4/6, możemy go uprościć, dzieląc zarówno licznik, jak i mianownik przez 2. Otrzymamy wtedy ułamek 2/3.

Kiedy pracujemy z liczbami mieszanymi, najpierw możemy zamienić je na ułamki niewłaściwe, a następnie dodać lub odjąć ułamki, stosując opisane powyżej zasady. Liczba mieszana składa się z liczby całkowitej i ułamka właściwego (czyli ułamka, w którym licznik jest mniejszy od mianownika). Na przykład, 2 1/3 to liczba mieszana. Aby zamienić ją na ułamek niewłaściwy, mnożymy liczbę całkowitą (2) przez mianownik (3), a następnie dodajemy licznik (1). Otrzymujemy 2 * 3 + 1 = 7. Mianownik pozostaje ten sam, czyli 3. Zatem 2 1/3 = 7/3.

Przykłady dodawania i odejmowania ułamków

Rozważmy kilka przykładów, żeby utrwalić wiedzę.

1. Dodawanie: 3/10 + 5/10. Liczniki dodajemy: 3 + 5 = 8. Mianownik pozostaje 10. Wynik to 8/10. Możemy uprościć ten ułamek, dzieląc licznik i mianownik przez 2, co daje nam 4/5.

2. Dodawanie większej liczby ułamków: 1/4 + 2/4 + 1/4. Liczniki dodajemy: 1 + 2 + 1 = 4. Mianownik pozostaje 4. Wynik to 4/4. Ponieważ licznik i mianownik są równe, ułamek ten jest równy 1.

3. Odejmowanie: 7/9 - 2/9. Odejmujemy liczniki: 7 - 2 = 5. Mianownik pozostaje 9. Wynik to 5/9.

4. Odejmowanie z liczbami mieszanymi: Załóżmy, że mamy obliczyć 3 2/5 - 1 1/5. Najpierw zamieniamy liczby mieszane na ułamki niewłaściwe: 3 2/5 = (3 * 5 + 2)/5 = 17/5 oraz 1 1/5 = (1 * 5 + 1)/5 = 6/5. Teraz odejmujemy ułamki: 17/5 - 6/5 = (17 - 6)/5 = 11/5. Możemy zamienić ten ułamek niewłaściwy z powrotem na liczbę mieszaną: 11/5 = 2 1/5.

5. Dodawanie z liczbami mieszanymi: Załóżmy, że mamy obliczyć 2 3/7 + 1 2/7. Najpierw zamieniamy liczby mieszane na ułamki niewłaściwe: 2 3/7 = (2 * 7 + 3)/7 = 17/7 oraz 1 2/7 = (1 * 7 + 2)/7 = 9/7. Teraz dodajemy ułamki: 17/7 + 9/7 = (17 + 9)/7 = 26/7. Możemy zamienić ten ułamek niewłaściwy z powrotem na liczbę mieszaną: 26/7 = 3 5/7.

Ćwiczenia

Aby jeszcze lepiej opanować dodawanie i odejmowanie ułamków o tych samych mianownikach, warto rozwiązać kilka prostych ćwiczeń. Spróbuj obliczyć następujące wyrażenia:

1. 2/11 + 5/11
2. 7/15 - 3/15
3. 1/8 + 3/8 + 2/8
4. 4/5 - 1/5
5. 2 1/4 + 1 2/4
6. 3 5/9 - 1 2/9

Pamiętaj o upraszczaniu wyników, jeśli to możliwe! Rozwiązania do tych ćwiczeń znajdziesz na końcu tego artykułu.

Dodawanie i odejmowanie ułamków o tych samych mianownikach to fundament do bardziej skomplikowanych operacji na ułamkach. Zrozumienie tej prostej zasady pozwala na łatwiejsze radzenie sobie z bardziej zaawansowanymi problemami matematycznymi. Ćwicz regularnie, a dodawanie i odejmowanie ułamków stanie się dla Ciebie drugą naturą! Pamiętaj, że matematyka wymaga praktyki, a im więcej ćwiczysz, tym lepiej rozumiesz zasady i tym szybciej rozwiązujesz zadania. Nie zrażaj się początkowymi trudnościami – każdy kiedyś zaczynał. Konsekwencja i regularne ćwiczenia to klucz do sukcesu w matematyce.

Odpowiedzi do ćwiczeń:

1. 7/11
2. 4/15
3. 6/8 = 3/4
4. 3/5
5. 3 3/4
6. 2 3/9 = 2 1/3