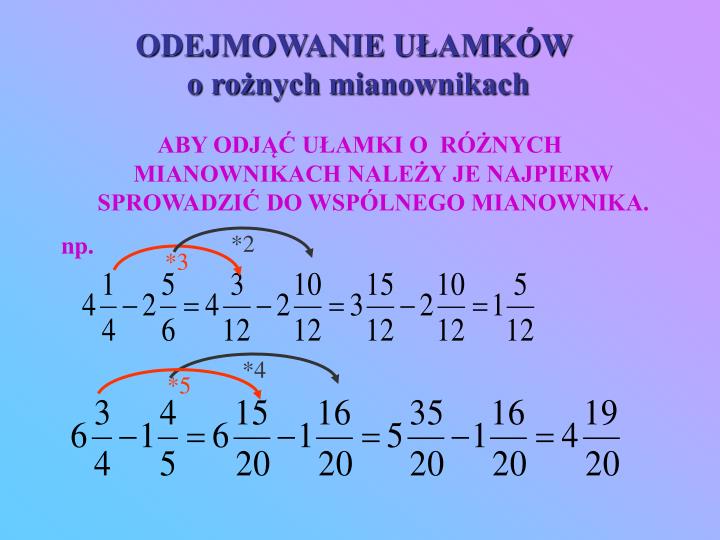
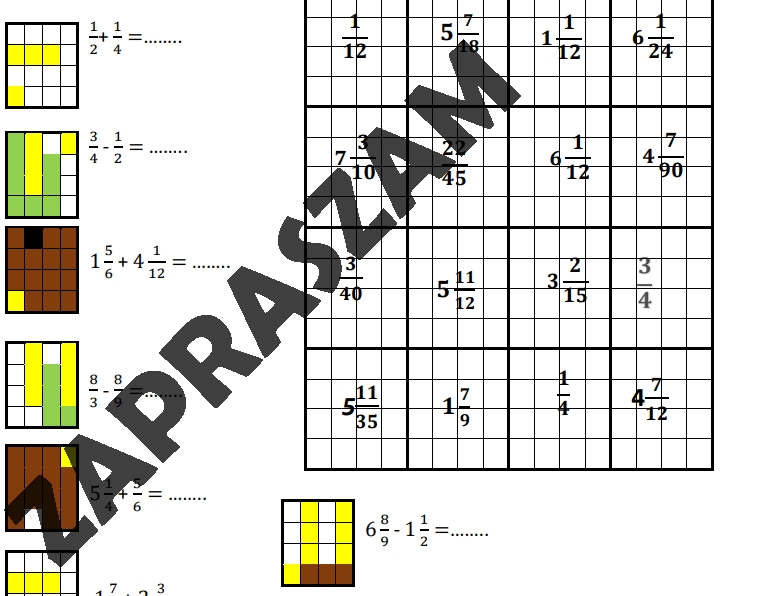
Dodawanie I Odejmowanie Ułamków O Różnych Mianownikach Pdf

Dzień dobry wszystkim! Dzisiaj zajmiemy się dodawaniem i odejmowaniem ułamków o różnych mianownikach. Wiem, że to czasem sprawia trudności, ale obiecuję, że po dzisiejszej lekcji stanie się to o wiele prostsze. Przygotujcie się na solidną dawkę przykładów i ćwiczeń!
Zaczynamy!
Kluczem do sukcesu w dodawaniu i odejmowaniu ułamków o różnych mianownikach jest sprowadzenie ich do wspólnego mianownika. Co to znaczy? To znaczy, że musimy znaleźć taką liczbę, która będzie podzielna przez oba mianowniki.
Przykład 1: Dodawanie ułamków
Załóżmy, że mamy do dodania ułamki 1/2 i 1/3. Mianowniki to 2 i 3. Jak znaleźć wspólny mianownik? Możemy wypisać wielokrotności każdej z tych liczb:
- Wielokrotności liczby 2: 2, 4, 6, 8, 10, 12...
- Wielokrotności liczby 3: 3, 6, 9, 12, 15...
Widzimy, że zarówno 6, jak i 12 pojawiają się w obu zestawieniach. Możemy użyć 6 jako wspólnego mianownika (jest mniejsza, więc łatwiej będzie nam liczyć).
Teraz musimy zamienić ułamki 1/2 i 1/3 tak, aby miały mianownik 6.
- Aby zamienić 1/2 na ułamek o mianowniku 6, musimy pomnożyć zarówno licznik, jak i mianownik przez 3 (ponieważ 2 * 3 = 6). Zatem 1/2 = (1 * 3) / (2 * 3) = 3/6.
- Aby zamienić 1/3 na ułamek o mianowniku 6, musimy pomnożyć zarówno licznik, jak i mianownik przez 2 (ponieważ 3 * 2 = 6). Zatem 1/3 = (1 * 2) / (3 * 2) = 2/6.
Teraz możemy dodać ułamki: 3/6 + 2/6 = 5/6.
Gotowe! 1/2 + 1/3 = 5/6.
Przykład 2: Odejmowanie ułamków
Spróbujmy teraz odjąć od siebie ułamki 3/4 i 1/5. Mamy mianowniki 4 i 5. Znów wypisujemy wielokrotności:
- Wielokrotności liczby 4: 4, 8, 12, 16, 20, 24...
- Wielokrotności liczby 5: 5, 10, 15, 20, 25...
Wspólny mianownik to 20.
- Aby zamienić 3/4 na ułamek o mianowniku 20, mnożymy licznik i mianownik przez 5 (ponieważ 4 * 5 = 20). Zatem 3/4 = (3 * 5) / (4 * 5) = 15/20.
- Aby zamienić 1/5 na ułamek o mianowniku 20, mnożymy licznik i mianownik przez 4 (ponieważ 5 * 4 = 20). Zatem 1/5 = (1 * 4) / (5 * 4) = 4/20.
Teraz odejmujemy: 15/20 - 4/20 = 11/20.
Czyli 3/4 - 1/5 = 11/20.
Znajdowanie Najmniejszej Wspólnej Wielokrotności (NWW)
W przykładach wypisywaliśmy wielokrotności, żeby znaleźć wspólny mianownik. Jest na to szybszy sposób – znaleźć Najmniejszą Wspólną Wielokrotność (NWW) mianowników. To najmniejsza liczba, która dzieli się przez oba mianowniki. Czasami od razu ją widzimy, a czasem musimy trochę pokombinować.
Przykład 3: Użycie NWW
Mamy ułamki 5/12 i 7/18. Znalezienie NWW 12 i 18 może być trudniejsze niż wcześniej. Możemy użyć rozkładu na czynniki pierwsze:
- 12 = 2 * 2 * 3
- 18 = 2 * 3 * 3
NWW to iloczyn wszystkich czynników pierwszych, wziętych z największą potęgą, w jakiej występują w obu rozkładach. Czyli NWW(12, 18) = 2 * 2 * 3 * 3 = 36.
Teraz zamieniamy ułamki na te o mianowniku 36:
- Aby zamienić 5/12 na ułamek o mianowniku 36, mnożymy licznik i mianownik przez 3 (ponieważ 12 * 3 = 36). Zatem 5/12 = (5 * 3) / (12 * 3) = 15/36.
- Aby zamienić 7/18 na ułamek o mianowniku 36, mnożymy licznik i mianownik przez 2 (ponieważ 18 * 2 = 36). Zatem 7/18 = (7 * 2) / (18 * 2) = 14/36.
Możemy na przykład je dodać: 15/36 + 14/36 = 29/36.
Ułamki mieszane
A co jeśli mamy ułamki mieszane, np. 1 1/2 + 2 1/4?
Najprościej jest zamienić ułamki mieszane na ułamki niewłaściwe, a potem postępować jak wcześniej.
- 1 1/2 = (1 * 2 + 1) / 2 = 3/2
- 2 1/4 = (2 * 4 + 1) / 4 = 9/4
Teraz szukamy wspólnego mianownika dla 2 i 4. To oczywiście 4.
- 3/2 = (3 * 2) / (2 * 2) = 6/4
Dodajemy: 6/4 + 9/4 = 15/4.
Możemy zamienić z powrotem na ułamek mieszany: 15/4 = 3 3/4.
Podsumowanie najważniejszych kroków
- Znajdź wspólny mianownik (najlepiej NWW) dla wszystkich ułamków.
- Zamień każdy ułamek na ułamek o wspólnym mianowniku, mnożąc licznik i mianownik przez odpowiednią liczbę.
- Dodaj lub odejmij liczniki, zachowując wspólny mianownik.
- Uprość wynik, jeśli to możliwe (czyli skróć ułamek, jeśli licznik i mianownik mają wspólny dzielnik).
- Jeśli pracujesz z ułamkami mieszanymi, zamień je najpierw na ułamki niewłaściwe. Po obliczeniach możesz zamienić wynik z powrotem na ułamek mieszany.
Kilka dodatkowych przykładów do przećwiczenia:
- 2/5 + 1/10 = ?
- 7/8 - 1/4 = ?
- 1/3 + 2/9 = ?
- 5/6 - 1/3 = ?
- 1 1/3 + 2/3 = ?
- 2 1/2 - 1 1/4 = ?
Rozwiązania:
- 2/5 + 1/10 = 4/10 + 1/10 = 5/10 = 1/2
- 7/8 - 1/4 = 7/8 - 2/8 = 5/8
- 1/3 + 2/9 = 3/9 + 2/9 = 5/9
- 5/6 - 1/3 = 5/6 - 2/6 = 3/6 = 1/2
- 1 1/3 + 2/3 = 4/3 + 2/3 = 6/3 = 2
- 2 1/2 - 1 1/4 = 5/2 - 5/4 = 10/4 - 5/4 = 5/4 = 1 1/4
Mam nadzieję, że to pomogło! Pamiętajcie, praktyka czyni mistrza. Im więcej przykładów rozwiążecie, tym łatwiej będzie Wam dodawać i odejmować ułamki o różnych mianownikach. Powodzenia! Jeśli macie jakieś pytania, śmiało pytajcie.


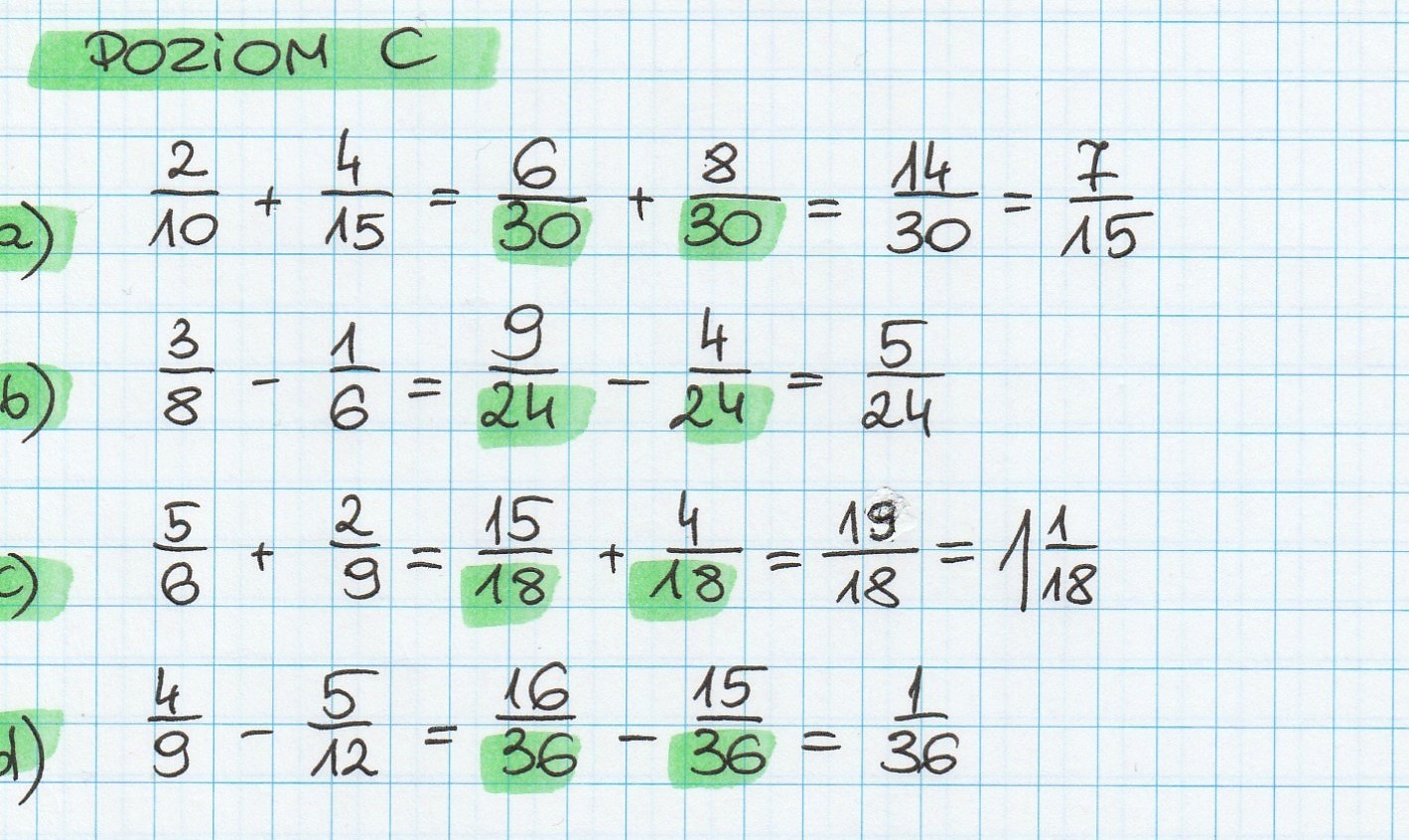
![Dodawanie I Odejmowanie Ułamków O Różnych Mianownikach Pdf [Matematyka, Zadania] Dodawanie ułamków](http://aztekium.pl/__qbase/questions/pl/files/3000/3441.0/[Aztekium.pl]dodawanie dwoch mianowniki rozne ulamkow.jpg)