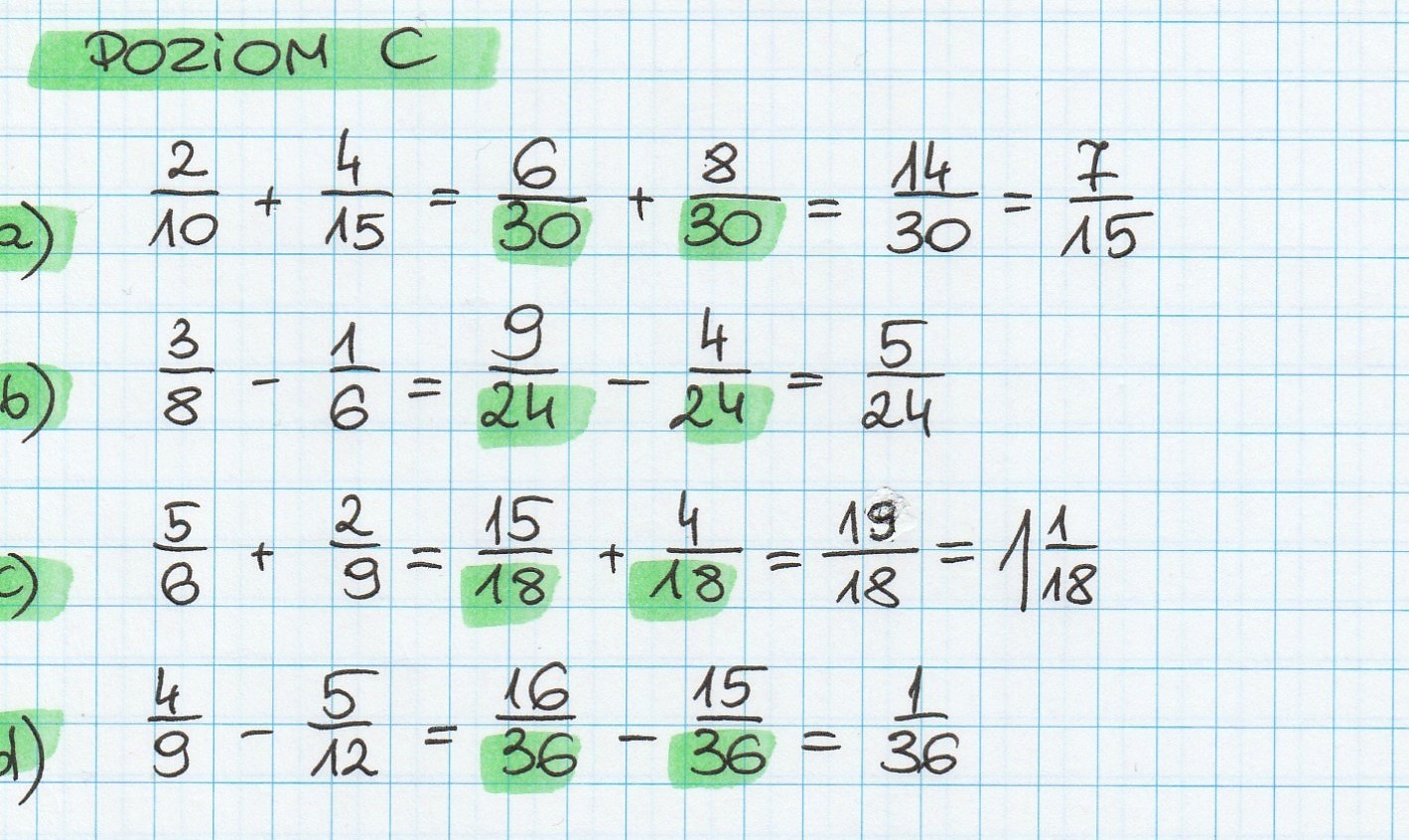Dodawanie I Odejmowanie Ułamków O Różnych Mianownikach Karta Pracy

Dobrze, przygotujmy się do dokładnego omówienia dodawania i odejmowania ułamków o różnych mianownikach, koncentrując się na tym, co jest istotne w kontekście kart pracy.

Dodawanie i odejmowanie ułamków o różnych mianownikach wymaga od nas sprowadzenia tych ułamków do wspólnego mianownika. To jest fundamentalny krok, bez którego poprawne wykonanie działania nie jest możliwe. Mianownik ułamka określa, na ile równych części podzielona jest całość, więc dopóki ułamki nie mają tego samego mianownika, nie możemy ich bezpośrednio dodawać ani odejmować.

Pierwszym etapem jest znalezienie najmniejszego wspólnego mianownika (NWW) dla mianowników ułamków, które chcemy dodać lub odjąć. NWW to najmniejsza liczba, która jest podzielna przez wszystkie mianowniki. Możemy to zrobić na kilka sposobów. Jednym z nich jest wypisanie wielokrotności każdego z mianowników, aż znajdziemy wspólną wielokrotność. Na przykład, jeśli mamy ułamki z mianownikami 4 i 6, wypisujemy:

Wielokrotności 4: 4, 8, 12, 16, 20, 24... Wielokrotności 6: 6, 12, 18, 24, 30...

Widzimy, że 12 jest najmniejszą wspólną wielokrotnością, więc będzie naszym wspólnym mianownikiem.

Inną metodą jest rozkład mianowników na czynniki pierwsze. Rozkładamy każdy mianownik na iloczyn liczb pierwszych. Następnie, aby znaleźć NWW, bierzemy każdy czynnik pierwszy występujący w rozkładach, w największej potędze, w jakiej występuje. Na przykład:

4 = 2 x 2 = 2^2 6 = 2 x 3

NWW(4, 6) = 2^2 x 3 = 4 x 3 = 12

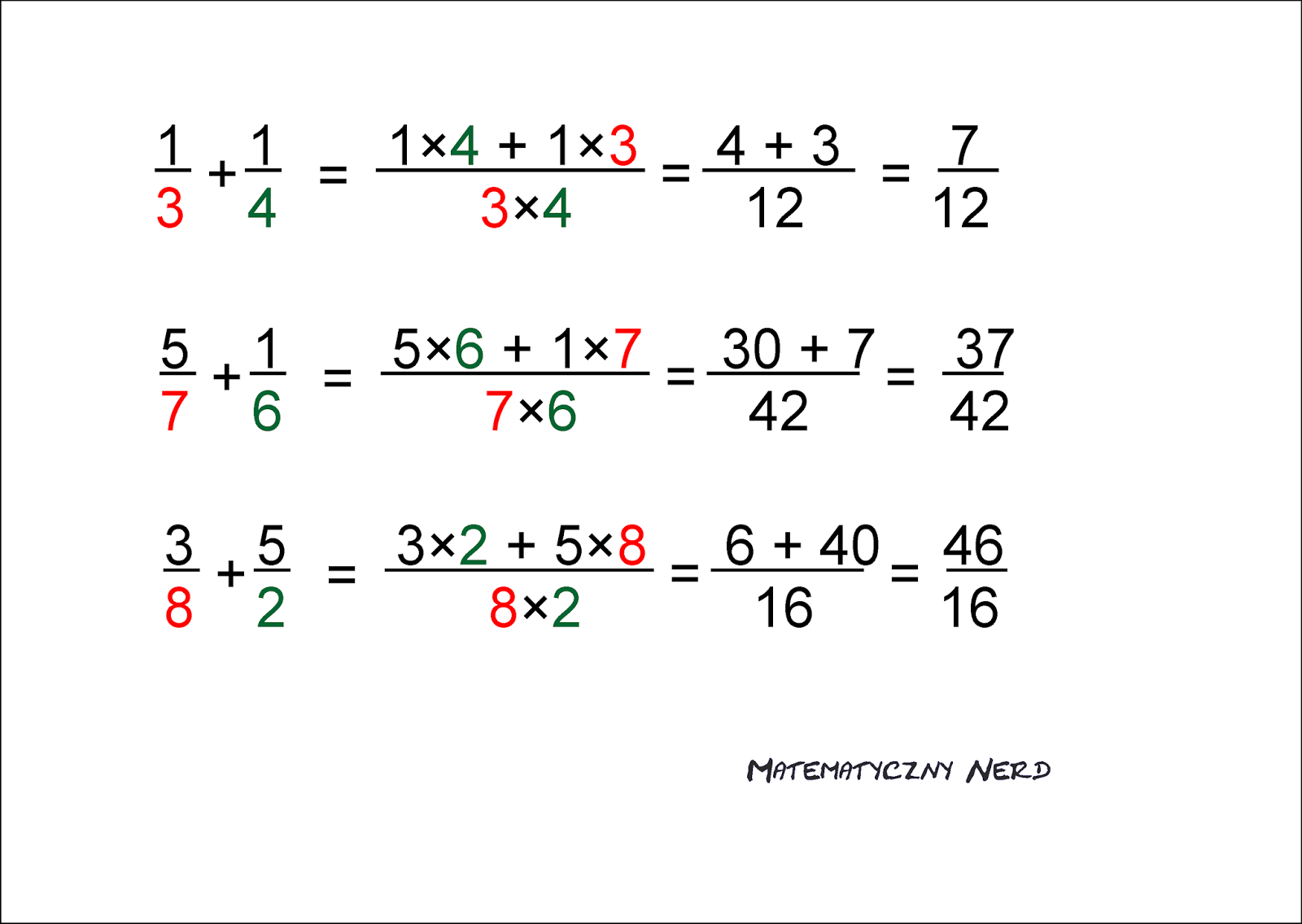
Po znalezieniu NWW, musimy przekształcić każdy ułamek tak, aby miał ten nowy mianownik. Robimy to, mnożąc licznik i mianownik każdego ułamka przez taką liczbę, aby mianownik stał się równy NWW. W naszym przykładzie:

Ułamek z mianownikiem 4: mnożymy licznik i mianownik przez 3 (bo 4 x 3 = 12). Ułamek z mianownikiem 6: mnożymy licznik i mianownik przez 2 (bo 6 x 2 = 12).

Załóżmy, że mamy ułamki 1/4 i 1/6. Po przekształceniu otrzymamy:

(1 x 3) / (4 x 3) = 3/12 (1 x 2) / (6 x 2) = 2/12

Teraz, gdy ułamki mają wspólny mianownik, możemy je dodać lub odjąć, dodając lub odejmując liczniki, a mianownik pozostawiając bez zmian. W naszym przykładzie:

3/12 + 2/12 = (3 + 2) / 12 = 5/12

Odejmując:

3/12 - 2/12 = (3 - 2) / 12 = 1/12

Karta Pracy: Dodatkowe Rozważania

Karty pracy często zawierają różnorodne przykłady, które mają na celu utrwalenie umiejętności. Mogą obejmować:

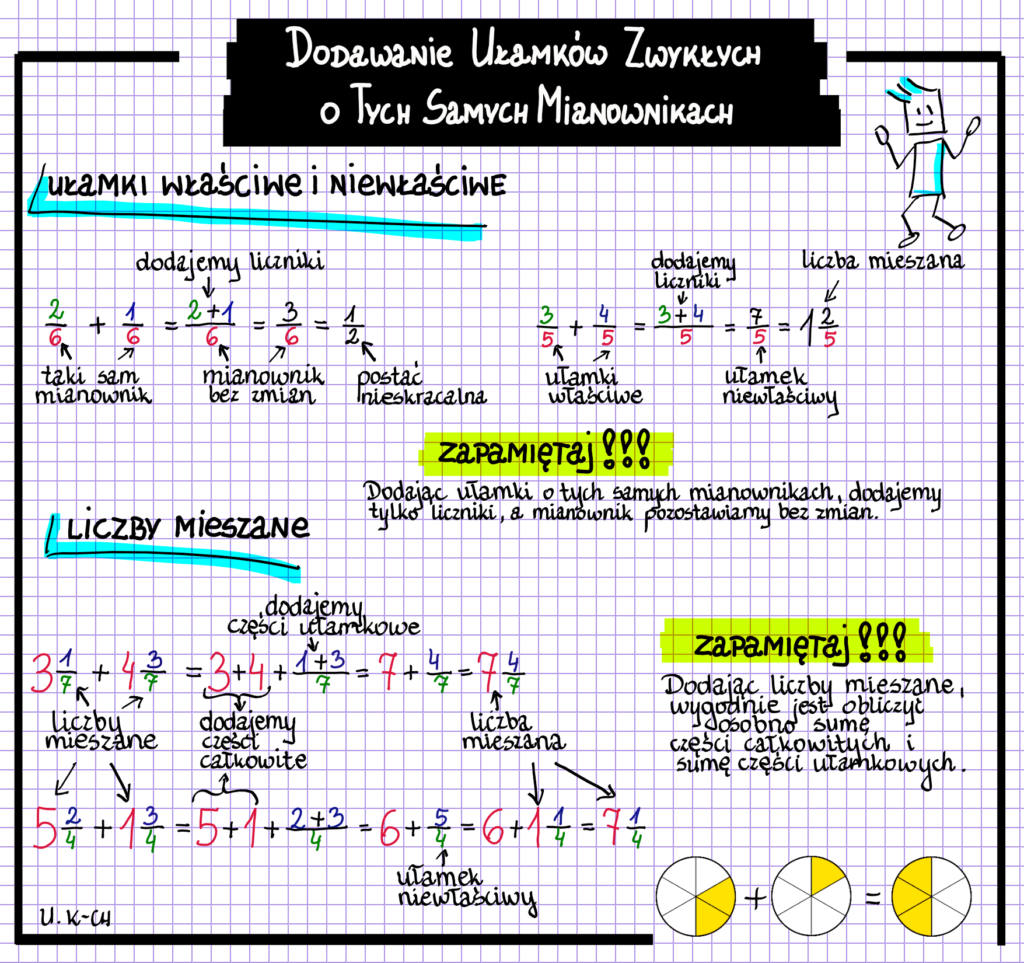
Ułamki właściwe: Ułamki, w których licznik jest mniejszy od mianownika (np. 2/5).
Ułamki niewłaściwe: Ułamki, w których licznik jest większy lub równy mianownikowi (np. 7/3).
Liczby mieszane: Liczby składające się z części całkowitej i ułamka właściwego (np. 2 1/3).

Jeśli mamy do czynienia z liczbami mieszanymi, przed dodawaniem lub odejmowaniem, najczęściej przekształcamy je na ułamki niewłaściwe. Aby to zrobić, mnożymy część całkowitą przez mianownik i dodajemy do licznika. Mianownik pozostaje bez zmian. Na przykład:

2 1/3 = ((2 x 3) + 1) / 3 = 7/3

Następnie postępujemy tak, jak opisałem wcześniej: znajdujemy wspólny mianownik, przekształcamy ułamki i wykonujemy działanie.

Po wykonaniu dodawania lub odejmowania, często konieczne jest uproszczenie ułamka, czyli doprowadzenie go do postaci nieskracalnej. Aby to zrobić, szukamy największego wspólnego dzielnika (NWD) licznika i mianownika i dzielimy przez niego obie liczby. Na przykład, jeśli mamy ułamek 6/8, NWD(6, 8) = 2. Dzielimy licznik i mianownik przez 2:

6/8 = (6 / 2) / (8 / 2) = 3/4

Ułamek 3/4 jest już nieskracalny.

Przykłady na Kartach Pracy

Typowe zadania na kartach pracy mogą wyglądać następująco:

Oblicz: 1/3 + 1/4
Oblicz: 5/6 - 1/2
Oblicz: 2 1/2 + 1 1/4
Oblicz: 3 2/5 - 1 1/10
Uprość wynik: ... (po wykonaniu działania)

Rozwiązując zadania krok po kroku, pamiętajmy o:

Znalezieniu NWW mianowników.
Przekształceniu ułamków do wspólnego mianownika.
Wykonaniu dodawania lub odejmowania liczników.
Uproszczeniu wyniku, jeśli to możliwe.
Zamianie liczb mieszanych na ułamki niewłaściwe przed rozpoczęciem działań.
Zamianie ułamków niewłaściwych na liczby mieszane, jeśli wymaga tego treść zadania.

Uważne śledzenie tych kroków i regularne ćwiczenia zapewnią sukces w rozwiązywaniu zadań z dodawania i odejmowania ułamków o różnych mianownikach. Karty pracy są doskonałym narzędziem do utrwalania tych umiejętności. Pamiętaj, że kluczem jest zrozumienie, dlaczego sprowadzamy ułamki do wspólnego mianownika – aby móc operować na równych częściach całości. Bez tego, dodawanie lub odejmowanie nie ma matematycznego sensu. Dlatego zawsze zaczynaj od upewnienia się, że rozumiesz koncepcję wspólnego mianownika. Wtedy rozwiązywanie zadań stanie się znacznie łatwiejsze i bardziej intuicyjne. Koncentracja i dokładność są niezbędne, aby uniknąć błędów rachunkowych, które mogą prowadzić do niepoprawnych wyników. Po każdym rozwiązaniu zadania warto sprawdzić, czy wynik jest logiczny i czy ułamek został doprowadzony do najprostszej postaci. Ćwiczenie czyni mistrza, więc im więcej zadań rozwiążesz, tym lepiej opanujesz tę umiejętność. A w razie wątpliwości, zawsze pytaj!