Dodawanie I Odejmowanie Ułamków O Jednakowych Mianownikach Zadania

Dodawanie i odejmowanie ułamków o jednakowych mianownikach to jedna z podstawowych operacji w arytmetyce ułamkowej. Zrozumienie i opanowanie tej umiejętności jest kluczowe dla dalszego rozwoju w matematyce. Przejdźmy więc od razu do praktycznych przykładów i zadań.

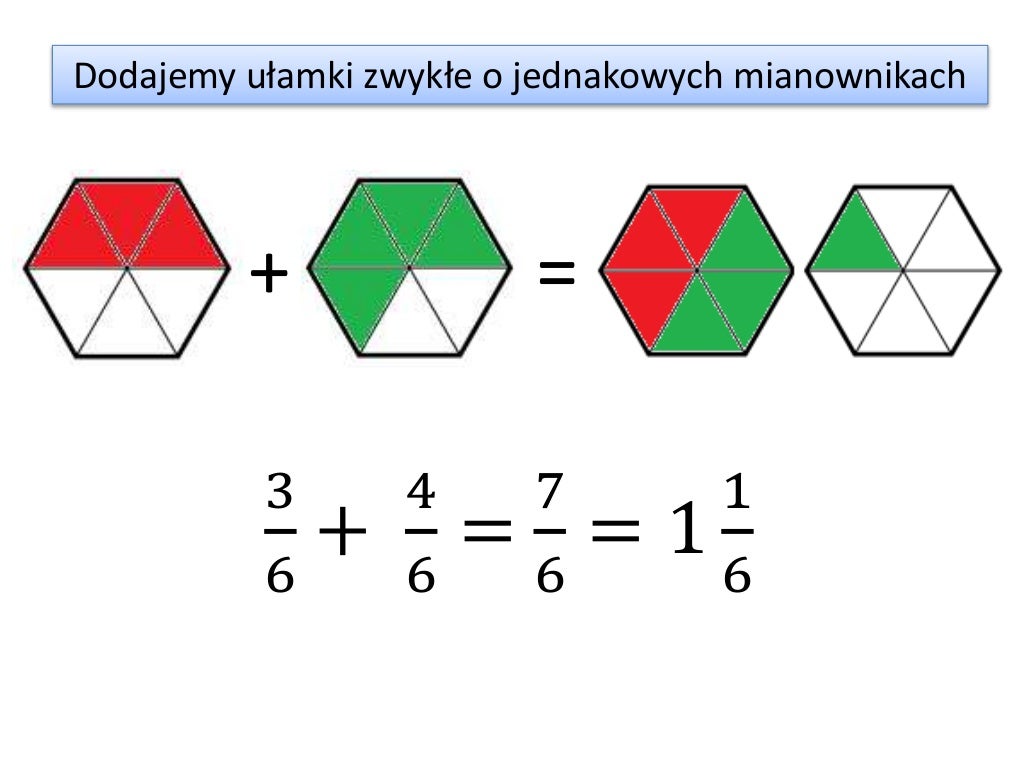
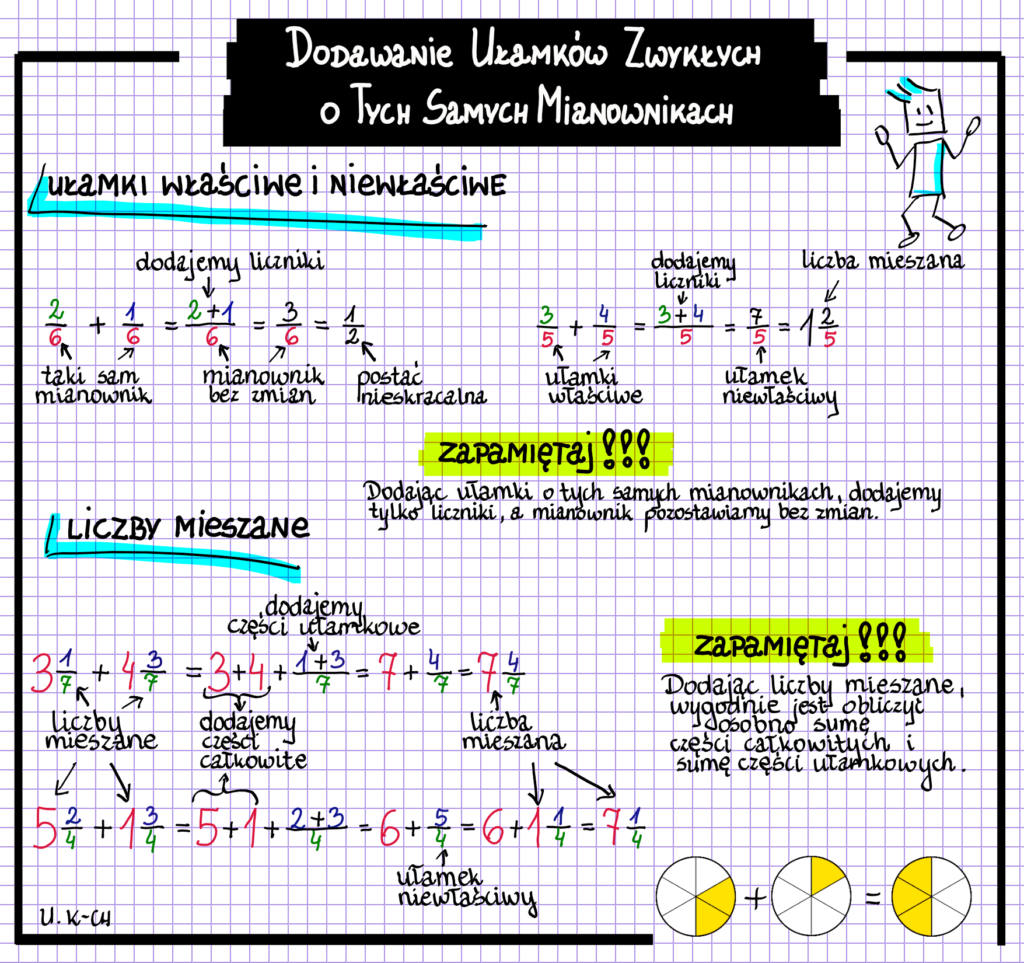
Zacznijmy od dodawania. Jeśli mamy dwa ułamki z tym samym mianownikiem, na przykład 2/5 i 1/5, dodajemy liczniki, a mianownik pozostaje bez zmian. W tym przypadku 2 + 1 = 3, więc 2/5 + 1/5 = 3/5. Kolejny przykład: 3/7 + 2/7. Dodajemy liczniki: 3 + 2 = 5. Zatem wynik to 5/7.

Spróbujmy trudniejszy przykład: 5/12 + 4/12 + 1/12. Sumujemy wszystkie liczniki: 5 + 4 + 1 = 10. Mianownik pozostaje bez zmian, więc wynik to 10/12. Pamiętajmy, że wynik można uprościć, jeśli to możliwe. W tym przypadku 10/12 można uprościć, dzieląc licznik i mianownik przez 2, co daje nam 5/6.

Kolejny przykład: 7/15 + 3/15 + 2/15. Dodajemy liczniki: 7 + 3 + 2 = 12. Wynik to 12/15. Uprawiamy ułamek dzieląc licznik i mianownik przez 3. Otrzymujemy 4/5.

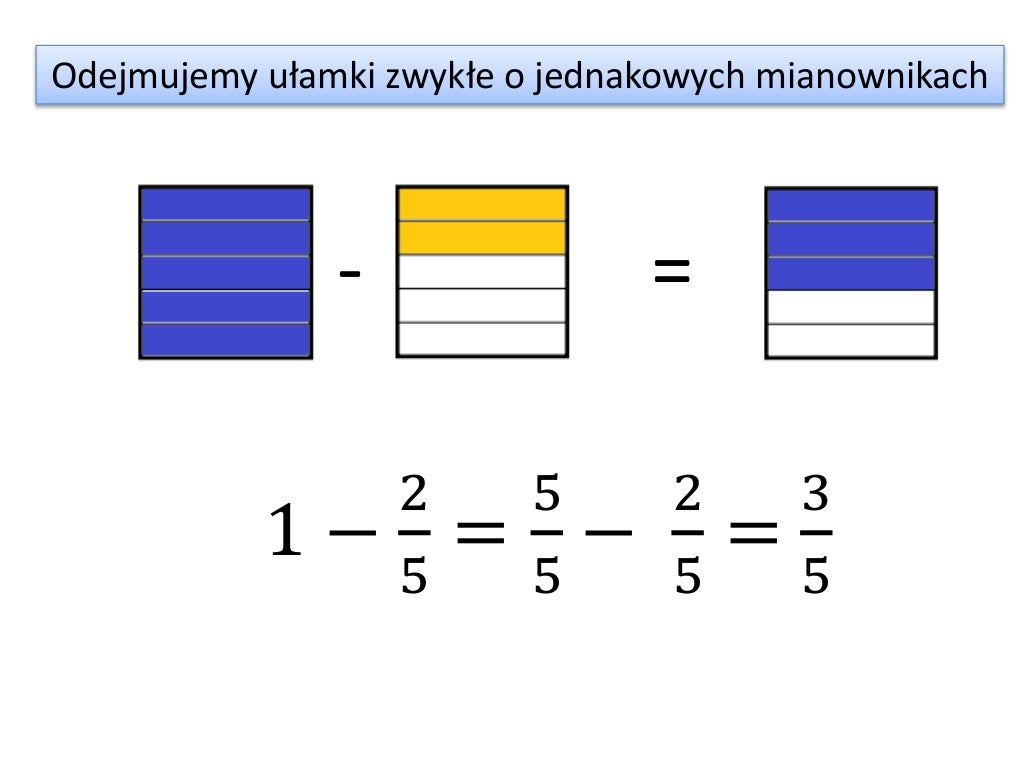
Przejdźmy teraz do odejmowania ułamków o jednakowych mianownikach. Zasada jest bardzo podobna jak przy dodawaniu, ale zamiast dodawać, odejmujemy liczniki. Na przykład, jeśli mamy 4/5 - 1/5, odejmujemy liczniki: 4 - 1 = 3. Mianownik pozostaje bez zmian, więc 4/5 - 1/5 = 3/5.

Następny przykład: 7/9 - 2/9. Odejmujemy liczniki: 7 - 2 = 5. Mianownik bez zmian, więc wynik to 5/9.

Zauważmy, że czasami wynik odejmowania może być zerem. Na przykład, 3/8 - 3/8 = 0/8, co jest po prostu równe 0.

Możemy również wykonywać bardziej złożone operacje, łącząc dodawanie i odejmowanie. Na przykład: 5/11 + 3/11 - 2/11. Najpierw dodajemy 5/11 + 3/11 = 8/11. Następnie odejmujemy 2/11: 8/11 - 2/11 = 6/11.

Inny przykład: 9/13 - 4/13 + 1/13. Najpierw odejmujemy: 9/13 - 4/13 = 5/13. Następnie dodajemy: 5/13 + 1/13 = 6/13.

Zadania praktyczne

Teraz czas na serię zadań, które pozwolą Ci utrwalić zdobytą wiedzę. Pamiętaj, aby zawsze upraszczać wynik, jeśli to możliwe.

1/4 + 2/4 = ?
5/8 + 2/8 = ?
7/10 - 3/10 = ?
9/11 - 5/11 = ?
2/6 + 3/6 = ?
6/7 - 1/7 = ?
3/5 + 1/5 = ?
8/9 - 4/9 = ?
1/3 + 1/3 = ?
10/12 - 6/12 = ?
4/15 + 7/15 = ?
11/14 - 3/14 = ?
2/9 + 5/9 + 1/9 = ?
8/10 - 2/10 - 1/10 = ?
3/7 + 2/7 - 1/7 = ?
6/13 - 2/13 + 5/13 = ?
1/8 + 3/8 + 2/8 = ?
9/11 - 3/11 - 4/11 = ?
4/6 + 1/6 - 2/6 = ?
7/15 - 1/15 + 3/15 = ?

Sprawdź swoje odpowiedzi:

3/4
7/8
4/10 = 2/5
4/11
5/6
5/7
4/5
4/9
2/3
4/12 = 1/3
11/15
8/14 = 4/7
8/9
5/10 = 1/2
4/7
9/13
6/8 = 3/4
2/11
3/6 = 1/2
9/15 = 3/5

Zadania tekstowe

Ułamki często pojawiają się w zadaniach tekstowych. Spróbujmy rozwiązać kilka z nich:

Piotrek zjadł 2/7 pizzy, a Kasia zjadła 3/7 pizzy. Ile pizzy zjedli razem?
Mama upiekła ciasto i pokroiła je na 10 kawałków. Ania zjadła 3/10 ciasta, a Tomek 2/10. Ile ciasta zostało?
W klasie jest 25 uczniów. 2/5 uczniów lubi matematykę, a 1/5 lubi fizykę. Jaka część uczniów lubi matematykę lub fizykę?
Janek miał 8/12 czekolady. Dał Kasi 3/12. Ile czekolady zostało Jankowi?
Basia przeczytała 5/9 książki, a Zosia 2/9. O ile więcej książki przeczytała Basia?
W słoiku było 7/15 dżemu. Mama dołożyła jeszcze 4/15. Ile dżemu jest teraz w słoiku?
Na urodzinach Ewy było 12 dzieci. 1/3 dzieci lubi lody truskawkowe, a 1/4 lody czekoladowe. Jaka część dzieci lubi lody truskawkowe lub czekoladowe? (Uwaga: to zadanie jest trochę trudniejsze, bo wymaga policzenia ile to jest 1/3 z 12 i 1/4 z 12, a następnie dodania tych wyników i podzielenia przez 12 by otrzymać ułamek).
Tata pomalował 3/10 płotu jednego dnia i 4/10 płotu drugiego dnia. Jaką część płotu pomalował tata w ciągu dwóch dni?
W skrzynce z jabłkami 5/14 jabłek to jabłka czerwone, a 6/14 to jabłka zielone. Jaka część jabłek to jabłka czerwone lub zielone?
Magda miała 9/16 sznurka. Użyła 4/16 sznurka do zawiązania paczki. Ile sznurka jej zostało?

Odpowiedzi do zadań tekstowych:

2/7 + 3/7 = 5/7 pizzy
3/10 + 2/10 = 5/10, 10/10 - 5/10 = 5/10 = 1/2 ciasta
2/5 + 1/5 = 3/5 uczniów
8/12 - 3/12 = 5/12 czekolady
5/9 - 2/9 = 3/9 = 1/3 książki
7/15 + 4/15 = 11/15 dżemu
1/3 z 12 = 4, 1/4 z 12 = 3, 4 + 3 = 7, 7/12 dzieci
3/10 + 4/10 = 7/10 płotu
5/14 + 6/14 = 11/14 jabłek
9/16 - 4/16 = 5/16 sznurka

Pamiętaj, że kluczem do sukcesu w matematyce jest praktyka. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zasady i będziesz w stanie radzić sobie z coraz bardziej skomplikowanymi problemami.