Dodawanie I Odejmowanie Ułamków O Jednakowych Mianownikach Oblicz

Dodawanie i odejmowanie ułamków o jednakowych mianownikach to jedna z podstawowych umiejętności w matematyce, która otwiera drzwi do bardziej zaawansowanych operacji na liczbach ułamkowych. Zrozumienie tej koncepcji jest kluczowe dla dalszej nauki matematyki, fizyki, a nawet w życiu codziennym, np. podczas gotowania, mierzenia czy dzielenia. Skupimy się na praktycznym zastosowaniu tej wiedzy, pokazując krok po kroku, jak wykonywać te działania.

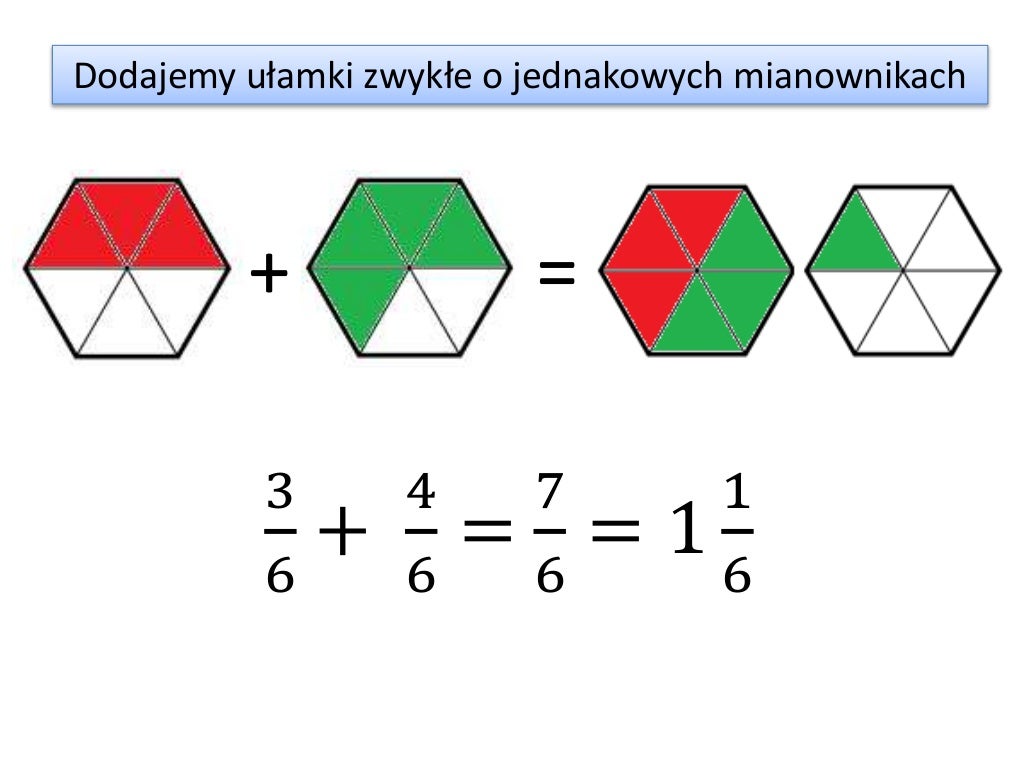
Mając dwa ułamki o jednakowych mianownikach, powiedzmy a/c i b/c, dodawanie sprowadza się do dodania liczników, a mianownik pozostaje bez zmian. Wynik to (a+b)/c.

Przykład: 2/7 + 3/7. Dodajemy liczniki: 2 + 3 = 5. Mianownik pozostaje bez zmian: 7. Wynik to 5/7.

Inny przykład: 1/5 + 2/5 + 1/5. Dodajemy liczniki: 1 + 2 + 1 = 4. Mianownik bez zmian: 5. Wynik: 4/5.

Spójrzmy na bardziej złożony przykład: 4/11 + 5/11 + 1/11. Liczniki: 4 + 5 + 1 = 10. Mianownik: 11. Wynik: 10/11.

A co z liczbami mieszanymi? Można je zamienić na ułamki niewłaściwe. Na przykład, 1 1/3 + 2 1/3. Zamieniamy: 1 1/3 = (13 + 1)/3 = 4/3. 2 1/3 = (23 + 1)/3 = 7/3. Teraz dodajemy: 4/3 + 7/3 = (4+7)/3 = 11/3. Możemy zamienić z powrotem na liczbę mieszaną: 11/3 = 3 2/3.

Kolejny przykład: 2 3/8 + 1 2/8. Zamieniamy: 2 3/8 = (28 + 3)/8 = 19/8. 1 2/8 = (18 + 2)/8 = 10/8. Dodajemy: 19/8 + 10/8 = (19+10)/8 = 29/8. Zamieniamy na liczbę mieszaną: 29/8 = 3 5/8.

Spójrzmy na przypadek, gdy suma liczników jest większa od mianownika, ale można uprościć ułamek. Na przykład: 5/6 + 4/6. Dodajemy: 5 + 4 = 9. Mianownik: 6. Wynik: 9/6. Możemy uprościć, dzieląc licznik i mianownik przez 3: 9/6 = 3/2. A następnie zamienić na liczbę mieszaną: 3/2 = 1 1/2.

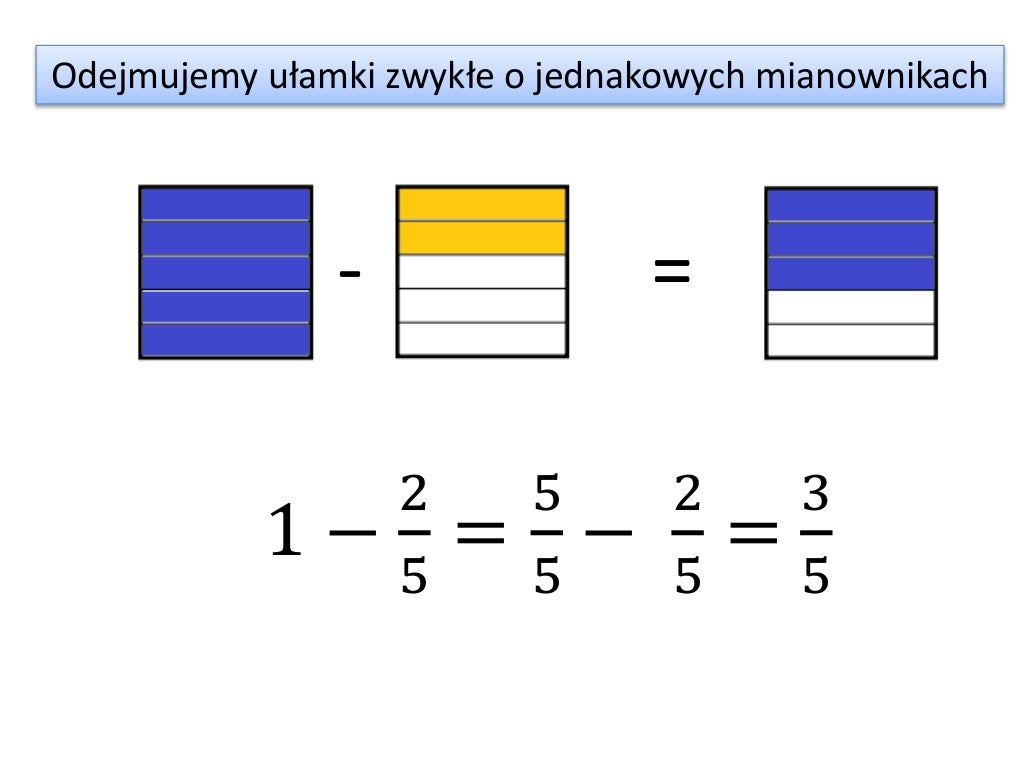
Odejmowanie ułamków o jednakowych mianownikach działa analogicznie. Mając ułamki a/c i b/c, odejmujemy liczniki, zachowując mianownik. Wynik to (a-b)/c.

Przykład: 5/8 - 2/8. Odejmujemy liczniki: 5 - 2 = 3. Mianownik bez zmian: 8. Wynik: 3/8.

Inny przykład: 7/9 - 3/9. Odejmujemy liczniki: 7 - 3 = 4. Mianownik: 9. Wynik: 4/9.

Co zrobić, gdy odejmujemy od liczby mieszanej ułamek? Na przykład, 2 1/4 - 1/4. Zamieniamy liczbę mieszaną na ułamek niewłaściwy: 2 1/4 = (2*4 + 1)/4 = 9/4. Odejmujemy: 9/4 - 1/4 = (9-1)/4 = 8/4. Upraszczamy: 8/4 = 2.

A co, gdy od liczby mieszanej odejmujemy inną liczbę mieszaną? Na przykład, 3 2/5 - 1 1/5. Zamieniamy: 3 2/5 = (35 + 2)/5 = 17/5. 1 1/5 = (15 + 1)/5 = 6/5. Odejmujemy: 17/5 - 6/5 = (17-6)/5 = 11/5. Zamieniamy na liczbę mieszaną: 11/5 = 2 1/5.

Co się stanie, jeśli odejmowany ułamek ma większy licznik niż ułamek, od którego odejmujemy? Na przykład: 1/3 - 2/3. Wynik to (1-2)/3 = -1/3. Wynik jest ujemny.

Rozważmy bardziej skomplikowany przykład odejmowania: 5 3/7 - 2 5/7. Zamieniamy: 5 3/7 = (57 + 3)/7 = 38/7. 2 5/7 = (27 + 5)/7 = 19/7. Odejmujemy: 38/7 - 19/7 = (38-19)/7 = 19/7. Zamieniamy na liczbę mieszaną: 19/7 = 2 5/7.

Przykłady Zastosowania w Praktyce

Wyobraźmy sobie, że pieczemy ciasto. Przepis wymaga 1/4 szklanki cukru, a my chcemy upiec podwójną porcję. Musimy dodać 1/4 + 1/4 szklanki cukru, co daje 2/4 szklanki, czyli 1/2 szklanki.

Inny przykład: mamy 3/5 pizzy i zjadamy 1/5. Ile pizzy nam zostało? Odejmujemy: 3/5 - 1/5 = 2/5. Zostało nam 2/5 pizzy.

Wyobraźmy sobie, że biegamy. Przebiegliśmy 2/7 trasy i chcemy przebiec jeszcze 3/7 trasy. Ile trasy łącznie przebiegniemy? Dodajemy: 2/7 + 3/7 = 5/7. Przebiegniemy 5/7 trasy.

Trudniejsze przypadki

Czasami, zanim wykonamy dodawanie lub odejmowanie, trzeba uprościć ułamki, aby miały taki sam mianownik (chociaż w tym przypadku, mianowniki są już takie same). Rozważmy przykład: 6/8 + 1/8. Dodajemy: 6/8 + 1/8 = 7/8. Ułamek 7/8 jest już w postaci uproszczonej.

A co, jeśli mamy do czynienia z więcej niż dwoma ułamkami? Na przykład: 1/10 + 3/10 + 2/10. Dodajemy liczniki: 1 + 3 + 2 = 6. Mianownik: 10. Wynik: 6/10. Upraszczamy, dzieląc licznik i mianownik przez 2: 6/10 = 3/5.

Inny przykład z odejmowaniem: 9/12 - 2/12 - 1/12. Odejmujemy liczniki: 9 - 2 - 1 = 6. Mianownik: 12. Wynik: 6/12. Upraszczamy, dzieląc licznik i mianownik przez 6: 6/12 = 1/2.

Podsumowując, dodawanie i odejmowanie ułamków o jednakowych mianownikach jest proste, gdy pamiętamy o podstawowej zasadzie: operujemy na licznikach, a mianownik pozostaje bez zmian. Kluczem jest praktyka i zrozumienie, jak te operacje przekładają się na rzeczywiste sytuacje. Pamiętajmy o upraszczaniu wyników, gdy jest to możliwe, aby uzyskać najprostszą formę ułamka.