Dodawanie I Odejmowanie Ułamków O Jednakowych Mianownikach Karta Pracy

Czy Twoje dziecko ma trudności z dodawaniem i odejmowaniem ułamków o jednakowych mianownikach? Nie martw się, to częsty problem! Ta karta pracy ma na celu pomóc uczniom klas 4-6 zrozumieć i opanować te podstawowe operacje matematyczne. Przygotuj się na ekscytującą podróż po świecie ułamków!

Wprowadzenie do Ułamków

Zanim przejdziemy do dodawania i odejmowania, upewnijmy się, że rozumiemy, czym są ułamki. Wyobraź sobie pizzę podzieloną na równe kawałki. Każdy z tych kawałków to ułamek całej pizzy.

Ułamek składa się z dwóch części:

• Licznik: Pokazuje, ile kawałków pizzy mamy (górna liczba).
• Mianownik: Pokazuje, na ile kawałków została podzielona cała pizza (dolna liczba).

Na przykład, ułamek ³/₈ oznacza, że mamy 3 kawałki pizzy podzielonej na 8 równych części.

Dlaczego Ułamki Są Ważne?

Ułamki są wszędzie! Używamy ich podczas gotowania (np. ½ szklanki mąki), mierzenia (np. ¼ metra materiału), a nawet podczas dzielenia się pizzą ze znajomymi. Zrozumienie ułamków jest kluczowe dla wielu aspektów życia.

Dodawanie Ułamków o Jednakowych Mianownikach

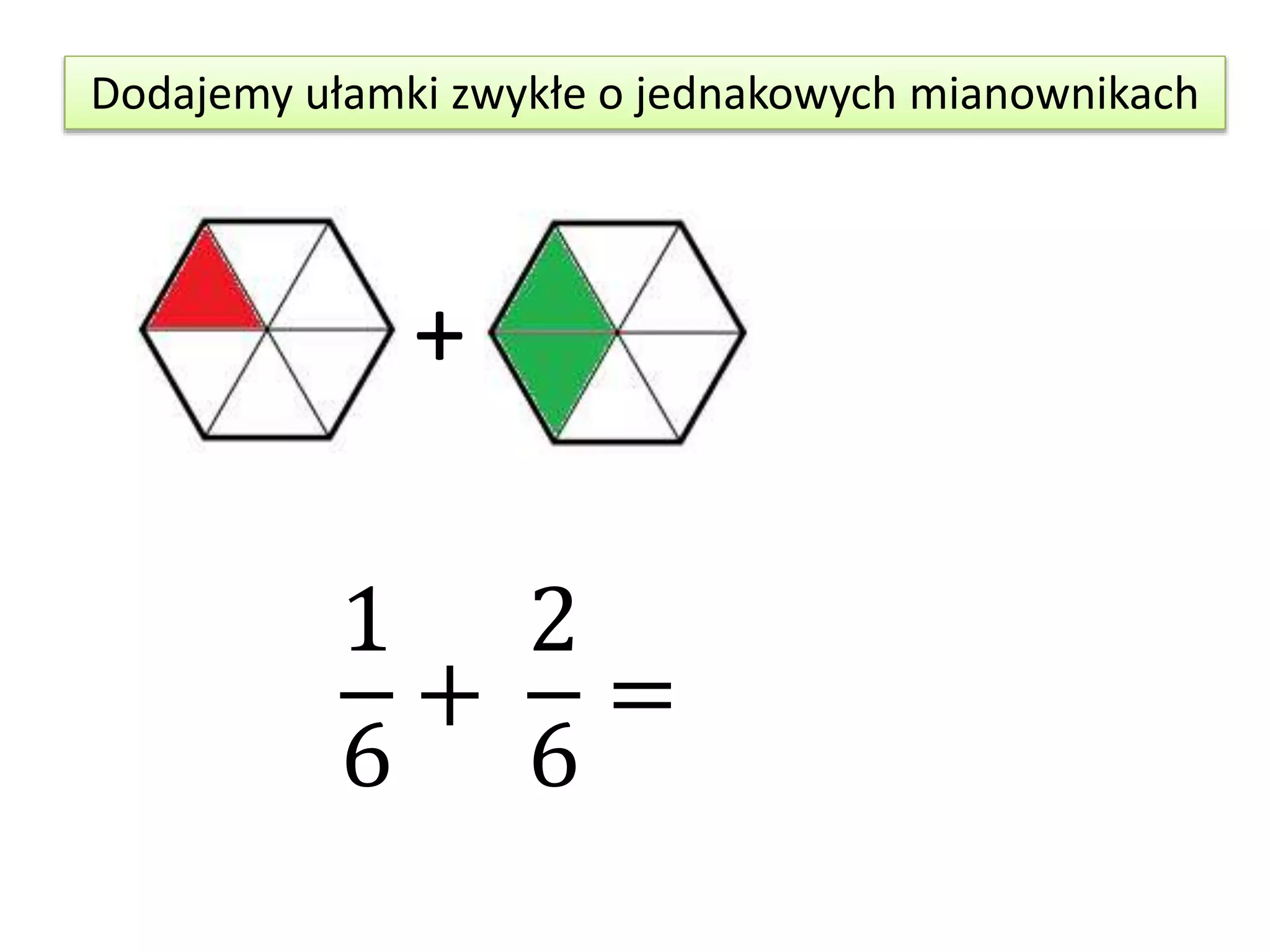
Dodawanie ułamków o jednakowych mianownikach jest prostsze, niż się wydaje. Kiedy mianowniki są takie same, możemy po prostu dodać liczniki, a mianownik pozostawić bez zmian.

Zasada: Jeśli mamy ułamki ^a/_c i ^b/_c, to ich suma wynosi ^{(a + b)}/_c.

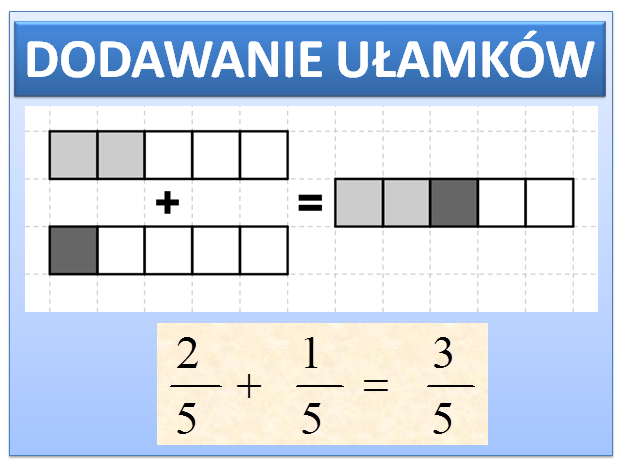
Przykład: ¹/₅ + ²/₅ = ^{(1 + 2)}/₅ = ³/₅.

Wyjaśnienie: Wyobraź sobie, że masz jedną piątą pizzy i dodajesz do niej dwie piąte pizzy. Razem masz trzy piąte pizzy.

Krok po Kroku: Jak Dodawać Ułamki

1. Sprawdź mianowniki: Upewnij się, że mianowniki są takie same. Jeśli nie są, musimy je najpierw doprowadzić do wspólnego mianownika (o tym później!).
2. Dodaj liczniki: Dodaj liczby znajdujące się w licznikach.
3. Przepisz mianownik: Mianownik pozostaje taki sam.
4. Uprość ułamek (jeśli to możliwe): Jeśli licznik i mianownik mają wspólny dzielnik, możemy uprościć ułamek. Na przykład, ułamek ⁴/₈ można uprościć do ¹/₂.

Przykłady Dodatkowe:

• ³/₇ + ²/₇ = ⁵/₇
• ⁴/₉ + ¹/₉ = ⁵/₉
• ⁵/₁₂ + ³/₁₂ = ⁸/₁₂ (można uprościć do ²/₃)

Odejmowanie Ułamków o Jednakowych Mianownikach

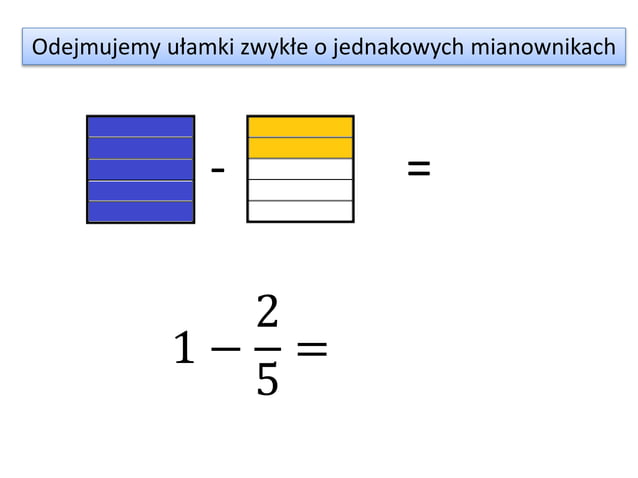
Odejmowanie ułamków o jednakowych mianownikach jest bardzo podobne do dodawania. Zamiast dodawać liczniki, odejmujemy je.

Zasada: Jeśli mamy ułamki ^a/_c i ^b/_c, to ich różnica wynosi ^{(a - b)}/_c.

Przykład: ⁴/₅ - ¹/₅ = ^{(4 - 1)}/₅ = ³/₅.

Wyjaśnienie: Wyobraź sobie, że masz cztery piąte pizzy i zjadasz jedną piątą. Zostają ci trzy piąte pizzy.

Krok po Kroku: Jak Odejmować Ułamki

1. Sprawdź mianowniki: Upewnij się, że mianowniki są takie same.
2. Odejmij liczniki: Odejmij liczbę znajdującą się w drugim liczniku od liczby znajdującej się w pierwszym liczniku.
3. Przepisz mianownik: Mianownik pozostaje taki sam.
4. Uprość ułamek (jeśli to możliwe): Uprość ułamek, jeśli to możliwe.

Przykłady Dodatkowe:

• ⁶/₈ - ²/₈ = ⁴/₈ (można uprościć do ¹/₂)
• ⁷/₁₀ - ³/₁₀ = ⁴/₁₀ (można uprościć do ²/₅)
• ⁹/₁₁ - ⁴/₁₁ = ⁵/₁₁

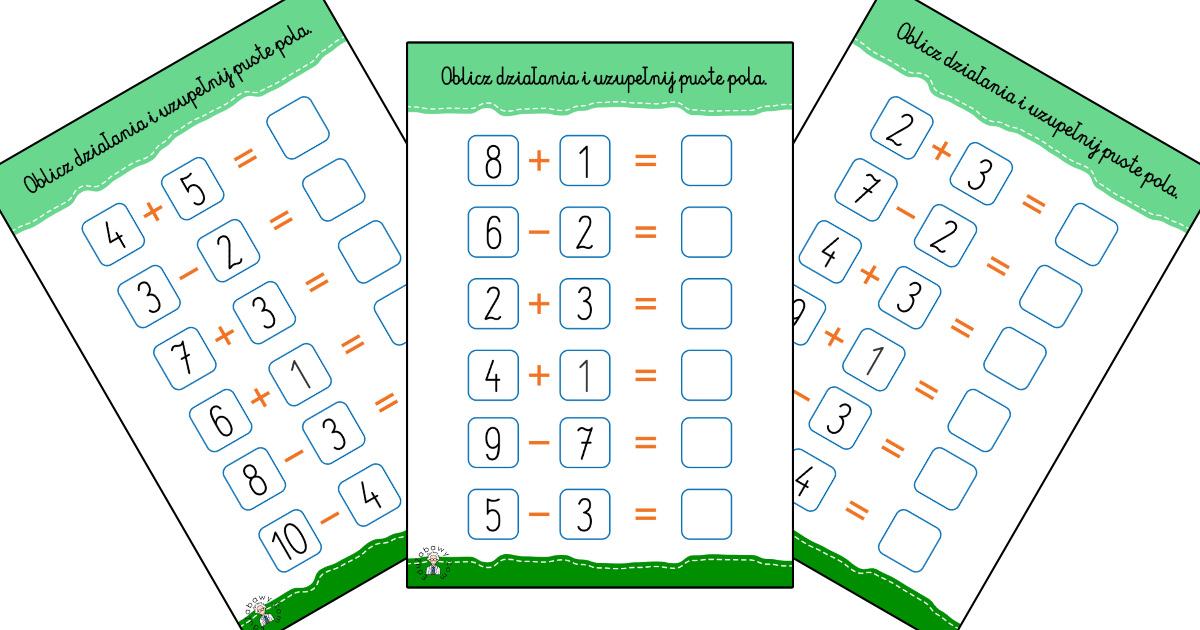
Karta Pracy: Ćwiczenia Praktyczne

Teraz, kiedy znasz zasady, czas na praktykę! Poniżej znajdziesz kilka ćwiczeń, które pomogą Ci utrwalić zdobytą wiedzę.

Zadanie 1: Dodawanie Ułamków

1. ²/₆ + ³/₆ = ?
2. ¹/₄ + ²/₄ = ?
3. ⁴/₁₀ + ⁵/₁₀ = ?
4. ³/₈ + ⁴/₈ = ?
5. ²/₉ + ⁵/₉ = ?

Zadanie 2: Odejmowanie Ułamków

1. ⁵/₇ - ²/₇ = ?
2. ³/₅ - ¹/₅ = ?
3. ⁸/₁₂ - ³/₁₂ = ?
4. ⁶/₉ - ²/₉ = ?
5. ⁷/₁₁ - ⁴/₁₁ = ?

Zadanie 3: Dodawanie i Odejmowanie Ułamków - Mieszane

1. ³/₁₀ + ⁴/₁₀ - ²/₁₀ = ?
2. ⁶/₈ - ¹/₈ + ²/₈ = ?
3. ²/₅ + ²/₅ - ¹/₅ = ?

Pamiętaj: Po rozwiązaniu każdego zadania, sprawdź, czy możesz uprościć ułamek!

Wskazówki i Triki

• Wyobraź sobie obrazowo: Używaj obrazków, takich jak pizza lub koło, aby wizualizować ułamki. To pomoże Ci lepiej zrozumieć, co robisz.
• Uprość ułamki: Zawsze sprawdzaj, czy możesz uprościć wynikowy ułamek. To sprawi, że Twoje odpowiedzi będą bardziej eleganckie i łatwiejsze do zrozumienia.
• Praktyka czyni mistrza: Im więcej ćwiczysz, tym lepiej będziesz radzić sobie z ułamkami. Nie zrażaj się, jeśli na początku jest trudno.
• Sprawdzaj swoje odpowiedzi: Upewnij się, że Twoje odpowiedzi są poprawne. Możesz użyć kalkulatora lub poprosić kogoś o sprawdzenie.

Rozwiązywanie Problemów z Życia Codziennego

Spróbujmy zastosować naszą wiedzę o ułamkach do rozwiązywania problemów z życia codziennego.

Przykład 1: Ania zjadła ²/₇ ciasta, a Janek zjadł ³/₇ ciasta. Ile ciasta zjedli razem?

Rozwiązanie: ²/₇ + ³/₇ = ⁵/₇. Razem zjedli ⁵/₇ ciasta.

Przykład 2: Marcin miał ⁵/₆ soku. Wypiła ²/₆ soku. Ile soku mu zostało?

Rozwiązanie: ⁵/₆ - ²/₆ = ³/₆. Marcinowi zostało ³/₆ soku (można uprościć do ¹/₂).

Pamiętaj: Zawsze przeczytaj uważnie treść zadania i upewnij się, że rozumiesz, o co pytają.

Co Dalej?

Gratulacje! Opanowałeś dodawanie i odejmowanie ułamków o jednakowych mianownikach! Co możesz zrobić dalej?

• Ułamki o różnych mianownikach: Naucz się dodawać i odejmować ułamki, które mają różne mianowniki. To wymaga znalezienia wspólnego mianownika.
• Mnożenie i dzielenie ułamków: Naucz się mnożyć i dzielić ułamki. To otworzy przed Tobą nowe możliwości.
• Ułamki dziesiętne: Dowiedz się, jak zamieniać ułamki zwykłe na ułamki dziesiętne i odwrotnie.

Pamiętaj, że matematyka to przygoda! Nie bój się eksperymentować, zadawać pytania i uczyć się na błędach. Każdy krok naprzód to powód do dumy. Powodzenia!

Ułamki są podstawą wielu dziedzin matematyki i nauki. Ich opanowanie otwiera drzwi do dalszej edukacji i rozwoju. Dodawanie i odejmowanie to kluczowe umiejętności, które warto doskonalić. Nie poddawaj się i ciesz się procesem nauki!