Dodawanie I Odejmowanie Ułamków O Jednakowych Mianownikach

Dodawanie i odejmowanie ułamków o jednakowych mianownikach to jedna z podstawowych operacji arytmetycznych, którą każdy uczeń powinien opanować. Jest to fundament do dalszego zrozumienia bardziej skomplikowanych działań na ułamkach. Zobaczmy, jak to wygląda w praktyce.

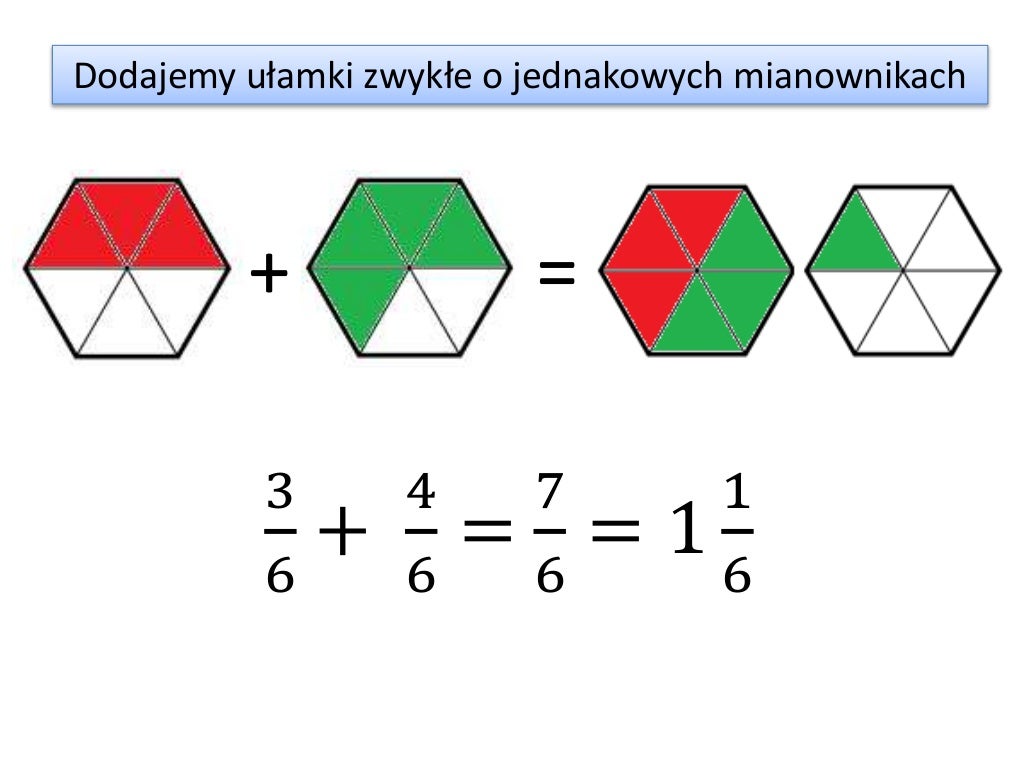
Mamy dwa ułamki: 3/7 oraz 2/7. Oba mają ten sam mianownik, czyli 7. Aby je dodać, sumujemy liczniki, a mianownik pozostaje bez zmian. Zatem 3/7 + 2/7 = (3+2)/7 = 5/7. Proste, prawda?

Spójrzmy na inny przykład. Dodajmy 1/5 oraz 3/5. Ponownie, mianownik jest taki sam (5). Dodajemy liczniki: 1 + 3 = 4. Wynik to 4/5.

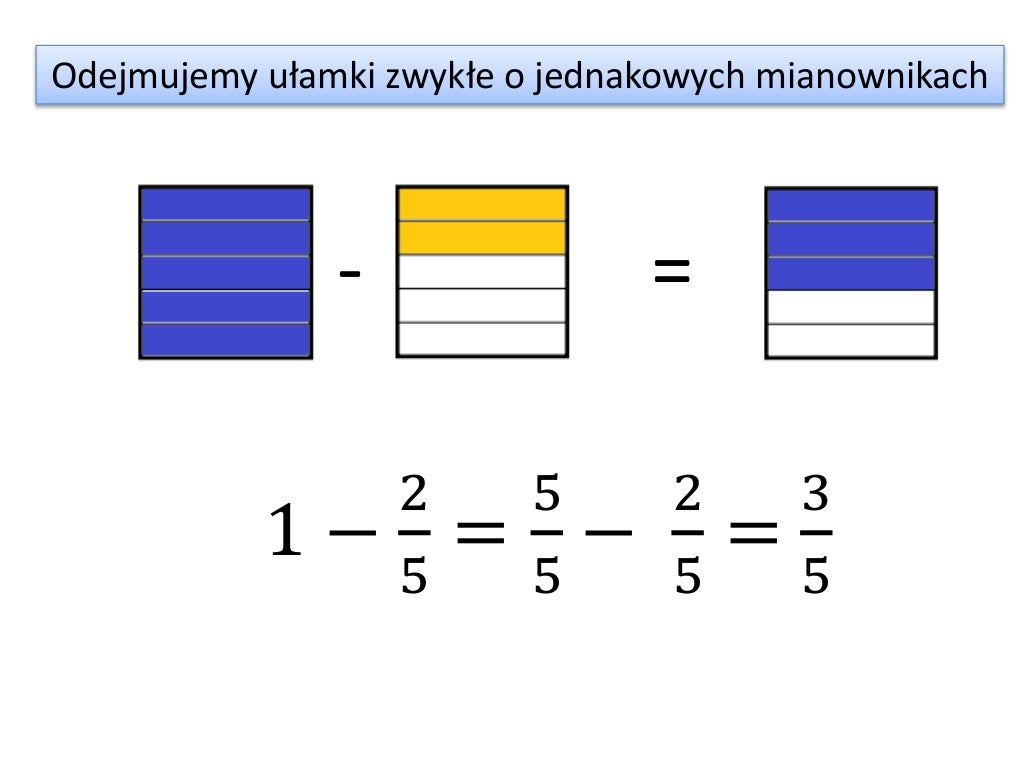
A co z odejmowaniem? Zasada jest bardzo podobna. Mamy dwa ułamki: 5/9 oraz 2/9. Odejmujemy liczniki, a mianownik zostaje bez zmian. 5/9 - 2/9 = (5-2)/9 = 3/9. Warto zauważyć, że w tym przypadku ułamek 3/9 można skrócić, dzieląc licznik i mianownik przez 3. Otrzymujemy wtedy 1/3.

Weźmy inny przykład odejmowania. Mamy 7/10 i 3/10. Odejmujemy: 7/10 - 3/10 = (7-3)/10 = 4/10. Ponownie, możemy skrócić ułamek 4/10, dzieląc licznik i mianownik przez 2. Otrzymujemy 2/5.

Przykłady i zastosowania

Zobaczmy kilka bardziej rozbudowanych przykładów. Załóżmy, że mamy do dodania trzy ułamki: 1/8, 3/8 oraz 2/8. Wszystkie mają ten sam mianownik (8). Dodajemy liczniki: 1 + 3 + 2 = 6. Zatem 1/8 + 3/8 + 2/8 = 6/8. Ułamek 6/8 można skrócić, dzieląc licznik i mianownik przez 2. Otrzymujemy 3/4.

Inny przykład: Dodajmy 5/12, 1/12 oraz 4/12. Wszystkie ułamki mają mianownik 12. Sumujemy liczniki: 5 + 1 + 4 = 10. Więc 5/12 + 1/12 + 4/12 = 10/12. Ułamek 10/12 można skrócić, dzieląc licznik i mianownik przez 2. Otrzymujemy 5/6.

A co z odejmowaniem, gdy mamy więcej niż dwa ułamki? Na przykład: 9/11 - 2/11 - 3/11. Wszystkie mają mianownik 11. Odejmujemy liczniki kolejno: 9 - 2 - 3 = 4. Wynik to 4/11.

Inny przykład: 11/15 - 4/15 - 1/15. Wszystkie mają mianownik 15. Odejmujemy liczniki: 11 - 4 - 1 = 6. Zatem 11/15 - 4/15 - 1/15 = 6/15. Ułamek 6/15 można skrócić, dzieląc licznik i mianownik przez 3. Otrzymujemy 2/5.

Dodawanie i odejmowanie ułamków o jednakowych mianownikach pojawia się w wielu sytuacjach życiowych. Na przykład, jeśli pieczemy ciasto i używamy 1/4 szklanki mąki, a następnie dodamy jeszcze 2/4 szklanki mąki, to łącznie użyliśmy 1/4 + 2/4 = 3/4 szklanki mąki.

Inny przykład: Jeśli mamy 7/10 litra soku, a wypijemy 2/10 litra, to zostanie nam 7/10 - 2/10 = 5/10 litra soku. Możemy skrócić 5/10 do 1/2 litra.

Uważaj na pułapki

Podczas dodawania i odejmowania ułamków o jednakowych mianownikach, ważne jest, aby pamiętać o kilku rzeczach:

Zawsze sprawdzaj, czy mianowniki są takie same. Jeśli nie są, nie możesz bezpośrednio dodawać lub odejmować liczników. Będziesz musiał najpierw sprowadzić ułamki do wspólnego mianownika.
Pamiętaj o skracaniu ułamków. Po wykonaniu działania, zawsze sprawdź, czy wynikowy ułamek można skrócić. Skracanie ułamków upraszcza wynik i często ułatwia dalsze obliczenia.
Uważaj na liczby mieszane. Jeśli masz liczby mieszane, możesz je zamienić na ułamki niewłaściwe przed wykonaniem dodawania lub odejmowania. Na przykład, 1 1/2 to to samo co 3/2.
Zwracaj uwagę na kolejność wykonywania działań. Jeśli masz więcej niż jedno działanie, pamiętaj o kolejności wykonywania działań (najpierw nawiasy, potem mnożenie i dzielenie, a na końcu dodawanie i odejmowanie).

Dodawanie i odejmowanie ułamków o jednakowych mianownikach to fundament do dalszego zrozumienia ułamków. Im lepiej to opanujesz, tym łatwiejsze staną się bardziej skomplikowane działania. Regularna praktyka i rozwiązywanie różnych przykładów pomogą Ci utrwalić wiedzę i uniknąć błędów.

Pamiętaj, że matematyka to nie tylko zbiór reguł, ale także narzędzie do rozwiązywania problemów. Im lepiej rozumiesz zasady, tym łatwiej będziesz mógł zastosować je w praktyce.

Ćwicz regularnie, rozwiązuj zadania i nie bój się pytać, jeśli masz wątpliwości. Powodzenia!

Opanowanie dodawania i odejmowania ułamków o jednakowych mianownikach otwiera drzwi do bardziej zaawansowanych koncepcji matematycznych. To fundament, na którym buduje się zrozumienie ułamków i ich zastosowań. Dlatego warto poświęcić czas na dokładne opanowanie tej umiejętności.

Pamiętaj, że każde zadanie matematyczne to wyzwanie, które można pokonać. Z cierpliwością i systematycznością, każdy może osiągnąć sukces w matematyce.