Dodawanie I Odejmowanie Ułamków Klasa 5

Hej Uczniowie Klasy 5! Gotowi na przygodę z ułamkami? Nie martwcie się, dodawanie i odejmowanie ułamków to nic strasznego! Pomyślcie o tym jak o dzieleniu pizzy – dodajemy kawałki, żeby było jej więcej, a odejmujemy, żeby zostało mniej. Ten artykuł pomoże Wam przygotować się do sprawdzianu, krok po kroku.
Czym są ułamki? Krótka powtórka
Zanim przejdziemy do dodawania i odejmowania, upewnijmy się, że dobrze rozumiemy, czym jest ułamek. Ułamek to część całości. Składa się z dwóch części:
- Licznik (górna część): Mówi nam, ile mamy kawałków.
- Mianownik (dolna część): Mówi nam, na ile części podzielona jest całość.
Na przykład, w ułamku 3/4, 3 to licznik, a 4 to mianownik. Oznacza to, że mamy 3 kawałki z pizzy podzielonej na 4 części.
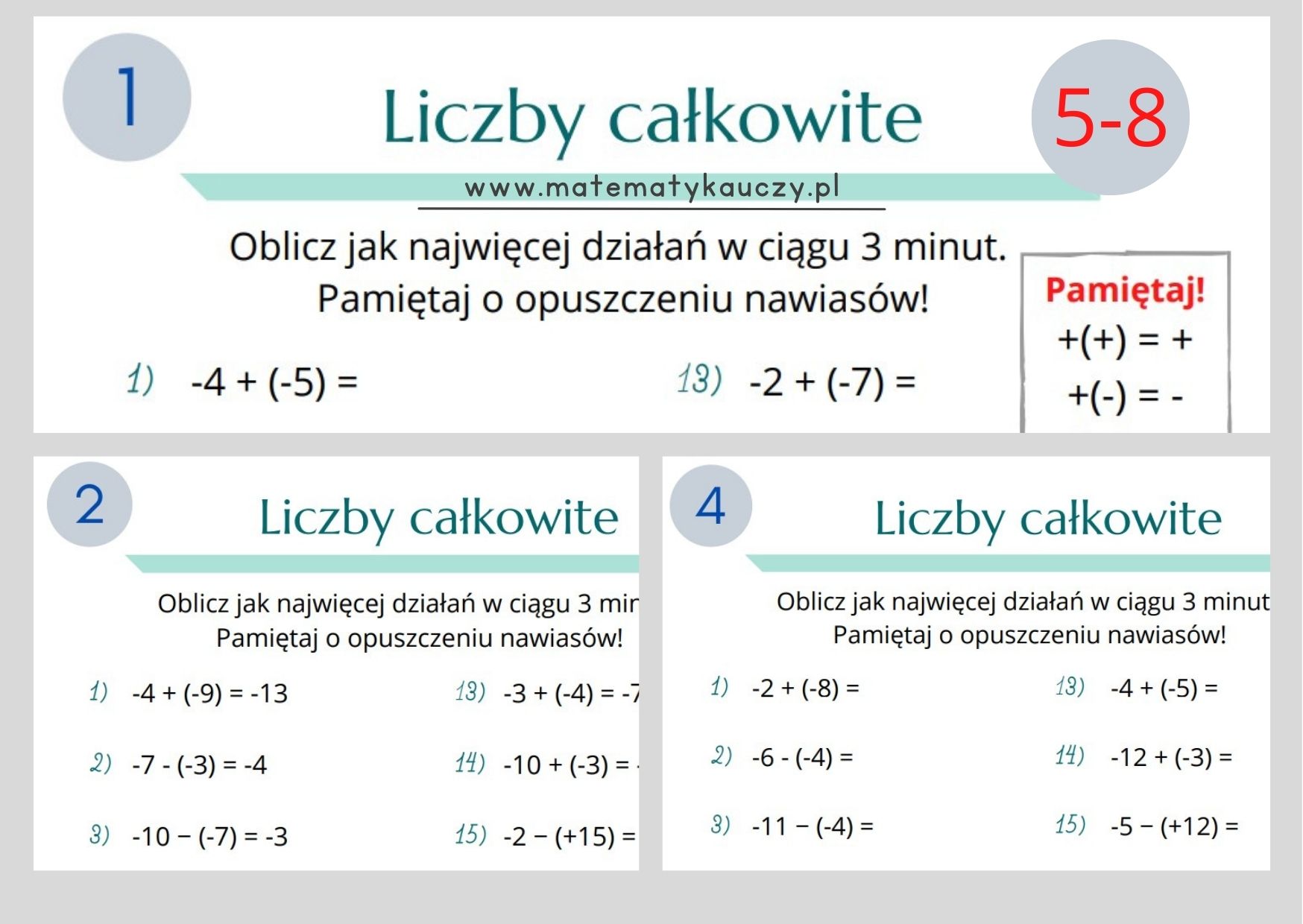
Dodawanie i Odejmowanie Ułamków o Wspólnym Mianowniku
To najłatwiejszy przypadek! Jeśli ułamki, które chcemy dodać lub odjąć, mają ten sam mianownik, po prostu dodajemy lub odejmujemy ich liczniki. Mianownik pozostaje bez zmian.
Przykład Dodawania
Załóżmy, że chcemy dodać 1/5 + 2/5. Ponieważ mianowniki są takie same (5), dodajemy tylko liczniki: 1 + 2 = 3. Więc 1/5 + 2/5 = 3/5.
Przykład Odejmowania
A co, jeśli chcemy odjąć 4/7 - 1/7? Ponownie, mianowniki są takie same (7). Odejmujemy liczniki: 4 - 1 = 3. Więc 4/7 - 1/7 = 3/7.
Pamiętajcie, to naprawdę proste, jeśli mianowniki są takie same! Skupcie się tylko na licznikach.
Dodawanie i Odejmowanie Ułamków o Różnych Mianownikach
Tutaj zaczyna się robić trochę ciekawiej, ale bez obaw! Kluczem jest znalezienie wspólnego mianownika. Najczęściej szukamy najmniejszej wspólnej wielokrotności (NWW) mianowników.
Co to jest Najmniejsza Wspólna Wielokrotność (NWW)?
NWW to najmniejsza liczba, która jest wielokrotnością obu mianowników. Innymi słowy, to najmniejsza liczba, przez którą oba mianowniki się dzielą.
Przykład: Znajdźmy NWW dla liczb 3 i 4. Wielokrotności 3: 3, 6, 9, 12, 15... Wielokrotności 4: 4, 8, 12, 16... Najmniejsza wspólna wielokrotność to 12.
Kroki do Dodawania/Odejmowania Ułamków o Różnych Mianownikach
- Znajdź NWW mianowników. To będzie nasz wspólny mianownik.
- Rozszerz każdy ułamek, tak aby miał wspólny mianownik. Pamiętaj, żeby pomnożyć zarówno licznik, jak i mianownik przez tę samą liczbę!
- Teraz, gdy ułamki mają wspólny mianownik, dodaj lub odejmij ich liczniki.
- Uprość ułamek, jeśli to możliwe.
Przykład Dodawania z Różnymi Mianownikami
Dodajmy 1/3 + 1/4.
- NWW dla 3 i 4 to 12.
- Rozszerzamy 1/3: 1/3 * 4/4 = 4/12
- Rozszerzamy 1/4: 1/4 * 3/3 = 3/12
- Teraz dodajemy: 4/12 + 3/12 = 7/12
Więc 1/3 + 1/4 = 7/12.
Przykład Odejmowania z Różnymi Mianownikami
Odejmijmy 2/5 - 1/10.
- NWW dla 5 i 10 to 10.
- Rozszerzamy 2/5: 2/5 * 2/2 = 4/10
- 1/10 już ma odpowiedni mianownik, więc nic nie zmieniamy.
- Teraz odejmujemy: 4/10 - 1/10 = 3/10
Więc 2/5 - 1/10 = 3/10.
Ułamki Niewłaściwe i Liczby Mieszane
Ułamek niewłaściwy to taki, w którym licznik jest większy lub równy mianownikowi (np. 5/3). Liczba mieszana to liczba składająca się z liczby całkowitej i ułamka (np. 12/3).
Zamiana Ułamka Niewłaściwego na Liczbę Mieszaną
Dzielimy licznik przez mianownik. Wynik dzielenia to liczba całkowita, reszta to nowy licznik, a mianownik pozostaje bez zmian.
Przykład: Zamieńmy 7/3 na liczbę mieszaną. 7 : 3 = 2 (reszty 1). Więc 7/3 = 21/3.
Zamiana Liczby Mieszanej na Ułamek Niewłaściwy
Mnożymy liczbę całkowitą przez mianownik i dodajemy do licznika. Wynik to nowy licznik, a mianownik pozostaje bez zmian.
Przykład: Zamieńmy 12/5 na ułamek niewłaściwy. 1 * 5 + 2 = 7. Więc 12/5 = 7/5.
Dodawanie i Odejmowanie Liczb Mieszanych
Możemy zrobić to na dwa sposoby:
- Zamienić liczby mieszane na ułamki niewłaściwe, dodać/odjąć ułamki, a następnie zamienić wynik z powrotem na liczbę mieszaną.
- Dodać/odjąć oddzielnie liczby całkowite i ułamki. Jeśli po dodaniu/odjęciu ułamków otrzymamy ułamek niewłaściwy, zamieniamy go na liczbę mieszaną i dodajemy liczbę całkowitą do części całkowitej początkowej liczby mieszanej.
Upraszczanie Ułamków
Upraszczanie ułamka polega na znalezieniu największego wspólnego dzielnika (NWD) licznika i mianownika i podzieleniu obu przez ten dzielnik. Dzięki temu ułamek będzie miał najmniejsze możliwe liczby w liczniku i mianowniku.
Przykład: Uprośćmy ułamek 6/8. NWD dla 6 i 8 to 2. Dzielimy 6 przez 2 i 8 przez 2. Otrzymujemy 3/4.
Podsumowanie – Kluczowe Punkty
- Ułamek: Licznik / Mianownik.
- Wspólny Mianownik: Potrzebny do dodawania i odejmowania.
- NWW: Najmniejsza Wspólna Wielokrotność – najlepszy wspólny mianownik.
- Rozszerzanie Ułamka: Mnożymy licznik i mianownik przez tę samą liczbę.
- Upraszczanie Ułamka: Dzielimy licznik i mianownik przez ich NWD.
- Ułamek Niewłaściwy: Licznik ≥ Mianownik.
- Liczba Mieszana: Liczba Całkowita + Ułamek.
Pamiętajcie, praktyka czyni mistrza! Rozwiążcie jak najwięcej zadań, a na sprawdzianie na pewno pójdzie Wam świetnie. Powodzenia!
Trzymam za Was kciuki!