Dodawanie I Odejmowanie Ułamków Dziesiętnych Klasa 6

Ułamki dziesiętne to liczby, które zapisujemy z użyciem przecinka, gdzie cyfry po przecinku oznaczają części dziesiętne, setne, tysięczne i tak dalej. Dodawanie i odejmowanie ułamków dziesiętnych to podstawowe umiejętności matematyczne, które przydadzą się w wielu sytuacjach życiowych, od robienia zakupów po planowanie budżetu. W klasie 6 zagadnienie to jest omawiane szczegółowo, a ten artykuł ma na celu pomóc Ci w zrozumieniu i opanowaniu tej umiejętności.

Zacznijmy od dodawania. Aby dodać dwa lub więcej ułamków dziesiętnych, postępujemy zgodnie z kilkoma prostymi krokami. Najważniejsze jest poprawne ułożenie liczb w słupku.

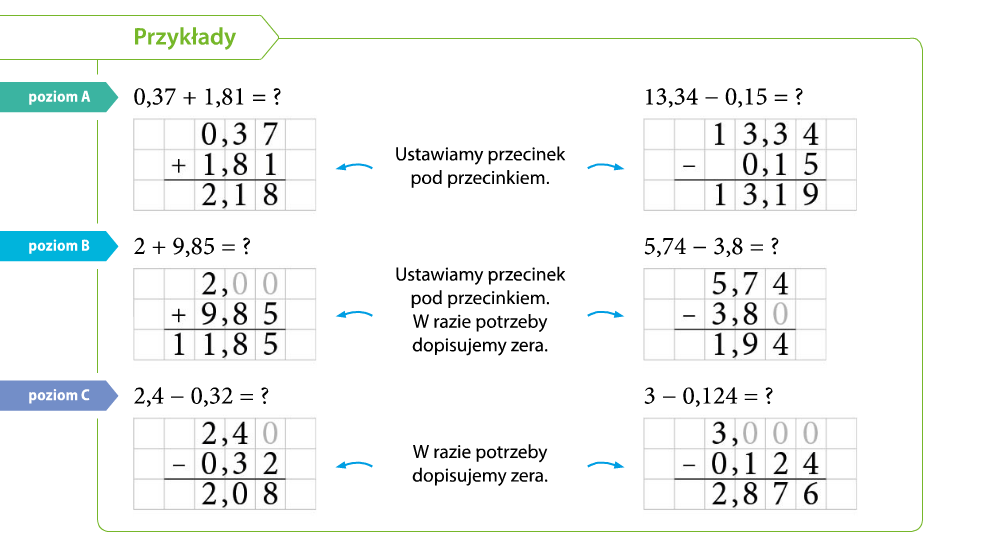
Pierwszy krok to zapisanie ułamków jeden pod drugim, tak aby przecinki znajdowały się w jednej linii pionowej. Jest to kluczowe, ponieważ zapewnia, że dodajemy do siebie odpowiednie wartości – dziesiąte części do dziesiątych części, setne części do setnych części itd. Jeśli któryś z ułamków ma mniej cyfr po przecinku niż inny, możemy dopisać zera na końcu, aby wyrównać liczbę cyfr po przecinku. Nie zmieni to wartości ułamka, a ułatwi obliczenia.

Przykładowo, dodajmy 3,25 i 1,7. Układamy je w słupku:

  3,25
+ 1,70
-------

Zauważ, że dopisaliśmy zero do 1,7, aby mieć dwie cyfry po przecinku, tak jak w 3,25. Teraz możemy przystąpić do dodawania, zaczynając od kolumny z prawej strony, czyli od setnych części.

Dodajemy 5 + 0, co daje 5. Zapisujemy 5 w kolumnie setnych części. Następnie przechodzimy do kolumny dziesiątych części. Dodajemy 2 + 7, co daje 9. Zapisujemy 9 w kolumnie dziesiątych części. Teraz dodajemy całości: 3 + 1, co daje 4. Zapisujemy 4 w kolumnie całości. Na koniec przepisujemy przecinek w tym samym miejscu, w którym był w dodawanych liczbach.

Otrzymujemy:

  3,25
+ 1,70
-------
  4,95

Zatem 3,25 + 1,7 = 4,95.

Kolejny przykład: dodajmy 12,4 + 0,86 + 5,003.

Układamy liczby w słupku, pamiętając o wyrównaniu przecinków:

  12,400
   0,860
+  5,003
--------

Dopisaliśmy zera, aby każdy ułamek miał trzy cyfry po przecinku. Teraz dodajemy kolumnami, zaczynając od prawej:

0 + 0 + 3 = 3 0 + 6 + 0 = 6 4 + 8 + 0 = 12 (zapisujemy 2, a 1 przenosimy do następnej kolumny) 1 (przeniesione) + 2 + 0 + 5 = 8 1 + 0 + 0 = 1

Przepisujemy przecinek i otrzymujemy:

  12,400
   0,860
+  5,003
--------
  18,263

Zatem 12,4 + 0,86 + 5,003 = 18,263.

Przejdźmy teraz do odejmowania ułamków dziesiętnych. Zasady są bardzo podobne do dodawania. Ponownie, kluczowe jest poprawne ułożenie liczb w słupku, tak aby przecinki znajdowały się w jednej linii pionowej.

Załóżmy, że chcemy odjąć 2,15 od 5,6. Układamy liczby w słupku:

  5,60
- 2,15
-------

Dopisaliśmy zero do 5,6, aby mieć dwie cyfry po przecinku, tak jak w 2,15. Teraz przystępujemy do odejmowania, zaczynając od kolumny z prawej strony, czyli od setnych części.

Odejmujemy 0 - 5. Ponieważ nie możemy odjąć 5 od 0, musimy "pożyczyć" 1 z kolumny dziesiątych części. Zatem 6 w kolumnie dziesiątych części zmniejsza się do 5, a 0 w kolumnie setnych części zmienia się na 10. Teraz możemy odjąć 10 - 5, co daje 5. Zapisujemy 5 w kolumnie setnych części.

Następnie przechodzimy do kolumny dziesiątych części. Odejmujemy 5 - 1, co daje 4. Zapisujemy 4 w kolumnie dziesiątych części. Teraz odejmujemy całości: 5 - 2, co daje 3. Zapisujemy 3 w kolumnie całości. Na koniec przepisujemy przecinek w tym samym miejscu, w którym był w odejmowanych liczbach.

Otrzymujemy:

  5,60
- 2,15
-------
  3,45

Zatem 5,6 - 2,15 = 3,45.

Kolejny przykład: odejmijmy 7,02 od 10.

Układamy liczby w słupku:

 10,00
- 7,02
-------

Dopisaliśmy przecinek i dwa zera do 10, aby mieć dwie cyfry po przecinku, tak jak w 7,02. Teraz odejmujemy kolumnami, zaczynając od prawej:

0 - 2. Musimy pożyczyć. Zaczynamy od pożyczenia od całości. 10 zmienia się na 9, a 0 w kolumnie dziesiątych części zmienia się na 10. Następnie pożyczamy od dziesiątych części – 10 zmienia się na 9, a 0 w kolumnie setnych części zmienia się na 10. Teraz możemy odjąć 10 - 2 = 8.

Następnie odejmujemy 9 - 0 = 9.

Na koniec odejmujemy 9 - 7 = 2.

Przepisujemy przecinek i otrzymujemy:

 10,00
- 7,02
-------
  2,98

Zatem 10 - 7,02 = 2,98.

Praktyczne zastosowania dodawania i odejmowania ułamków dziesiętnych

Dodawanie i odejmowanie ułamków dziesiętnych to nie tylko ćwiczenia w zeszycie. Umiejętności te są niezwykle przydatne w codziennym życiu. Oto kilka przykładów:

• Zakupy: Obliczanie łącznego kosztu zakupów, sprawdzanie, czy masz wystarczająco pieniędzy na wszystkie produkty, obliczanie reszty. Na przykład, jeśli kupujesz chleb za 3,50 zł, masło za 7,20 zł i ser za 12,85 zł, możesz dodać te kwoty, aby obliczyć łączny koszt: 3,50 + 7,20 + 12,85 = 23,55 zł.
• Gotowanie: Dostosowywanie przepisów, odmierzanie składników. Przepisy często podają ilości składników w ułamkach dziesiętnych.
• Finanse: Planowanie budżetu, obliczanie oszczędności, sprawdzanie stanu konta bankowego.
• Mierzenie: Obliczanie długości, powierzchni i objętości.
• Podróże: Obliczanie odległości, czasu podróży i kosztów paliwa. Na przykład, jeśli przejechałeś 150,7 km, a Twój samochód spala 7,5 litra paliwa na 100 km, możesz obliczyć, ile paliwa zużyłeś: (150,7 / 100) * 7,5 = 11,3025 litra.

Ćwiczenia na dodawanie i odejmowanie ułamków dziesiętnych

Aby utrwalić wiedzę, warto rozwiązać kilka przykładów. Oto kilka ćwiczeń:

1. Oblicz: 2,75 + 1,3
2. Oblicz: 8,9 - 3,45
3. Oblicz: 15,6 + 2,08 + 0,5
4. Oblicz: 20 - 6,75
5. Oblicz: 4,5 + 3,25 - 1,8

Odpowiedzi:

1. 4,05
2. 5,45
3. 18,18
4. 13,25
5. 5,95

Pamiętaj, że praktyka czyni mistrza. Im więcej będziesz ćwiczyć, tym łatwiej będzie Ci dodawać i odejmować ułamki dziesiętne. Nie zrażaj się początkowymi trudnościami. Z każdym rozwiązanym przykładem będziesz coraz pewniejszy swoich umiejętności.

Podsumowując, dodawanie i odejmowanie ułamków dziesiętnych to proste, ale bardzo ważne umiejętności. Pamiętaj o układaniu liczb w słupku z wyrównanymi przecinkami i o dopisywaniu zer, jeśli to konieczne. Ćwicz regularnie, a szybko opanujesz te zagadnienia.