Dodawanie I Odejmowanie Ułamków Dziesiętnych Klasa 4

Ułamki dziesiętne, choć na pierwszy rzut oka mogą wydawać się trudne, są bardzo praktyczne i spotykamy je na co dzień, na przykład podczas mierzenia długości, ważenia produktów czy liczenia pieniędzy. Nauka operacji na ułamkach dziesiętnych to ważny krok w matematycznej edukacji. Zaczynamy!

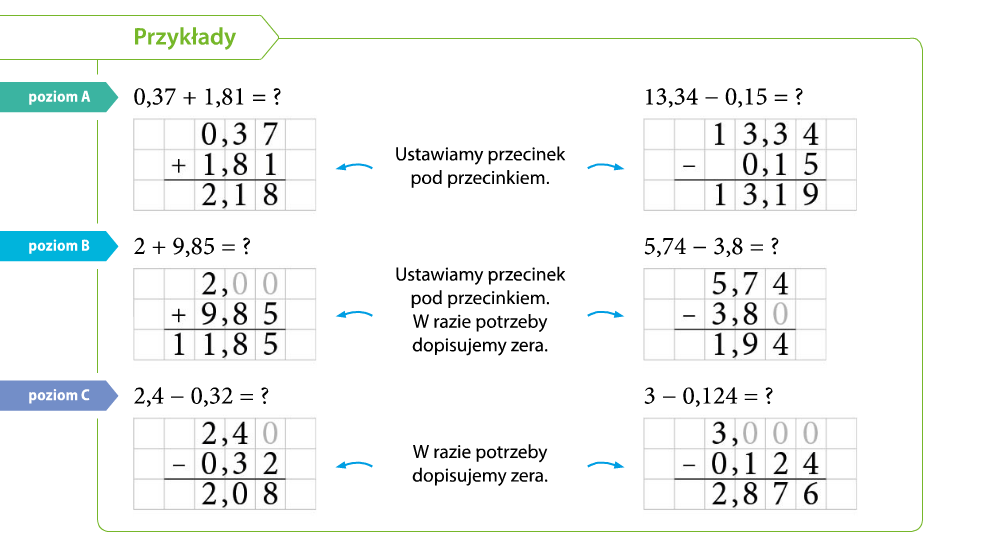
Dodawanie ułamków dziesiętnych zaczyna się od poprawnego zapisania liczb jedna pod drugą. Kluczowe jest, aby przecinki były idealnie w jednej linii pionowej. Wtedy mamy pewność, że dodajemy do siebie odpowiednie rzędy – jedności do jedności, dziesiąte części do dziesiątych części, setne części do setnych części itd.

Na przykład, chcemy dodać 3,25 i 1,42. Zapisujemy to tak:

  3,25
+ 1,42
-------

Dodajemy cyfry w każdej kolumnie, zaczynając od prawej strony, tak jak przy dodawaniu liczb całkowitych. 5 + 2 daje 7. Zapisujemy 7 pod kreską w kolumnie setnych części. 2 + 4 daje 6. Zapisujemy 6 pod kreską w kolumnie dziesiątych części. 3 + 1 daje 4. Zapisujemy 4 pod kreską w kolumnie jedności. Przecinek w wyniku stawiamy dokładnie pod przecinkami w dodawanych liczbach.

  3,25
+ 1,42
-------
  4,67

Wynik to 4,67.

A co, jeśli mamy do dodania liczby z różną ilością cyfr po przecinku? Na przykład, 2,7 + 1,35. W takim przypadku możemy dopisać zero na końcu liczby z mniejszą ilością cyfr po przecinku, aby wyrównać ilości cyfr. Zatem 2,7 zamieniamy na 2,70. To nie zmienia wartości liczby, ale ułatwia dodawanie.

  2,70
+ 1,35
-------

Teraz możemy dodać: 0 + 5 daje 5, 7 + 3 daje 10. Piszemy 0 i przenosimy 1 do kolumny jedności. 1 (przeniesione) + 2 + 1 daje 4. Zapisujemy przecinek pod przecinkami.

  2,70
+ 1,35
-------
  4,05

Wynik to 4,05.

Dodawanie większej liczby ułamków dziesiętnych działa na tej samej zasadzie. Układamy liczby tak, aby przecinki były w jednej linii, dopisujemy zera, jeśli to konieczne, i dodajemy kolumnami.

Odejmowanie ułamków dziesiętnych jest bardzo podobne do dodawania. Znowu kluczowe jest poprawne ułożenie liczb jedna pod drugą, z przecinkami w jednej linii.

Chcemy odjąć 1,23 od 4,56. Zapisujemy to tak:

  4,56
- 1,23
-------

Odejmujemy cyfry w każdej kolumnie, zaczynając od prawej strony. 6 - 3 daje 3. Zapisujemy 3 pod kreską w kolumnie setnych części. 5 - 2 daje 3. Zapisujemy 3 pod kreską w kolumnie dziesiątych części. 4 - 1 daje 3. Zapisujemy 3 pod kreską w kolumnie jedności. Przecinek w wyniku stawiamy dokładnie pod przecinkami w odejmowanych liczbach.

  4,56
- 1,23
-------
  3,33

Wynik to 3,33.

Co, jeśli mamy do odjęcia liczby z różną ilością cyfr po przecinku? Na przykład, 5,8 - 2,15. Podobnie jak przy dodawaniu, możemy dopisać zero na końcu liczby z mniejszą ilością cyfr po przecinku, aby wyrównać ilości cyfr. Zatem 5,8 zamieniamy na 5,80.

  5,80
- 2,15
-------

Teraz możemy odjąć: 0 - 5. Nie możemy odjąć 5 od 0, więc musimy "pożyczyć" 1 z kolumny dziesiątych części. 8 zamienia się na 7, a 0 zamienia się na 10. 10 - 5 daje 5. Zapisujemy 5 pod kreską w kolumnie setnych części. 7 - 1 daje 6. Zapisujemy 6 pod kreską w kolumnie dziesiątych części. 5 - 2 daje 3. Zapisujemy przecinek pod przecinkami.

  5,80
- 2,15
-------
  3,65

Wynik to 3,65.

Zadania tekstowe z ułamkami dziesiętnymi

Ułamki dziesiętne pojawiają się bardzo często w zadaniach tekstowych. Ważne jest, aby uważnie przeczytać treść zadania i zrozumieć, co trzeba zrobić – dodać czy odjąć.

Przykład: Ania kupiła jabłka za 3,50 zł i gruszki za 2,75 zł. Ile zapłaciła Ania za zakupy?

Musimy dodać ceny jabłek i gruszek. Zapisujemy to tak:

  3,50
+ 2,75
-------

Dodajemy: 0 + 5 daje 5, 5 + 7 daje 12. Piszemy 2 i przenosimy 1 do kolumny jedności. 1 (przeniesione) + 3 + 2 daje 6. Zapisujemy przecinek pod przecinkami.

  3,50
+ 2,75
-------
  6,25

Ania zapłaciła 6,25 zł.

Inny przykład: Tata ma 1,85 m wzrostu, a syn ma 1,52 m wzrostu. O ile tata jest wyższy od syna?

Musimy odjąć wzrost syna od wzrostu taty. Zapisujemy to tak:

  1,85
- 1,52
-------

Odejmujemy: 5 - 2 daje 3, 8 - 5 daje 3, 1 - 1 daje 0. Zapisujemy przecinek pod przecinkami.

  1,85
- 1,52
-------
  0,33

Tata jest wyższy od syna o 0,33 m.

Trudniejsze przykłady z zerami

Czasami musimy poradzić sobie z przykładami, które wydają się trudniejsze ze względu na zera. Na przykład, 5 - 2,35. Możemy zapisać 5 jako 5,00.

  5,00
- 2,35
-------

Teraz możemy odjąć. 0 - 5. Nie możemy odjąć 5 od 0, więc musimy pożyczyć. Pożyczamy od kolumny dziesiątych części, ale tam też jest 0. Więc musimy pożyczyć od kolumny jedności. 5 zamienia się na 4. Zero w kolumnie dziesiątych części zamienia się na 10, ale musimy pożyczyć 1 dla kolumny setnych części, więc 10 zamienia się na 9. Zero w kolumnie setnych części zamienia się na 10. Teraz możemy odjąć. 10 - 5 daje 5. 9 - 3 daje 6. 4 - 2 daje 2. Zapisujemy przecinek pod przecinkami.

  5,00
- 2,35
-------
  2,65

Wynik to 2,65.

Podsumowując, dodawanie i odejmowanie ułamków dziesiętnych wymaga przede wszystkim starannego układania liczb, wyrównywania ilości cyfr po przecinku i uważnego przeprowadzania obliczeń kolumnami. Pamiętaj o przecinku! Ćwiczenie czyni mistrza, więc rozwiązuj jak najwięcej zadań, aby nabrać wprawy.