Dodawanie I Odejmowanie Liczb Dodatnich Klasa 7 Pdf

Hej uczniowie klasy 7! Przygotowujecie się do sprawdzianu z dodawania i odejmowania liczb dodatnich? Świetnie! Zrobiłem dla was ten przewodnik, żeby pomóc wam utrwalić wiedzę i poczuć się pewnie przed testem. Traktujcie to jako nasze wspólne powtórzenie – krok po kroku, z dużą dozą zrozumienia i bez stresu!

Podstawy, czyli co musisz wiedzieć na początek

Zanim zaczniemy rozwiązywać zadania, musimy przypomnieć sobie kilka podstawowych definicji i zasad. To fundament, na którym zbudujemy całą naszą wiedzę.

Liczby dodatnie: To liczby większe od zera. Mogą być całkowite (np. 1, 2, 3, 100) lub ułamkowe (np. 0.5, 2.75, 1/4). Często zapisujemy je bez znaku, na przykład 5, ale równie dobrze możemy zapisać +5. Znak "+" pokazuje, że liczba jest dodatnia.
Dodawanie: To łączenie dwóch lub więcej liczb w jedną, zwaną sumą. Dodawanie liczb dodatnich jest proste – po prostu je sumujemy. Pamiętaj, że dodawanie jest przemienne (kolejność dodawania nie ma znaczenia, np. 3 + 5 = 5 + 3) i łączne (możemy dodawać liczby w dowolnej kolejności, np. (2 + 3) + 4 = 2 + (3 + 4)).
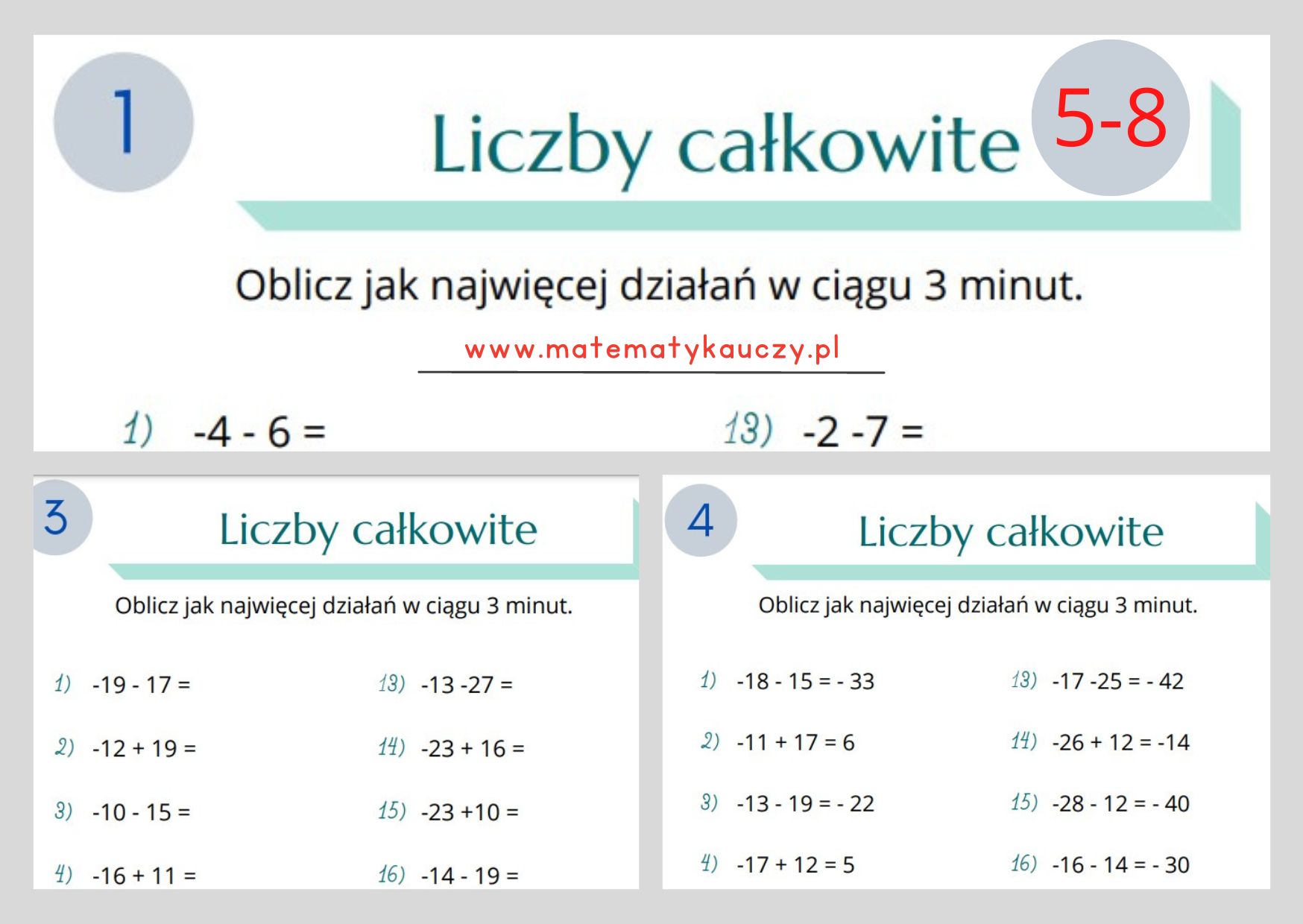
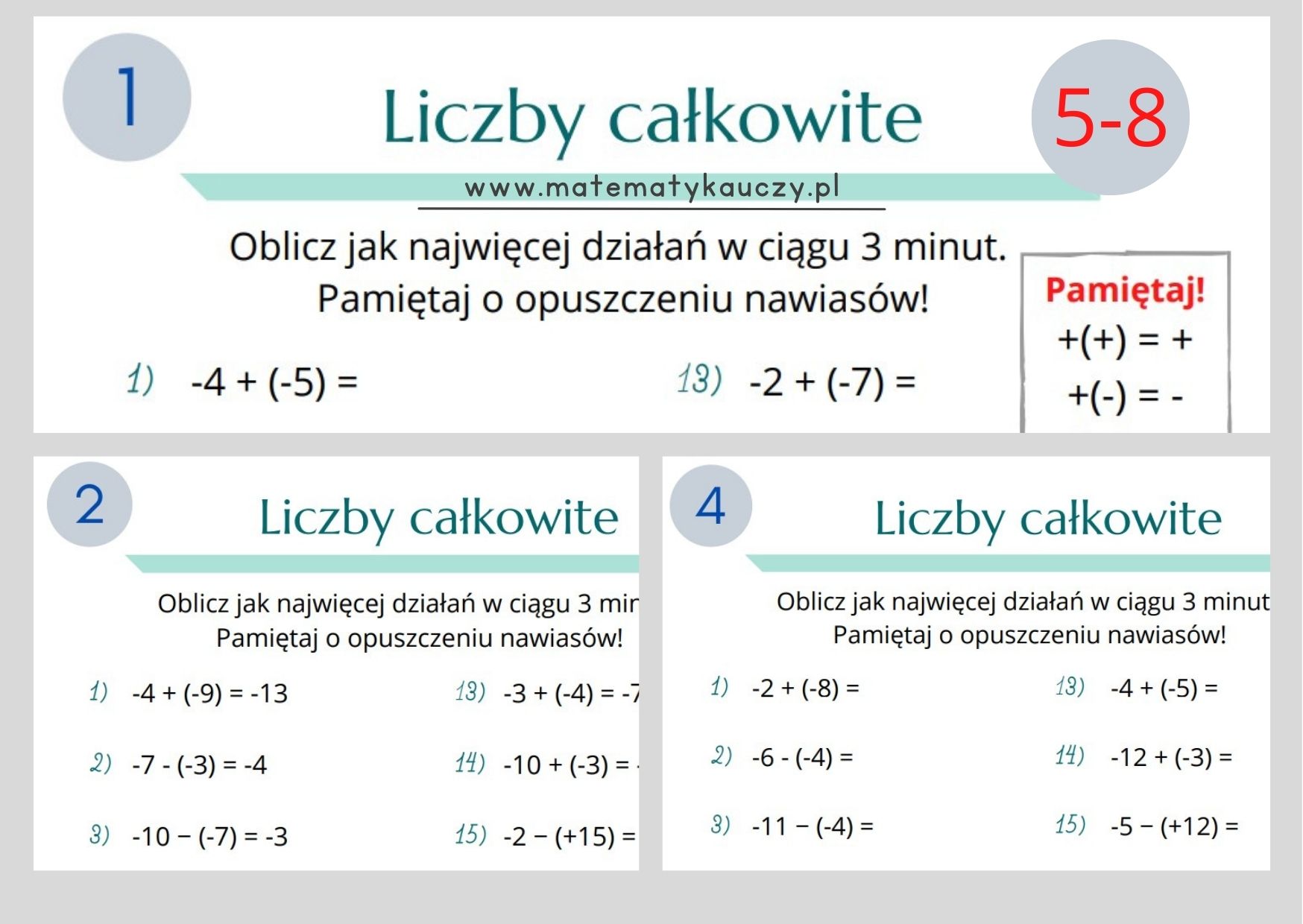
Odejmowanie: To proces znajdowania różnicy między dwiema liczbami. Liczba, od której odejmujemy, nazywana jest odjemną, a liczba, którą odejmujemy, nazywana jest odjemnikiem. Wynik odejmowania to różnica. Odejmowanie NIE jest przemienne (5 - 3 ≠ 3 - 5).
Działania pisemne: Szczególnie przy większych liczbach, warto przypomnieć sobie pisemne dodawanie i odejmowanie. Upewnij się, że dobrze układasz liczby w kolumnach (jedności pod jednościami, dziesiątki pod dziesiątkami, itd.) i pamiętaj o przenoszeniu i pożyczaniu.

Dodawanie liczb dodatnich – krok po kroku

Dodawanie liczb dodatnich to, tak jak wspomniałem, dość prosta sprawa. Przećwiczmy to na kilku przykładach:

Przykład 1: Dodawanie liczb całkowitych

Oblicz: 123 + 45 + 6

Możemy dodać te liczby w dowolnej kolejności. Zacznijmy od 123 + 45. Daje nam to 168. Następnie dodajemy 6: 168 + 6 = 174.

Odpowiedź: 123 + 45 + 6 = 174
Przykład 2: Dodawanie liczb ułamkowych (dziesiętnych)

Oblicz: 2.5 + 3.75 + 0.2

Tutaj ważne jest, żeby pamiętać o wyrównaniu przecinków. Możemy zapisać to tak:

2,50
- 3,75
- 0,20
6,45

Zauważ, że dodałem zero na końcu 2,5 i 0,2, żeby wyrównać ilość miejsc po przecinku.

Odpowiedź: 2.5 + 3.75 + 0.2 = 6.45
Przykład 3: Dodawanie ułamków zwykłych

Oblicz: 1/2 + 1/4

Żeby dodać ułamki zwykłe, musimy sprowadzić je do wspólnego mianownika. W tym przypadku wspólnym mianownikiem będzie 4.

1/2 = 2/4 (pomnożyliśmy licznik i mianownik przez 2)

Teraz możemy dodać: 2/4 + 1/4 = 3/4

Odpowiedź: 1/2 + 1/4 = 3/4

Odejmowanie liczb dodatnich – na co zwrócić uwagę

Odejmowanie, choć wydaje się równie proste, wymaga trochę więcej uwagi. Pamiętajmy o kolejności wykonywania działań i o tym, co się dzieje, gdy od mniejszej liczby odejmujemy większą. (W tym przypadku, skupiamy się tylko na dodatnich wynikach, więc zawsze będziemy odejmować mniejszą liczbę od większej).

Przykład 1: Odejmowanie liczb całkowitych

Oblicz: 56 - 23

To proste odejmowanie pisemne.

56
- 23
33

Odpowiedź: 56 - 23 = 33
Przykład 2: Odejmowanie liczb ułamkowych (dziesiętnych)

Oblicz: 7.85 - 3.1

Podobnie jak przy dodawaniu, wyrównujemy przecinki:

7,85
- 3,10
4,75

Odpowiedź: 7.85 - 3.1 = 4.75
Przykład 3: Odejmowanie ułamków zwykłych

Oblicz: 3/4 - 1/2

Znowu, sprowadzamy do wspólnego mianownika, którym jest 4.

1/2 = 2/4

Teraz możemy odjąć: 3/4 - 2/4 = 1/4

Odpowiedź: 3/4 - 1/2 = 1/4

Kiedy pojawiają się "schody" – typowe błędy i jak ich unikać

Wiem, że czasami zdarzają się pomyłki, ale spokojnie, każdy je robi! Ważne, żeby się na nich uczyć. Oto kilka typowych błędów i sposobów na ich uniknięcie:

Błąd w układaniu liczb w kolumnach (przy dodawaniu i odejmowaniu pisemnym): Zawsze upewnij się, że jedności są pod jednościami, dziesiątki pod dziesiątkami, setne pod setnymi itd. To podstawa!
Zapominanie o przenoszeniu i pożyczaniu (przy dodawaniu i odejmowaniu pisemnym): To częsty błąd. Zawsze sprawdzaj, czy musisz coś przenieść lub pożyczyć. Możesz zaznaczać małe cyfry na górze, żeby o tym pamiętać.
Błędne sprowadzanie ułamków do wspólnego mianownika: Upewnij się, że dobrze mnożysz zarówno licznik, jak i mianownik. Jeśli masz problem, spróbuj rozpisać sobie, przez co mnożysz każdy ułamek.
Pomylenie kolejności w odejmowaniu: Pamiętaj, że odejmowanie NIE jest przemienne! Zawsze odejmuj odjemnik od odjemnej.
Błędy w obliczeniach – pośpiech: Najczęstszym powodem pomyłek jest pośpiech. Lepiej rozwiązywać wolniej, ale dokładniej. Sprawdzaj swoje obliczenia!

Triki i sztuczki, które ułatwią ci życie

Oto kilka dodatkowych wskazówek, które mogą ci się przydać:

Zaokrąglanie: Jeśli masz skomplikowane liczby dziesiętne, możesz je zaokrąglić do najbliższej liczby całkowitej lub do jednego miejsca po przecinku, żeby oszacować wynik. Potem możesz wrócić do dokładnych obliczeń.
Rozkładanie liczb: Czasami łatwiej jest dodać lub odjąć liczby, jeśli rozłożysz je na mniejsze części. Na przykład: 17 + 8 = (10 + 7) + 8 = 10 + (7 + 8) = 10 + 15 = 25
Używaj szacowania: Przed rozwiązaniem zadania, spróbuj oszacować wynik. To pomoże ci zorientować się, czy twoja odpowiedź jest sensowna. Na przykład, jeśli masz dodać 48 + 52, to wiesz, że wynik powinien być bliski 100.

H2 Przykładowe zadania z rozwiązaniami

Teraz przejdźmy do konkretnych zadań, żeby zobaczyć, jak to wszystko wygląda w praktyce.

Zadanie 1:

Tata kupił owoce: 2 kg jabłek po 3.50 zł za kg, 1.5 kg gruszek po 4.20 zł za kg i 0.75 kg śliwek po 5 zł za kg. Ile tata zapłacił za owoce?
- Rozwiązanie:
  - Koszt jabłek: 2 kg * 3.50 zł/kg = 7 zł
  - Koszt gruszek: 1.5 kg * 4.20 zł/kg = 6.30 zł
  - Koszt śliwek: 0.75 kg * 5 zł/kg = 3.75 zł
  - Całkowity koszt: 7 zł + 6.30 zł + 3.75 zł = 17.05 zł
  Odpowiedź: Tata zapłacił 17.05 zł za owoce.
Zadanie 2:

Mama upiekła ciasto i pokroiła je na 12 kawałków. Kasia zjadła 1/3 ciasta, a Tomek 1/4 ciasta. Ile kawałków ciasta zostało?
- Rozwiązanie:
  - Kasia zjadła: 1/3 * 12 = 4 kawałki
  - Tomek zjadł: 1/4 * 12 = 3 kawałki
  - Razem zjedli: 4 + 3 = 7 kawałków
  - Zostało: 12 - 7 = 5 kawałków
  Odpowiedź: Zostało 5 kawałków ciasta.
Zadanie 3:

W klasie jest 25 uczniów. 1/5 uczniów lubi matematykę, a 2/5 uczniów lubi język polski. Ilu uczniów lubi matematykę, a ilu język polski?
- Rozwiązanie:
  - Liczba uczniów lubiących matematykę: 1/5 * 25 = 5 uczniów
  - Liczba uczniów lubiących język polski: 2/5 * 25 = 10 uczniów
  Odpowiedź: Matematykę lubi 5 uczniów, a język polski lubi 10 uczniów.

H2 Co robić, jeśli nadal masz problemy?

Nie martw się, jeśli coś ci jeszcze sprawia trudność! To normalne. Oto kilka rad:

Zapytaj nauczyciela: Nauczyciel jest po to, żeby ci pomóc. Nie wstydź się zadawać pytań!
Poproś o pomoc kolegę/koleżankę: Czasami tłumaczenie od kogoś, kto to rozumie, może być bardzo pomocne.
Poszukaj dodatkowych materiałów: W Internecie jest mnóstwo materiałów edukacyjnych, filmów, ćwiczeń. Wykorzystaj je! (Pamiętaj tylko o wiarygodnych źródłach).
Rozwiązuj więcej zadań: Praktyka czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz dany temat.

Podsumowanie – kluczowe punkty

Liczby dodatnie: Liczby większe od zera.
Dodawanie: Łączenie liczb w sumę (przemienne i łączne).
Odejmowanie: Znajdowanie różnicy (NIE jest przemienne!).
Ułamki: Pamiętaj o sprowadzaniu do wspólnego mianownika.
Działania pisemne: Układaj liczby w kolumnach, pamiętaj o przenoszeniu i pożyczaniu.
Sprawdzaj: Zawsze sprawdzaj swoje obliczenia!

Pamiętajcie, że najważniejsze to ćwiczyć i nie poddawać się! Wierzę w was! Powodzenia na sprawdzianie! Jesteście świetni i na pewno dacie radę!