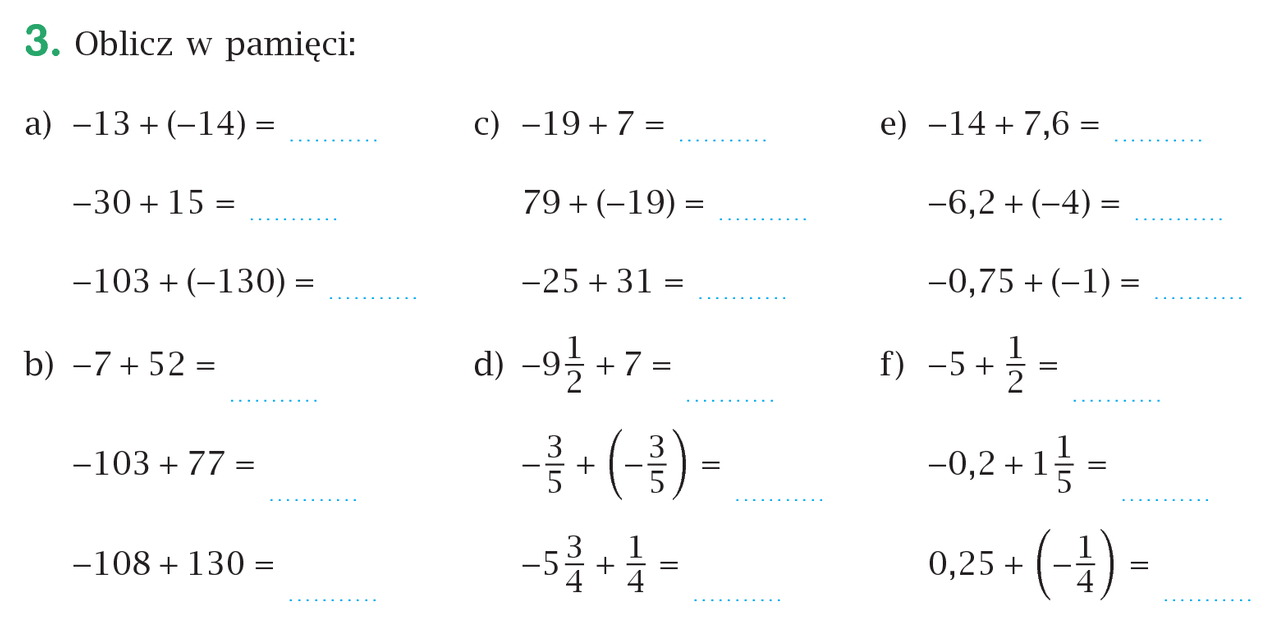Dodawanie I Odejmowanie Liczb Całkowitych Klasa 6 Zadania

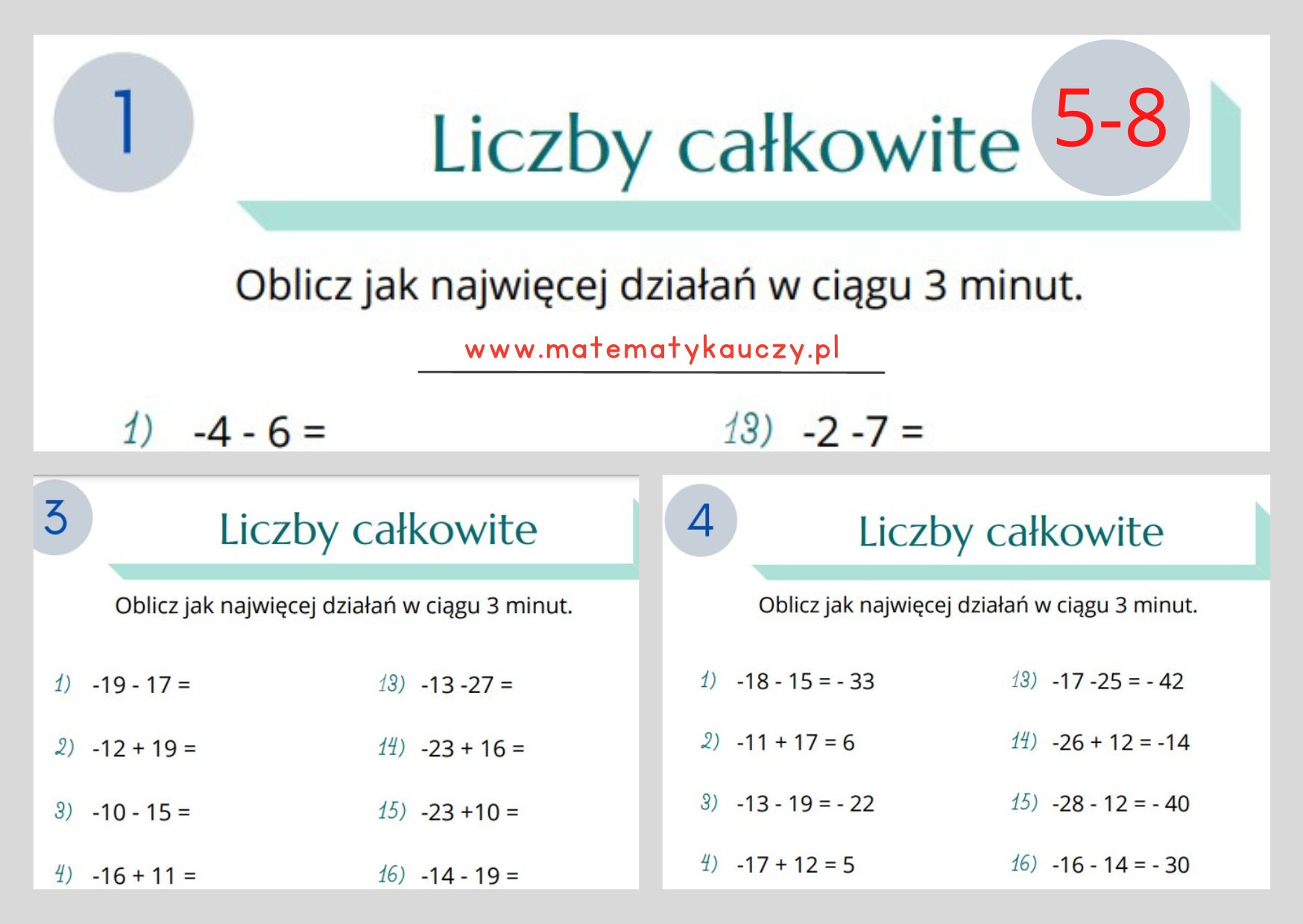
Dobrze, moi drodzy uczniowie! Widzę, że macie pytania dotyczące dodawania i odejmowania liczb całkowitych. To temat, który na początku może wydawać się trochę zagmatwany, ale spokojnie, wszystko da się wytłumaczyć! Postaram się odpowiedzieć na wasze pytania jak najprościej i najjaśniej.

Zacznijmy od podstaw. Liczby całkowite to takie liczby, które nie mają żadnej części ułamkowej. Czyli na przykład... 1, 2, 3, 0, -1, -2, -3 i tak dalej. Wszystkie te "całe" liczby. Ważne jest, że mogą być dodatnie (te zwykłe, które znamy od dawna), ujemne (z minusem przed) i zero.

Dodawanie Liczb Całkowitych

Wyobraźmy sobie, że mamy dwie grupy liczb całkowitych, które chcemy połączyć. Tutaj najważniejsze są znaki, czyli plusy i minusy.

Dodawanie liczb o tym samym znaku:
- Jeżeli dodajemy dwie liczby dodatnie, to sprawa jest prosta. Robimy to tak, jak zawsze. Na przykład: 2 + 3 = 5. No problem!
- Jeżeli dodajemy dwie liczby ujemne, to dodajemy ich wartości bezwzględne (czyli ignorujemy minusy), a na końcu dopisujemy minus. Na przykład: (-2) + (-3) = -5. Po prostu dodajemy 2 i 3, co daje 5, a potem dodajemy minusa.
Dodawanie liczb o różnych znakach:
- Tutaj musimy pomyśleć trochę bardziej. Odejmujemy mniejszą wartość bezwzględną od większej wartości bezwzględnej. A potem patrzymy, która z tych liczb (bez znaku) była większa i taki znak wstawiamy do wyniku.
- Na przykład: (-5) + 2. Wartość bezwzględna z -5 to 5, a wartość bezwzględna z 2 to 2. Odejmujemy 2 od 5, co daje nam 3. Ponieważ 5 (bez znaku) było większe i miało minus, to wynik będzie -3. Czyli (-5) + 2 = -3.
- Inny przykład: 7 + (-3). Wartość bezwzględna z 7 to 7, a wartość bezwzględna z -3 to 3. Odejmujemy 3 od 7, co daje nam 4. Ponieważ 7 (bez znaku) było większe i miało plus (którego nie piszemy), to wynik będzie 4. Czyli 7 + (-3) = 4.

Odejmowanie Liczb Całkowitych

Odejmowanie jest bardzo podobne do dodawania, tylko musimy pamiętać o jednej bardzo ważnej rzeczy: odejmowanie możemy zamienić na dodawanie liczby przeciwnej. Co to znaczy?

Liczba przeciwna do 5 to -5, a liczba przeciwna do -3 to 3. Po prostu zmieniamy znak.

Teraz, żeby odjąć dwie liczby, zamieniamy odejmowanie na dodawanie liczby przeciwnej.

Na przykład: 5 - 3. Możemy to zapisać jako 5 + (-3). A to już wiemy jak policzyć! Wartość bezwzględna z 5 to 5, a wartość bezwzględna z -3 to 3. Odejmujemy 3 od 5, co daje nam 2. Ponieważ 5 (bez znaku) było większe i miało plus, to wynik będzie 2. Czyli 5 - 3 = 2.
Inny przykład: 2 - 5. Zamieniamy na 2 + (-5). Wartość bezwzględna z 2 to 2, a wartość bezwzględna z -5 to 5. Odejmujemy 2 od 5, co daje nam 3. Ponieważ 5 (bez znaku) było większe i miało minus, to wynik będzie -3. Czyli 2 - 5 = -3.
Co jeśli odejmujemy liczbę ujemną? Na przykład: 4 - (-2). Zamieniamy na 4 + 2. A to już jest proste dodawanie! 4 + 2 = 6.

Kilka Dodatkowych Wskazówek i Przykładów

Pamiętajcie, że kolejność wykonywania działań jest ważna. Najpierw nawiasy, potem mnożenie i dzielenie, a na końcu dodawanie i odejmowanie.
Zwracajcie uwagę na znaki. Jeden mały błąd i wynik może być zupełnie inny!
Ćwiczcie, ćwiczcie, ćwiczcie! Im więcej zadań rozwiążecie, tym łatwiej Wam to będzie przychodziło.
Wyobraźcie sobie oś liczbową. Dodawanie liczby dodatniej to poruszanie się w prawo, a dodawanie liczby ujemnej to poruszanie się w lewo. Odejmowanie liczby dodatniej to poruszanie się w lewo, a odejmowanie liczby ujemnej to poruszanie się w prawo. To może pomóc Wam wizualizować te operacje.

Przykłady:

(-8) + 5 = -3
12 + (-4) = 8
(-6) + (-9) = -15
3 - 7 = 3 + (-7) = -4
-2 - 4 = -2 + (-4) = -6
5 - (-3) = 5 + 3 = 8
-4 - (-1) = -4 + 1 = -3

Spróbujmy jeszcze kilka bardziej złożonych przykładów:

(2 + (-5)) - 3 = (-3) - 3 = (-3) + (-3) = -6
-7 - (4 + (-2)) = -7 - (2) = -7 + (-2) = -9
-10 + (8 - (-1)) = -10 + (8 + 1) = -10 + 9 = -1
(5 - 9) + (-2 + 6) = (-4) + (4) = 0

Mam nadzieję, że to wyjaśnienie pomogło Wam zrozumieć dodawanie i odejmowanie liczb całkowitych. Jeżeli macie jeszcze jakieś pytania, śmiało pytajcie! Pamiętajcie, praktyka czyni mistrza! Spróbujcie rozwiązać jak najwięcej zadań, a z pewnością wszystko stanie się dla Was jasne i proste. Nie bójcie się popełniać błędów, bo na błędach się uczymy. Powodzenia!