Do Narysowania Wykresu Funkcji Liniowej Najlepiej Zastosować Wykres

Dobrze, posłuchajcie uważnie. Kiedy stajemy przed zadaniem narysowania wykresu funkcji liniowej, najważniejszą rzeczą jest zrozumienie, że nie stosujemy wykresu do narysowania wykresu. Wykorzystujemy do tego szereg technik i narzędzi, a sam wykres jest rezultatem naszej pracy, a nie punktem wyjścia.

Funkcja liniowa, jak doskonale wiecie, ma postać f(x) = ax + b, gdzie a to współczynnik kierunkowy, a b to wyraz wolny. Te dwa parametry determinują całą charakterystykę funkcji i sposób, w jaki przedstawia się ona na płaszczyźnie kartezjańskiej.

Najpierw musimy zidentyfikować współczynniki a i b. Odczytujemy je bezpośrednio z równania funkcji. To one stanowią klucz do odblokowania możliwości graficznego przedstawienia tej funkcji.

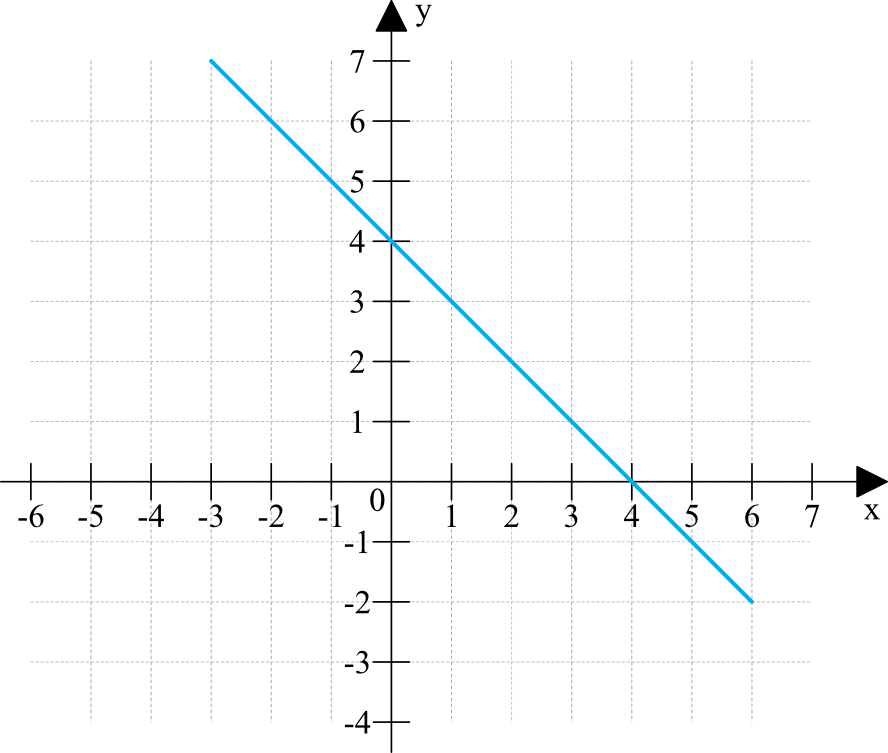
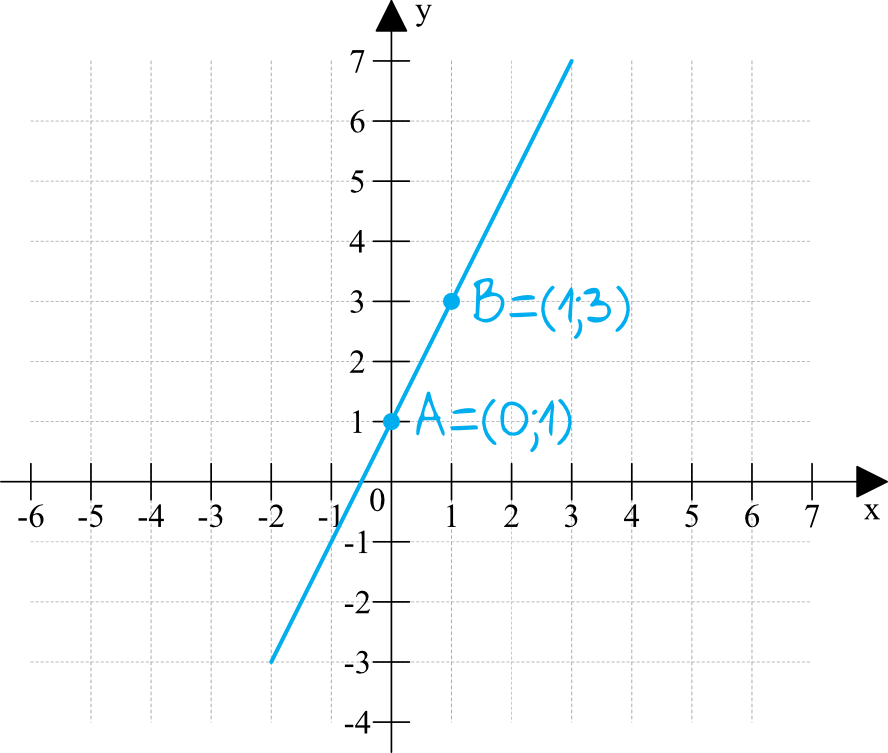
Następnie obliczamy dwa punkty należące do wykresu. Nie potrzebujemy ich więcej do narysowania linii prostej. Najprościej jest wybrać x = 0 i x = 1. Dla x = 0 otrzymujemy f(0) = a * 0 + b = b. Zatem punkt (0, b) leży na wykresie. Dla x = 1 otrzymujemy f(1) = a * 1 + b = a + b. Zatem punkt (1, a + b) również leży na wykresie. Mając te dwa punkty, mamy już wszystko, czego potrzebujemy.

Znaznaczamy oba punkty w układzie współrzędnych. Używamy linijki, aby połączyć te dwa punkty linią prostą. Linia ta jest właśnie wykresem naszej funkcji liniowej f(x) = ax + b.

Pamiętajcie, żeby przedłużyć narysowaną linię poza zaznaczone punkty, aby pokazać, że funkcja rozciąga się w nieskończoność w obie strony. To istotny element poprawnego rysunku.

Ważne jest również zaznaczenie osi układu współrzędnych, opisanie ich (oś x i oś y) oraz dodanie strzałek na końcach osi, aby wskazać kierunek wzrostu wartości. Czasami wymagane jest również dodanie skali na osiach, aby precyzyjnie odzwierciedlić położenie punktów.

Alternatywną metodą jest wykorzystanie współczynnika kierunkowego a. Pokazuje on, o ile zmienia się wartość funkcji f(x), gdy x wzrasta o 1. Zaczynamy od punktu (0, b), który zawsze leży na wykresie (jest to punkt przecięcia wykresu z osią Y). Następnie, przesuwamy się o 1 jednostkę w prawo (wzdłuż osi X) i o a jednostek w górę (jeśli a jest dodatnie) lub w dół (jeśli a jest ujemne). W ten sposób otrzymujemy drugi punkt na wykresie. Łączymy go z punktem (0, b) linią prostą i gotowe!

Jeżeli a jest ułamkiem, na przykład a = p/q, to przesuwamy się o q jednostek w prawo i o p jednostek w górę (lub w dół, w zależności od znaku p). To pozwala uniknąć rysowania z dużą niedokładnością ułamkowych przesunięć.

Pamiętajcie również o analizie znaku współczynnika a. Jeśli a > 0, funkcja jest rosnąca. Jeśli a < 0, funkcja jest malejąca. Jeśli a = 0, funkcja jest stała i jej wykresem jest linia pozioma. To dodatkowa wskazówka, pozwalająca zweryfikować poprawność narysowanego wykresu.

Bardzo ważne jest, aby rysunek był czytelny i estetyczny. Używajcie linijki, aby proste były naprawdę proste. Unikajcie rysowania na brudnym lub pogniecionym papierze. Starannie zaznaczajcie punkty i opisujcie osie. Estetyka rysunku również ma znaczenie!

Należy także pamiętać o interpretacji wykresu funkcji liniowej w kontekście konkretnego problemu. Funkcje liniowe często opisują zależności liniowe między różnymi wielkościami fizycznymi, ekonomicznymi lub społecznymi. Przykładowo, mogą reprezentować zależność kosztów od liczby wyprodukowanych przedmiotów, zależność drogi od czasu w ruchu jednostajnym, czy zależność temperatury od czasu w procesie nagrzewania.

Dlatego, rysując wykres funkcji liniowej, warto zastanowić się, co reprezentują osie X i Y w danym problemie. Jakie jednostki są używane? Co oznacza punkt przecięcia wykresu z osiami? Co oznacza nachylenie wykresu? Odpowiedzi na te pytania pozwalają zrozumieć sens fizyczny lub ekonomiczny danej zależności liniowej.

Na przykład, jeśli funkcja liniowa opisuje zależność kosztów K od liczby wyprodukowanych przedmiotów x, to punkt przecięcia wykresu z osią Y (czyli punkt (0, b)) oznacza koszty stałe, niezależne od liczby wyprodukowanych przedmiotów. Współczynnik kierunkowy a oznacza koszt jednostkowy, czyli koszt wyprodukowania jednego dodatkowego przedmiotu. Nachylenie wykresu (czyli wartość a) informuje nas, o ile wzrosną koszty, jeśli zwiększymy produkcję o jedną jednostkę.

Podobnie, jeśli funkcja liniowa opisuje zależność drogi s od czasu t w ruchu jednostajnym, to współczynnik kierunkowy a oznacza prędkość, z jaką porusza się ciało. Punkt przecięcia wykresu z osią Y (czyli punkt (0, b)) oznacza początkowe położenie ciała w momencie t = 0.

Zatem, interpretacja wykresu funkcji liniowej w kontekście danego problemu pozwala na wyciąganie wniosków i przewidywanie zachowania się opisywanego układu.

Uważaj na pułapki

Pamiętajcie, że funkcja liniowa jest zdefiniowana dla wszystkich liczb rzeczywistych. To oznacza, że jej wykres rozciąga się w nieskończoność w obie strony. Częstym błędem jest rysowanie wykresu tylko w pewnym ograniczonym zakresie, na przykład od x = 0 do x = 5. Należy pamiętać o przedłużeniu linii prostej poza zaznaczone punkty, aby pokazać, że funkcja jest zdefiniowana dla wszystkich x.

Innym częstym błędem jest pomylenie współczynnika kierunkowego a z wyrazem wolnym b. Pamiętajcie, że b to wartość funkcji dla x = 0, czyli punkt przecięcia wykresu z osią Y. Natomiast a to nachylenie wykresu, czyli zmiana wartości funkcji na jednostkę zmiany x.

Uważajcie również na znaki współczynników a i b. Zły znak może całkowicie zmienić charakter wykresu. Pamiętajcie, że jeśli a > 0, funkcja jest rosnąca, a jeśli a < 0, funkcja jest malejąca. Jeśli b > 0, wykres przecina oś Y powyżej osi X, a jeśli b < 0, wykres przecina oś Y poniżej osi X.

Unikajcie rysowania wykresów "z pamięci". Zawsze najpierw obliczcie współczynniki a i b, a następnie wyznaczcie dwa punkty na wykresie. To pozwoli uniknąć błędów i zapewni poprawność rysunku.

Dodatkowe wskazówki

Do rysowania wykresów funkcji liniowych można używać różnych narzędzi, takich jak oprogramowanie graficzne (np. GeoGebra, Desmos) lub kalkulatory graficzne. Te narzędzia pozwalają na szybkie i precyzyjne narysowanie wykresu, a także na eksperymentowanie z różnymi wartościami współczynników a i b.

Warto również ćwiczyć rysowanie wykresów funkcji liniowych na papierze. To pozwala na lepsze zrozumienie zależności między równaniem funkcji a jej graficzną reprezentacją.

Podczas rysowania wykresów funkcji liniowych warto korzystać z papieru kratkowanego. Ułatwia to precyzyjne zaznaczanie punktów i rysowanie linii prostych.

Pamiętajcie, że praktyka czyni mistrza. Im więcej wykresów funkcji liniowych narysujecie, tym lepiej będziecie rozumieć ich charakterystykę i tym łatwiej będziecie je rysować.

I na koniec, nie bójcie się pytać! Jeśli macie jakiekolwiek wątpliwości, pytajcie nauczyciela lub kolegów. Wspólna praca i dyskusja pomagają w lepszym zrozumieniu materiału. Pamiętajcie, że nauka to proces, który wymaga czasu i wysiłku. Nie zrażajcie się trudnościami, tylko dążcie do celu!